本文探讨了基于30项特征预测二手车交易价格的方法，包括数据预处理、缺失值处理、异常值检测与处理、特征工程及可视化分析。通过Pandas、Matplotlib和Seaborn等工具，对数据进行了深入分析。
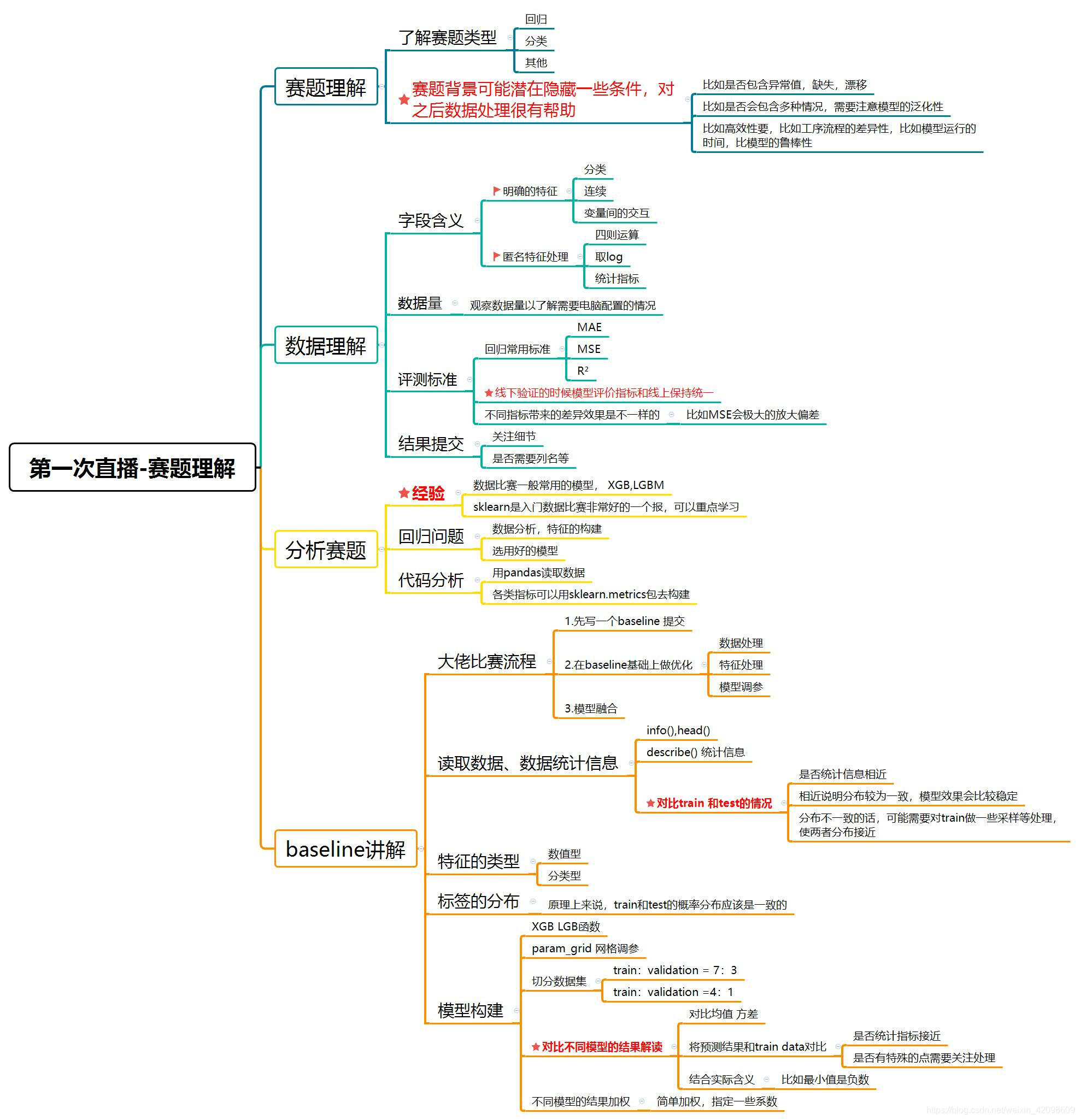
二手车交易价格预测
赛题理解
根据二手车的各项指标，预测二手车交易时的价格，典型的回归问题。给定的特征共有30个。
数据分析用到的相关包
训练集包含150000样本，测试集包含50000样本。
Pandas
Pandas可以用来读取数据，并对数据进行处理。
首先对训练集进行缺失值处理。
Pandas里读取数据得到DataFrame之后，可以用以下这条语句来检查DataFrame中是否存在Null值。
DataFrame.isnull().sum().sort_values(params)
这里介绍一下sort_values()函数的具体参数。
DataFrame.sort_values(by="##",axis=0,ascending=True,inplace=False,na_position)
- by：指定列名（axis=0或’index’）或索引值（axis=1或’columns’）
- axis：若axis=0或’index’，则按照指定列中数据大小排序；若axis=1或’columns’，则按照指定索引中数据大小排序，默认axis=0
- ascending：是否按指定列的数组升序排列，默认为True，即升序排列
- inplace：是否用排序后的数据集替换原来的数据，默认为False，即不替换
- na_position：{‘first’,‘last’}，设定缺失值的显示位置
matplotlib
matplotlib画图包，数据分析时可对数据进行可视化。
通常会用以下语句来设置图像显示的大小：
plt.figure(figsize=(a,b))
a，b分别为图像的宽和高，单位为英寸。
还有以下语法：
fig, ax = plt.subplots(1,1)
ax2 = ax.twinx() # 合并两个图的x轴
x1 = np.linspace(0,2*np.pi,100)
y1 = np.sin(x1)
ax.plot(x1,y1)
x2 = np.linspace(0,2*np.pi,100)
y2 = np.cos(x2)
ax2.plot(x2,y2)
plt.show()
seaborn
seaborn可用来绘制数据分布。
摘自链接Seaborn5分钟入门
seaborn.distplot(a, bins=None, hist=True, kde=True, rug=False, fit=None, hist_kws=None, kde_kws=None, rug_kws=None, fit_kws=None, color=None, vertical=False, norm_hist=False, axlabel=None, label=None, ax=None)
- bins：int或list，控制直方图的划分
- hist和kde参数调节是否显示直方图及核密度估计(默认hist,kde均为True)
- rag：控制是否生成观测数值的小细条
- fit：控制拟合的参数分布图形，能够直观地评估它与观察数据的对应关系(黑色线条为确定的分布)
- hist_kws, kde_kws, rug_kws, fit_kws参数接收字典类型，可以自行定义更多高级的样式
- norm_hist：若为True, 则直方图高度显示密度而非计数(含有kde图像中默认为True)
分析数据
首先查看我们需要预测的值价格“price”。
Train_data['price'].describe()
# output
count 150000.000000
mean 5923.327333
std 7501.998477
min 11.000000
25% 1300.000000
50% 3250.000000
75% 7700.000000
max 99999.000000
Name: price, dtype: float64
可以看出平均成交价格在5923左右，方差为7501左右。最低成交价格为11，最高价格为99999，这个数字有些异常，后续应该需要处理。
Train_data['price'].value_counts()
# output
500 2337
1500 2158
1200 1922
1000 1850
...
8801 1
37920 1
8188 1
Name: price, Length: 3763, dtype: int64
DataFrame[‘feature’].value_counts()是查看DataFrame在feature这一列中有多少个不同值，并计算每个不同值在该列中有多少重复值。
Train_data[Train_data['price']==99999].index.tolist()
# output
[69133, 85893, 88326, 125413, 132588]
价格为99999这样的异常值有5个。
删除价格异常的值并充值索引。
Train_data.drop(index=Ind,inplace=True)
Train_data = Train_data.reset_index(drop=True)
利用seaborn画出price的近似分布，看看price最符合哪种分布。
import scipy.stats as st
y = Train_data['price']
plt.figure(1); plt.title('Johnson SU')
sns.distplot(y,kde=False,fit=st.johnsonsu)
plt.figure(2); plt.title('Normal')
sns.distplot(y,kde=False,fit=st.norm)
plt.figure(3); plt.title('Log Normal')
sns.distplot(y,kde=False,fit=st.lognorm)
由图可以看出，价格的最佳拟合为无界约翰逊分布，只有在部分范围内，有服从正态分布的趋势，因此在将价格作为label时，需要将数据转化为服从正态分布。（当标签服从正态分布，预测值就越准确。why？）
# 查看价格的偏度与峰度
# sns.distplot(Train_data['price'])
print('skewness:',Train_data['price'].skew())
print('kurtosis:',Train_data['price'].kurt())
# output
skewness: 3.3079218530873327
kurtosis: 18.399399372309134
偏度skewness：正态分布偏度为0，右偏分布（正偏分布）大于0，左偏分布（负偏分布）小于0。
峰度kurtosis：正态分布峰度为3，厚尾峰度大于3，瘦尾峰度小于3。
偏度与峰度越接近正态分布越好。
之后需要将price转化为正态分布，如何转化？
接下来我们分析特征。
首先查看每个特征的类型。
## 通过 .info() 简要可以看到对应一些数据列名，以及NAN缺失信息
Train_data.info()
# output
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 149995 entries, 0 to 149994
Data columns (total 31 columns):
SaleID 149995 non-null int64
name 149995 non-null int64
regDate 149995 non-null int64
model 149994 non-null float64
brand 149995 non-null int64
bodyType 145491 non-null float64
fuelType 141318 non-null float64
gearbox 144017 non-null float64
power 149995 non-null int64
kilometer 149995 non-null float64
notRepairedDamage 149995 non-null object
regionCode 149995 non-null int64
seller 149995 non-null int64
offerType 149995 non-null int64
creatDate 149995 non-null int64
price 149995 non-null int64
v_0 149995 non-null float64
v_1 149995 non-null float64
v_2 149995 non-null float64
v_3 149995 non-null float64
v_4 149995 non-null float64
v_5 149995 non-null float64
v_6 149995 non-null float64
v_7 149995 non-null float64
v_8 149995 non-null float64
v_9 149995 non-null float64
v_10 149995 non-null float64
v_11 149995 non-null float64
v_12 149995 non-null float64
v_13 149995 non-null float64
v_14 149995 non-null float64
dtypes: float64(20), int64(10), object(1)
memory usage: 35.5+ MB
由输出结果可知，只有notRepairedDamage这个特征的类别为object。
查看特征缺省值。
Train_data.isnull().sum()
# output
SaleID 0
name 0
regDate 0
model 1
brand 0
bodyType 4504
fuelType 8677
gearbox 5978
power 0
kilometer 0
notRepairedDamage 0
regionCode 0
seller 0
offerType 0
creatDate 0
price 0
v_0 0
v_1 0
v_2 0
v_3 0
v_4 0
v_5 0
v_6 0
v_7 0
v_8 0
v_9 0
v_10 0
v_11 0
v_12 0
v_13 0
v_14 0
dtype: int64
model, bodyType, fuelType, gearbox分别缺失1，4504，8677，5978个值。
检查notRepairedDamage这个特征的值。
Train_data['notRepairedDamage'].value_counts()
# output
0.0 111360
- 24322
1.0 14313
Name: notRepairedDamage, dtype: int64
修改notRepairedDamage里的’-'为Nan值。
Train_data['notRepairedDamage'].replace('-',np.nan,inplace=True)
特征中包含数值特征和类型特征，将两者分开了，并统计数值变量之间的相关性。
numeric_features = ['power', 'kilometer', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13','v_14' ]
categorical_features = ['name', 'model', 'brand', 'bodyType', 'fuelType', 'gearbox', 'notRepairedDamage', 'regionCode']
# 统计数值类型相关变量
numeric_features.append('price')
price_numeric = Train_data[numeric_features]
correlation = price_numeric.corr()
f,ax = plt.subplots(figsize=(7,7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sns.heatmap(correlation,square=True,vmax=0.8)
统计特征的偏度和峰度
#查看特征值的偏度和峰度
for col in numeric_features:
print('{:15}'.format(col),
'skewness:{:05.2f}'.format(Train_data[col].skew()),
'kurtosis:{:06.2f}'.format(Train_data[col].kurt()))
# output
power skewness:65.86 kurtosis:5733.47
kilometer skewness:-1.53 kurtosis:001.14
v_0 skewness:-1.32 kurtosis:003.99
v_1 skewness:00.36 kurtosis:-01.75
v_2 skewness:04.84 kurtosis:023.87
v_3 skewness:00.11 kurtosis:-00.42
v_4 skewness:00.37 kurtosis:-00.20
v_5 skewness:-4.74 kurtosis:022.94
v_6 skewness:00.37 kurtosis:-01.74
v_7 skewness:05.13 kurtosis:025.86
v_8 skewness:00.20 kurtosis:-00.64
v_9 skewness:00.42 kurtosis:-00.32
v_10 skewness:00.03 kurtosis:-00.58
v_11 skewness:03.03 kurtosis:012.57
v_12 skewness:00.36 kurtosis:000.26
v_13 skewness:00.27 kurtosis:-00.44
v_14 skewness:-1.19 kurtosis:002.39
price skewness:03.31 kurtosis:018.40
绘制特征之间的关系图
# 数字特征相互之间关系的可视化
sns.set()
columns = ['price','v_12','v_8','v_0','power','v_5','v_2','v_6','v_1','v_14']
sns.pairplot(Train_data[columns],size=2,kind='scatter',diag_kind='kde')
plt.show()
绘制类别特征分布图，因为name和regionCode类别太稀疏了，因此这里没有画出稀疏的类。
# 类别特征箱型图可视化
categorical_features = ['model','brand','bodyType','fuelType','gearbox','notRepairedDamage']
for c in categorical_features:
Train_data[c] = Train_data[c].astype('category')
if Train_data[c].isnull().any():
Train_data[c] = Train_data[c].cat.add_categories(['MISSING'])
Train_data[c] = Train_data[c].fillna('MISSING')
def boxplot(x,y,**kwargs):
sns.boxplot(x=x,y=y)
x = plt.xticks(rotation=90)
f = pd.melt(Train_data,id_vars=['price'],value_vars=categorical_features)
g = sns.FacetGrid(f,col='variable',col_wrap=2,sharex=False,sharey=False,size=5)
g = g.map(boxplot,'value','price')
听课数据分析
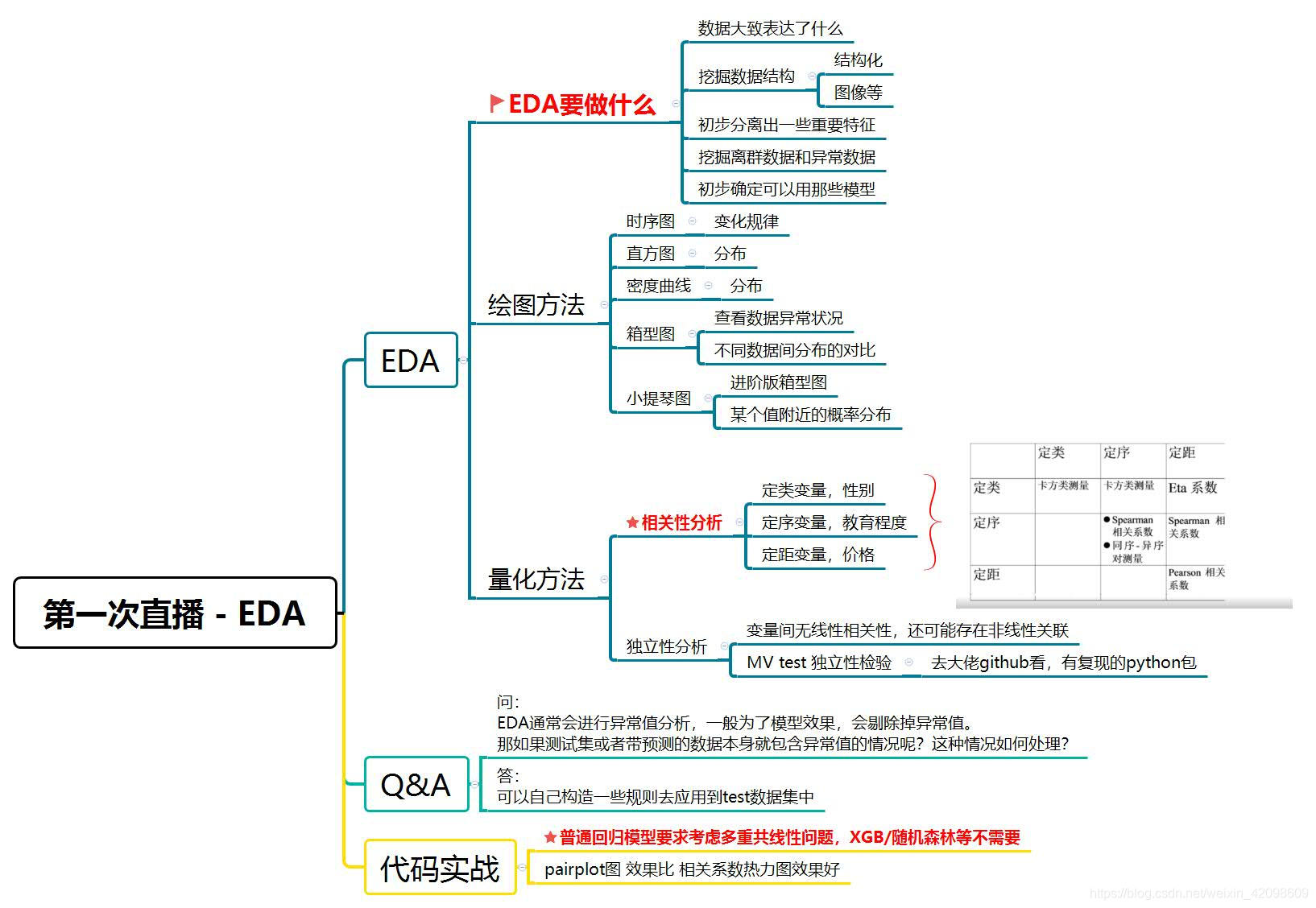
探索性数据分析（EDA）
（1）首先观察赛题、数据表达了什么
（2）探索数据的结构：图像、表格、时间序列
（3）锁定有效特征
（4）查找异常数据
（5）根据数据统计选择合适的模型
绘图方法
- 根据原始数据画图：时序图（折线）、直方图（便于观察数据分布）、密度曲线图、箱型图（便于查看数据的异常状况，以及不同数据间分布的对比）、小提琴图（箱型图进阶版，可以看出某个值附近分布的频率）
- 统计图：均值图、箱型图、残差图
量化方法
计算统计量、看看数据范围、看看数据分布
相关性分析方法
定类变量：名义型变量：如性别
定序变量：不仅分类，还按某种特性排序；两只的差无意义；如电影评分
定距变量：可比较大小、差有意义的变量
| Name | 定类 | 定序 | 定距 |
|---|---|---|---|
| 定类 | 卡方类检测 | 卡方类检测 | Eta系数 |
| 定序 | - | Spearman相关系数、同序-异序对测量 | Spearman相关系数 |
| 定距 | - | - | Pearson相关系数 |
独立性分析
变量间无线性相关性，还可能存在非线性关联。
听课没记全T-T，贴两张杨煜队伍的分享图，感谢大佬分享！
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
