一文带你看懂CNN反向传播原理

最新推荐文章于 2025-07-07 14:33:57 发布
原创 最新推荐文章于 2025-07-07 14:33:57 发布 · 3.5k 阅读 · 24 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#cnn

本文详细介绍了CNN模型中反向传播的过程，从全连接层、激活层到损失函数的计算，通过链式法则求解权重梯度，并使用梯度下降法更新权重。讲解了误差的定义及其在网络训练中的作用，帮助理解深度学习中参数优化的原理。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

看这篇文章，看官需要了解常规CNN模型的结构，并且了解结构下的各层计算逻辑。

OK，我们这次对CNN从全连接层到计算损失函数大致三个阶段进行推导和分析。

 

全连接层——激活层（一般只把它看做一个函数，但是其实keras里面把它作为一个层）——输出层（计算损失）

 

1、假设全连接层的输入（即上一层的输出）为x，全连接层的权重参数（神经元）为w，则全连接层的输出为

这个过程是一个矩阵的乘法运算。那为了计算的方便，我们就以两个变量举例，则全连接层输出为：

 

2、激活层的激活函数我们用relu，然后对于X的负轴方向我们不需要考虑，因为都是0嘛，那怎么计算都是0。假设正轴部分是y=kx，即斜率为k的x轴正向直线部分。于是

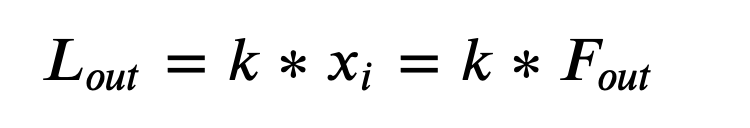
这里的x就是上一层的输出，即F

 

3、损失函数我们选用平方损失函数，写起来简单一些，并且假设只有一个输出。

最低0.47元/天 解锁文章

200万优质内容无限畅学
一文弄懂神经网络中的反向传播法——Back Propagation
迈微AI研习社 · 号主
10-08 759
点击上方“迈微电子研发社”，选择“星标★”公众号重磅干货，第一时间送达最近在看深度学习的东西，一开始看的吴恩达的UFLDL教程，有中文版就直接看了（点击这里文章第三部分观看）；后来发现有...
什么是GoogLeNet？一文看懂CNN经典模型GoogLeNet 从Inception v1到v4的演进
Marcus-Bao的个人主页
05-06 732
上一次我们谈到了CNN经典模型VGGNet，今天我们来简单聊聊比VGG更强大的GoogLeNet。 为什么有GoogLeNet? 2014年，GoogLeNet和VGG是当年ImageNet挑战赛(ILSVRC14)的双雄，GoogLeNet获得了第一名、VGG获得了第二名，这两类模型结构的共同特点是层次更深了。VGG继承了LeNet以及AlexNet的一些框架结构，而GoogLeNet则做了...
干货 | 深度学习之CNN反向传播算法详解
机器学习算法与Python学习
11-22 7148
微信公众号 关键字全网搜索最新排名 【机器学习算法】：排名第一 【机器学习】：排名第一 【Python】：排名第三 【算法】：排名第四 前言 在卷积神经网络(CNN)前向传播算法（干货 | 深度学习之卷积神经网络（CNN）的前向传播算法详解）中对CNN的前向传播算法做了总结，基于CNN前向传播算法的基础，下面就对CNN的反向传播算法做一个总结。在阅读本文前，建议先研究DNN的反向
CNN详解——反向传播过程
lengyue815的博客
11-03 2088
每一个输出特征图可能是多个输入特征图的组合的卷积结果。w(l)ij w i j ( l ) 的变化只会影响到下一层的第 i 个节点的输入值，且变化值会被放大 a(l)j a j ( l ) 倍，因此为 δ(l+1)ia(l)j δ i ( l + 1 ) a j ( l )。（1） klij(uv) k i j ( u v ) l 为第 l−1 l − 1 层到第 l l 层的第 j j 个卷积核中与第 l−1 l − 1 层第 i i 个通道相连接的卷积层上的第 u u 行第 v v 列的值。
【AI大模型】神经网络反向传播：核心原理与完整实现
woaiyitiaochaiya的博客
07-07 962
反向传播是神经网络训练的核心算法，通过链式法则高效计算梯度，解决了参数规模爆炸带来的计算瓶颈。文章详细解析了反向传播的数学原理（链式法则、关键梯度计算），对比了前向/反向传播的计算复杂度，并提供了Python实现代码（含可视化）。同时介绍了激活函数导数、优化技巧（梯度检查、裁剪）、常见问题解决方案（梯度消失/爆炸、局部最优）及现代优化器（SGD、Adam）中的应用。工程实现要点包括向量化计算和GPU加速等，为理解神经网络训练机制提供了全面指导。
CNN反向传播
Swift's Blog
06-08 498
深度神经网络(DNN)反向传播的公式推导可以参考之前的博客：https://transformerswsz.github.io/2019/05/29/反向传播/。 要套用DNN的反向传播算法到CNN，有几个问题需要解决： 池化层没有激活函数，我们可以令池化层的激活函数为 g(z)=zg(z) = zg(z)=z，即激活后输出本身，激活函数的导数为1。 池化层在前向传播的时候，对输入矩阵进行了压缩...
CNN的反向传播
qq_45870250的博客
11-13 1886
理解CNN(神经网络）怎么进行反向传播，怎么更新到上一层的参数，每一层参数更新的过程
一文带你看懂深度学习中完整的模型训练流程
最新发布
07-28
一文带你看懂深度学习中完整的模型训练流程，为我们揭示了如何从零开始构建一个深度学习模型，并通过实践来理解模型训练的各个环节。 首先，模型构建是深度学习的基础，涉及到选择合适的网络架构，如卷积神经网络...
一文看懂25个神经网络模型.pdf
05-13
这篇文档《一文看懂25个神经网络模型》旨在帮助读者理清当前流行的多种神经网络架构。本文将深入探讨几个关键的神经网络组件，包括神经元、卷积神经元、解卷积神经元、池化神经元和插值神经元，以及均值神经元和标准...
CNN的反向传播推导与理解
xunan003的博客
04-29 3056
参考与说明 本文主要是通过阅读相关论文和一些辅助的博文来理解卷积神经网络里面的反向传播算法；相关的论文可以查看Notes on Convolutional Neural Networks, Jake Bouvrie 准备工作 首先呢，我们还是先回顾下在深度学习里面的反向传播算法的公式，损失函数为 C=12∥y−aL∥2=12∑j(yj−aLj)2 公式如下    关于
卷积神经网络CNN的反向传播原理
Sual
08-07 3万+
　　上一篇博客《详解神经网络的前向传播和反向传播》推导了普通神经网络（多层感知器）的反向传播过程，这篇博客则讨论一下卷积神经网络中反向传播的不同之处。先简单回顾一下普通神经网络中反向传播的四个核心公式：...
DNN和CNN的反向传播算法（全连接层、卷积层、池化层）
qq_36665989的博客
08-20 1338
   反向传播算法是用来计算神经网络（NN）的可训练参数的偏导数的算法。在神经网络的训练中，对于一个参数（例如权重）的更新，往往采用下面的式子。 wi,j=wi,j−α∑k∈B∂Jk∂wi,j. w_{i,j}=w_{i,j}-\alpha \sum_{k\in B}\frac{\partial J_k}{\partial w_{i,j}}. wi,j​=wi,j​−αk∈B∑​∂wi,j​∂Jk​​. 其中wi,jw_{i,j}wi,j​是某个我们想要更新的权重，α\alphaα是学习率（一般比较小，例如
CNN的反向传播推导
czp_374的博客
01-21 3038
卷积神经网络三个重要概念： 局部感受野（local receptive fields） 共享权重（shared weights） 池化（pooling） （1）局部感受野：在全连接的网络中，输入被描绘成纵向排列的神经元，但是在卷积网络中我们把它看成28x28的方形： 输入神经元的一小片区域会被连接到下一层隐层，这个区域被称为局部感受野，然后在输入图像中移动局部感受野，每移动一次，对应一个隐层...
【Stanford CNN课程笔记】4. 反向传播算法
elaine_bao的专栏
02-15 6195
本课程笔记是基于今年斯坦福大学Feifei Li, Andrej Karpathy & Justin Johnson联合开设的Convolutional Neural Networks for Visual Recognition课程的学习笔记。目前课程还在更新中，此学习笔记也会尽量根据课程的进度来更新。在这一章中，我们将介绍backpropagation,也就是反向传播算法。
CNN-损失函数、向前传播与反向传播
erfan_lang的博客
09-10 502
损失函数
CNN是如何进行全连接
weixin_44932631的博客
05-09 2798
最后的两列小圆球就是两个全连接层，在最后一层卷积结束后，进行了最后一次池化，输出了20个12*12的图像，然后通过了一个全连接层变成了1*100的向量。而最后一层的全连接层通过对前一层的全连接层进行1*1的卷积得到 全连接具体计算：其实就是有20*100个12*12的卷积核卷积出来的，对于输入的每一张图，用了一个和图像一样大小的核卷积，这样整幅图就变成了一个数了，如果厚度是20就是那20个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。 全连接的目的是什么呢？ 因为传统的网络我们的输出..
对于全连接层的理解 全连接层的推导
GoodShot的专栏
02-16 1万+
全连接层的推导全连接层的每一个结点都与上一层的所有结点相连，用来把前边提取到的特征综合起来。由于其全相连的特性，一般全连接层的参数也是最多的。全连接层的前向计算下图中连线最密集的2个地方就是全连接层，这很明显的可以看出全连接层的参数的确很多。在前向计算过程，也就是一个线性的加权求和的过程，全连接层的每一个输出都可以看成前一层的每一个结点乘以一个权重系数W，最后加上一个偏置值b得到，即 。如下图中第...
一文让你彻底了解卷积神经网络
热门推荐
比比的博客
08-03 21万+
卷积神经网络（Convolutional Neural Network，CNN）是一种前馈神经网络，它的人工神经元可以响应一部分覆盖范围内的周围单元，对于大型图像处理有出色表现。 它包括卷积层(convolutional layer)和池化层(pooling layer)。 对比：卷积神经网络、全连接神经网络 左图：全连接神经网络（平面），组成：输入层、激活函数、全连接层 右图：卷积神经...
一文彻底搞懂深度学习 - 反向传播
07-23
反向传播算法（Back-Propagation Algorithm，简称BP算法）是深度学习模型中用于优化神经网络参数的关键技术之一。其核心思想是通过链式求导法则，从输出层向输入层反向逐层计算神经网络中各参数的梯度，并利用这些梯度进行参数更新，从而最小化损失函数。 ### 神经网络与损失函数 在深度学习中，神经网络通过多层非线性变换将输入数据映射到输出空间。每层网络的参数（如权重和偏置）决定了模型的表达能力。为了衡量模型输出与真实标签之间的差异，通常定义一个损失函数（Loss Function），如均方误差（Mean Squared Error, MSE）或交叉熵损失（Cross-Entropy Loss）。反向传播的目标是通过最小化该损失函数来优化网络参数。 ### 反向传播的基本流程 反向传播算法的实现依赖于计算图（Computation Graph）的构建。在前向传播阶段，输入数据依次经过各层网络计算，最终得到输出结果。此时，损失函数的值也被计算出来。在反向传播阶段，系统利用链式法则从输出端开始，逐层计算损失函数对每个参数的偏导数，即梯度。这些梯度随后被用于参数更新，通常采用梯度下降法（Gradient Descent）或其变体（如Adam、RMSProp等）： $$ w_{\text{new}} = w_{\text{old}} - \eta \cdot \frac{\partial L}{\partial w} $$ 其中，$ w $ 是参数，$ L $ 是损失函数，$ \eta $ 是学习率。 ### 链式法则与梯度传播 反向传播的核心在于链式法则的应用。假设某一层的输出为 $ y = f(x) $，而损失函数 $ L $ 是 $ y $ 的函数，则损失函数对 $ x $ 的导数可以通过链式法则计算： $$ \frac{dL}{dx} = \frac{dL}{dy} \cdot \frac{dy}{dx} $$ 这一过程从输出层开始，逐层向前传播，确保每一层的参数都能根据其对最终损失的影响进行更新。这种从后向前的梯度传播机制使得神经网络能够高效地进行参数优化。 ### 自动微分与现代深度学习框架 现代深度学习框架（如TensorFlow、PyTorch）实现了自动微分（Automatic Differentiation），可以自动构建计算图并跟踪所有操作，使得用户只需定义前向传播过程，框架会自动处理反向传播的梯度计算。这种方式极大地简化了神经网络的实现过程，提升了开发效率[^2]。 以下是一个简单的PyTorch代码示例，展示了如何使用自动微分进行反向传播： ```python import torch # 定义可学习参数 w = torch.tensor([1.0], requires_grad=True) b = torch.tensor([0.5], requires_grad=True) # 前向传播 x = torch.tensor([2.0]) y_pred = w * x + b y_true = torch.tensor([3.0]) # 计算损失 loss = (y_pred - y_true) ** 2 # 反向传播 loss.backward() # 打印梯度 print("w的梯度:", w.grad) print("b的梯度:", b.grad) ``` ### 梯度更新与优化 在获得梯度后，模型通过优化器（如SGD、Adam等）对参数进行更新。以随机梯度下降（SGD）为例，其更新规则为： $$ w_{t+1} = w_t - \eta \cdot g_t $$ 其中，$ g_t $ 是当前批次的梯度估计值。Adam优化器在此基础上引入动量和自适应学习率机制，能够更有效地处理非凸优化问题。 ### 总结 反向传播算法通过链式法则高效地计算神经网络中各参数的梯度，是深度学习模型训练的核心机制。现代框架通过自动微分技术简化了其实现，使得开发者能够专注于模型设计与调优。反向传播不仅在理论层面具有坚实的数学基础，也在实际应用中展现出强大的优化能力。
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值