算法导论学习—— 22章 基本的图算法

图的表示

1. 邻接表表示方法：经常用于表示稀疏图(边数远小于节点数平方）
2. 邻接矩阵表示方法：可以用于表示稠密图（边数接近节点数平方）

广度优先搜索

采用队列操作，不断取出队首节点，搜索队首节点所邻未访问过的节点入队。记录搜索前驱可得到广度优先树，包含源节点到任意节点的最短路径。

深度优先搜索

采用栈操作，将栈顶节点所连未访问的节点压入栈顶，栈顶回到该节点时将其弹出。

拓扑排序

先统计每个节点入度，选择入度为零的点加入队列。每次选择队首节点，寻找出边相连节点，入度减一，新增入度为零的节点加入队列。重复操作直到队列为空。

强连通分量

考虑带时间标签的深度优先搜索，对于节点$v_i$，属性$v_i.d$表示$v_i$被发现时的时间标签，$v_i.f$表示$v_i$结束后续搜索回溯时的时间标签。对于两个连通分量$C,C^{\prime }$，有边$(u,v)$，其中$u\in C$，$v\in C^{\prime }$，则不存在边$(v,u)$，否则两个连通分量可以合并。而且$u.f>v.f$。证明如下：

1. 假设$u.d<v.d$，即搜索时先搜到$u$，则$v$在$u$的搜索子树中，$v$的全部搜索子树回溯时，$v$回溯。因此$u.f>v.f$。
2. 假设$u.d>v.d$，即搜索时先搜到$v$，则$u$无法由$v$搜索得到，即$u$不在$v$的搜索路径上。在$v$搜索结束后$u$才能被搜索到，因此$u.f>v.f$。

如下图所示，对该图深度优先搜索得到每个点的发现时间和结束时间。

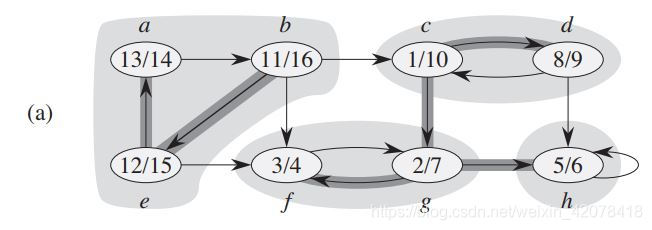
对于该图的转置，如下图

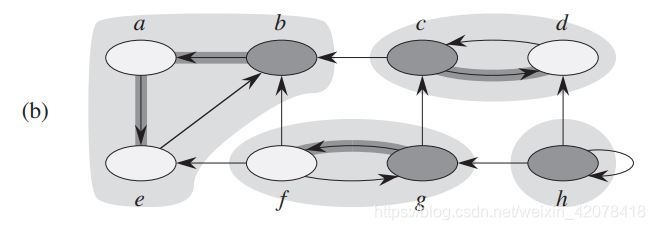
由上文证明可知，在转置图中，连接两个强连通分量的边都是从结束时间早的指向结束时间晚的。因此将原图的节点按照结束时间从大到小排序，进行深度优先搜索，获得不同的搜索子树即为不同的强连通分量。

代码实现

对于上文所示图像，进行代码实现如下

Strongly Connected Graph