支持向量机是一种分类算法,支持向量机可以分为:线性可分支持向量机、线性支持向量机和非线性支持向量机。
在介绍算法之前,先介绍支持向量机的基础超平面与划分超平面
1 超平面与划分超平面
超平面是n维欧氏空间中余维度等于一的线性子空间,也就是必须是(n-1)维度。这是平面中的直线、空间中的平面之推广(n大于3才被称为“超”平面),是纯粹的数学概念,不是现实的物理概念。因为是子空间,所以超平面一定经过原点。
上面的是百度百科中关于超平面的定义,超平面正确的数学表达式应该为 ω T x = 0 \omega^T x=0 ωTx=0,其中 ω 与 x \omega与x ω与x都是n维列向量, x x x表示超平面上的点, ω \omega ω表示超平面的法向量,决定了超平面的方向。看到不少博客中将超平面的数学形式写为 ω T x + b = 0 \omega^T x+b=0 ωTx+b=0,这显然是不对的,其实这个表达式表示的是支持向量机里的一个划分超平面(又称为仿射超平面),表达式中的 b b b表示超平面与原点的距离。
为了方便直观理解,以三维空间为例。假设 x , y , z x,y,z x,y,z分别表示三维空间里的三个维度,那么三维空间里的一个划分超平面可以表示为 w 1 x + w 2 y + w 3 z + b = 0 w_1 x +w_2 y+w_3 z + b =0 w1x+w2y+w3z+b=0,这是一个维度为2的平面。当 b = 0 b=0 b=0,这表示一个超平面,且这个超平面显然是经过原点的。(想画个图表示的,手艺太差,自行想象吧 ?,这里有三种特殊情况, x , y , z x,y,z x,y,z分别等于0时也是超平面)。
支持向量机里的划分超平面可以将其所在的空间分为两个半空间,划分超平面法向量所指向的那一面称为正面(即 ω T x + b > 0 \omega^T x+b>0 ωTx+b>0),另外一面称为反面即 ω T x + b < 0 \omega^T x+b<0 ωTx+b<0)。可以用这个性质进行分类,通过验证 ω T x + b \omega^T x+b ωTx+b与样本标签 y y y是否同号来判断分类正确与否。
为了便于表示,将划分超平面
ω
T
x
+
b
\omega^T x +b
ωTx+b称为超平面
(
ω
,
b
)
(\omega,b)
(ω,b)。定义函数间隔
γ
′
=
y
(
ω
T
x
+
b
)
\gamma'=y(\omega^T x+b)
γ′=y(ωTx+b),函数间隔可以反应对样本点的分类正确与否,但并不能正常反应点到超平面的距离。样本空间中任意一点
x
x
x到超平面
(
w
,
b
)
(w,b)
(w,b)的几何距离可以表示为:
r
=
∣
w
T
x
+
b
∣
∣
∣
w
∣
∣
,
r=\frac{|w^Tx+b|}{||w||},
r=∣∣w∣∣∣wTx+b∣,
几何距离可以反应点到超平面的距离,但并不能反应分类的正确与否。可以将函数间隔与几何距离相统一,并定义几何间隔
γ
=
y
(
w
T
x
+
b
)
∣
∣
w
∣
∣
=
γ
′
∣
∣
w
∣
∣
,
\gamma=\frac{y(w^Tx+b)}{||w||}=\frac{\gamma'}{||w||},
γ=∣∣w∣∣y(wTx+b)=∣∣w∣∣γ′,
显然,几何间隔不仅能反应点到超平面的距离,还可以反应模型对样本点的分类正确与否。
2 线性可分支持向量机
我们可以直接使用上一节中得到的几何间隔作为目标函数,使几何间隔最大,即:
max
y
(
w
T
x
+
b
)
∣
∣
w
∣
∣
\textrm{max}\quad\frac{y(w^Tx+b)}{||w||}
max∣∣w∣∣y(wTx+b)
如果有两类样本点分布如下图所示,几何间隔表示两类样本点与分离超平面的距离,称两类样本点中离划分超平面最近的样本点为“支持向量”(support vector), 并且我们令支持向量到划分超平面的函数间隔为1,即
y
(
ω
T
x
+
b
)
≥
1
y(\omega^T x+b)\geq1
y(ωTx+b)≥1。
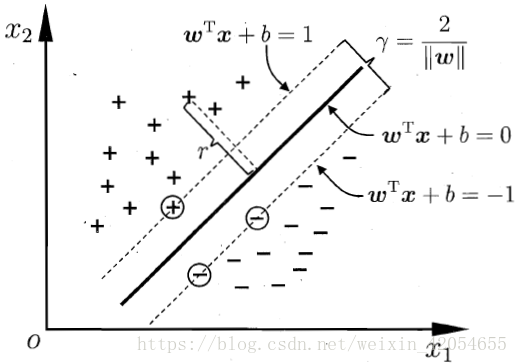
那么,上面的式子可以转化为:

显然,最大化
∣
∣
w
−
1
∣
∣
||w^{-1}||
∣∣w−1∣∣,等价于最小化
∣
∣
w
2
∣
∣
||w^2||
∣∣w2∣∣。所以,SVM的优化函数也等价于:

上面的目标函数为凸函数,约束条件是仿射的,该问题是一个凸二次规划问题,可以运用拉格朗日函数将上述问题转化为无约束的优化函数,添加拉格朗日乘子
α
i
≥
0
\alpha_i \geq 0
αi≥0, 此时该问题的优化函数转化为:
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
L(w,b,\alpha)=\frac{1}{2}||w||^2 + \sum_{i=1}^{m}\alpha_i(1-y_i(w^Tx_i+b))
L(w,b,α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))
令
L
(
w
,
b
,
α
)
L(w,b,\alpha)
L(w,b,α)对
w
w
w和
b
b
b的偏导为0,可得:
w
=
∑
i
=
1
m
α
i
y
i
x
i
;
0
=
∑
i
=
1
m
α
i
y
i
w=\sum_{i=1}^m\alpha_iy_ix_i;0=\sum_{i=1}^m\alpha_iy_i
w=∑i=1mαiyixi;0=∑i=1mαiyi;这样就求得了
w
w
w与
α
\alpha
α的函数关系,并将其代回
L
(
w
,
b
,
α
)
L(w,b,\alpha)
L(w,b,α)中,可以消去
w
w
w。
令
φ
(
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
)
\varphi(\alpha)=\frac{1}{2}||w||^2+\sum_{i=1}^m\alpha_i(1-y_i(w^Tx_i+b))
φ(α)=21∣∣w∣∣2+i=1∑mαi(1−yi(wTxi+b))
根据L2范式的性质:
∣
∣
w
∣
∣
2
2
=
w
T
w
||w||_2^2=w^T w
∣∣w∣∣22=wTw,及
w
=
∑
i
=
1
m
α
i
y
i
x
i
w=\sum_{i=1}^m\alpha_iy_ix_i
w=∑i=1mαiyixi,上式可以化为:
φ
(
α
)
=
1
2
(
∑
i
=
1
m
α
i
y
i
x
i
)
T
∑
i
=
1
m
α
i
y
i
x
i
+
∑
i
=
1
m
α
i
−
(
∑
i
=
1
m
α
i
y
i
x
i
)
T
∑
i
=
1
m
α
i
y
i
x
i
−
b
∑
i
=
1
m
α
i
y
i
\varphi(\alpha)=\frac{1}{2}(\sum_{i=1}^m\alpha_iy_ix_i)^T\sum_{i=1}^m\alpha_iy_ix_i+\sum_{i=1}^m\alpha_i-(\sum_{i=1}^m\alpha_iy_ix_i)^T\sum_{i=1}^m\alpha_iy_ix_i-b\sum_{i=1}^m\alpha_i y_i
φ(α)=21(i=1∑mαiyixi)Ti=1∑mαiyixi+i=1∑mαi−(i=1∑mαiyixi)Ti=1∑mαiyixi−bi=1∑mαiyi
φ
(
α
)
=
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
α
i
y
i
x
i
T
∑
i
=
1
m
α
i
y
i
x
i
−
b
∑
i
=
1
m
α
i
y
i
\varphi(\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\alpha_iy_ix_i^T\sum_{i=1}^m\alpha_iy_ix_i-b\sum_{i=1}^m\alpha_i y_i
φ(α)=i=1∑mαi−21i=1∑mαiyixiTi=1∑mαiyixi−bi=1∑mαiyi
又由于
0
=
∑
i
=
1
m
α
i
y
i
0=\sum_{i=1}^m\alpha_iy_i
0=∑i=1mαiyi,所以:
φ
(
α
)
=
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
m
α
i
y
i
x
i
T
∑
i
=
1
m
α
i
y
i
x
i
\varphi(\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\alpha_iy_ix_i^T\sum_{i=1}^m\alpha_iy_ix_i
φ(α)=i=1∑mαi−21i=1∑mαiyixiTi=1∑mαiyixi
φ
(
α
)
=
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
,
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
\varphi(\alpha)=\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1,j=1}^m\alpha_i \alpha_j y_i y_j x_i^T x_j
φ(α)=i=1∑mαi−21i=1,j=1∑mαiαjyiyjxiTxj
对
φ
(
α
)
\varphi(\alpha)
φ(α)求极大化的数学形式可以表达为:
max
∑
i
=
1
m
α
i
−
1
2
∑
i
=
1
,
j
=
1
m
α
i
α
j
y
i
y
j
x
i
T
x
j
\max \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1,j=1}^m\alpha_i \alpha_j y_i y_j x_i^T x_j
maxi=1∑mαi−21i=1,j=1∑mαiαjyiyjxiTxj
s.t.
∑
i
=
1
m
=
0
i
=
1
,
2
,
.
.
.
m
\textrm{s.t.}\sum_{i=1}^m=0\quad i=1,2,...m
s.t.i=1∑m=0i=1,2,...m
α
i
≥
0
,
i
=
1
,
2
,
.
.
.
m
\alpha_i\geq0,i=1,2,...m
αi≥0,i=1,2,...m
该问题是SVM问题的对偶问题,通过求出对应的
α
\alpha
α,进而可以求出
w
和
b
w和b
w和b,就可得到最终的分类决策函数:
f
(
x
)
=
s
i
g
n
(
∑
i
=
1
m
α
i
y
i
x
i
T
x
i
+
b
)
f(x)=sign(\sum_{i=1}^m\alpha_iy_ix_i^Tx_i +b)
f(x)=sign(i=1∑mαiyixiTxi+b)
具体求解
α
\alpha
α,通常使用的是SMO算法,该算法知识参加西瓜书。
由于原函数是凸函数,满足KKT条件,具体为:

每一个
α
i
\alpha_i
αi对应着训练样本
(
x
i
,
y
i
)
(x_i,y_i)
(xi,yi),总有
α
i
=
0
或
y
i
f
(
x
i
)
=
1
\alpha_i=0或y_if(x_i)=1
αi=0或yif(xi)=1
我们可以推出支持向量机的一个重要性质:机器学习最终模型仅与支持向量有关。








 本文介绍了支持向量机的基础概念,包括超平面与划分超平面,强调了超平面的数学表达式以及其在分类中的作用。重点讲述了线性可分支持向量机,目标是最大化几何间隔,通过拉格朗日乘子法转换为无约束优化问题,最后提出了对偶问题并简要提及SMO算法。支持向量机的关键在于,最终模型仅与支持向量相关。
本文介绍了支持向量机的基础概念,包括超平面与划分超平面,强调了超平面的数学表达式以及其在分类中的作用。重点讲述了线性可分支持向量机,目标是最大化几何间隔,通过拉格朗日乘子法转换为无约束优化问题,最后提出了对偶问题并简要提及SMO算法。支持向量机的关键在于,最终模型仅与支持向量相关。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








