洛谷3225 矿场搭建

洛谷3225 矿场搭建

题目链接： 洛谷3225 矿场搭建

题意： 给了N( N<=50 )条边，让你建立逃生点，要求图中任意一个点爆炸都能保证其他点的工人能逃生，求最少要建立多少个逃生点，并求建立逃生点的方案总数。

思路： 这题很明显和求割点有关，一旦割点被炸毁连通块(注意这里并不一定是点双连通分量v-DDC，很多题解这里概念都搞错了，弄得我前期读题解读的一愣一愣的)数目都会增加，即各个点之间的连通性都会发生改变。关键是求出割点后的后续讨论。这里肯定要将割点所连接的各个连通块拆开来讨论，因为合在一起，需要考虑割点是否被炸毁后还要考虑割点所连接的各个连通块中是否还需要设立逃生点，讨论起来会变得非常复杂。下面讨论拆分开的各个连通块内部的情况（以下图解中的图片均来自洛谷）。

情况一： 分割连通块后，该连通块中无原图的割点。此时的连通块就满足
v-DCC，即无论去掉连通块中哪一个点都不影响连通性。本应只用任选一处作逃生点，但考虑到刚好设置的一处逃生点坍塌的情况我们至少需要任意设置两个逃生点。方案数C(n, 2)

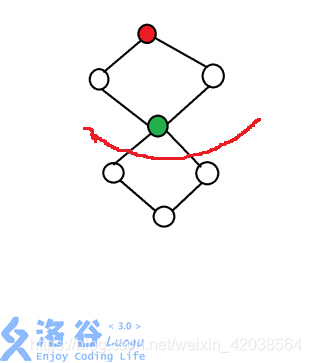
情况二： 连通块中只有一个原图的割点。如下图所示上下两个连通块共享一个割点，此时讨论的是割点被划入上半部分，上半部分只有一个割点。我们只需要在这一连通块的非割点建一个逃生点即可，若是该逃生点被炸毁，我们可以通过绿色割点逃到别的连通块( 这里默认别的连通块可逃生，因为不可能以割点进行连通块切割后所有的连通块都有两个及以上割点不设立逃生点，那是情况三)逃生；若是割点被炸毁，我们可以通过逃生点逃生。这个连通块的可选方案数应该是 n-1 个，这里dfs中对结点计数不要计割点就好。

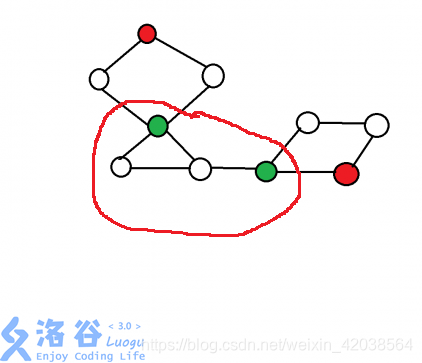
情况三： 连通块中有两个及以上原图的割点。如下图红圈所示连通块，此时后期找连通块 dfs 时是由红圈内部某个非割点结点开始，遍历到边界两个割点出停止，造成了一个连通块内含两个(及以上)割点的情况。此时该连通块无需设立逃生点：若炸毁其中一个割点，则可以由另一个割点逃至别的连通块进行逃生；若炸毁的不是割点，则每个点可以选取本连通块内与自己相通的割点逃到别的连通块进行逃生，因而也不需要统计方案数。

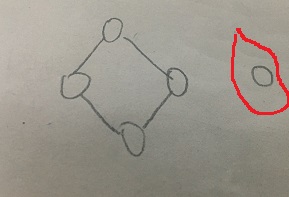
情况四： 这种属于连通块中只有一个结点的特殊情况。洛谷没找到图，手绘版不要嫌弃。

(1). 在原图中本身与其他结点不相连。这时还是需要在这一点设置逃生点，要是被炸毁了当然不用逃了，要是没有被炸毁，这一结点的人还是要逃的。逃生点总数+1，方案总数1不变。

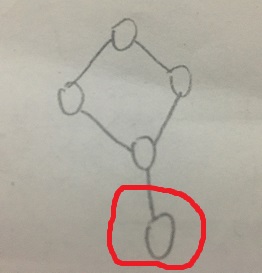
(2). 原图中该节点与割点相连，后面 dfs 切割连通块时被单独隔离出来。此时还是要在该点设立逃生点，因为其所连的割点一旦被炸毁还是要靠本结点自己逃生。逃生点总数+1，方案总数1不变。

综上所有的情况就都齐全了，后面Tarjan处理出割点后，以非割点为起点，以割点为阻隔点，跑连通块统计连通块内部结点数目及割点数目分类计算即可。

代码实现：

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define mem( f, x ) memset( f, x, sizeof( f ) )
#define INF 0x3f3f3f3f
#define pii pair<int, int>
#define mk( x, y ) make_pair
#define fi first
#define se second
#define pk push_back
using namespace std;
const int N = 20005;
const int M = 505;
int m, n;
int head[N], cnt;
int dfn[N], low[N], ck_num, root;
bool cut[N];
int color[N], col_num;
int cut_num, node_num;

struct eg{
    int to, pre;
    eg( ){ to = pre = 0; }
    eg( int tt, int pp ){
        to = tt, pre = pp;
    }
}e[2*M];

void add( int x, int y ){
    e[++cnt] = eg( y, head[x] );
    head[x] = cnt;
}


void init( ){
    mem( head, 0 );
    mem( dfn, 0 );
    mem( low, 0 );
    mem( cut, 0 );
    mem( color, 0 );
    cnt = n = ck_num = col_num = 0;
}

//Tarjan 跑割点
void Tarjan( int cur ){
    dfn[cur] = low[cur] = ++ck_num;
    int ct = 0;
    for( int i = head[cur]; i; i = e[i].pre ){
        int to = e[i].to;
        if( !dfn[to] ){
            ct++;
            Tarjan(to);
            low[cur] = min( low[cur], low[to] );
            if( cur == root && ct > 1 ) cut[cur] = 1;
            if( cur != root && low[to] >= dfn[cur] ) cut[cur] = 1;
        }
        else
            low[cur] = min( low[cur], dfn[to] );
    }
}

//dfs 统计以割点为分割点的连通块中割点数目和割点外的结点数目
void dfs( int cur, int fa ){
    color[cur] = col_num;
    node_num++;
    for( int i = head[cur]; i; i = e[i].pre ){
        int to = e[i].to;
        if( color[to] != color[cur] ){ //同一连通块中结点不重复遍历
            color[to] = col_num;
            if( !cut[to] ) 
                dfs( to, cur );
            else //割点分界
                cut_num++;
        }
    }
}

int main( ){
    int ct = 1;
    while( scanf( "%d", &m ) != EOF && m ){
        int x, y;
        init( );
        while( m-- ){
            scanf( "%d %d", &x, &y );
            add( x, y );
            add( y, x );
            n = max( n, x );
            n = max( n, y );
        }
        for( int i = 1; i <= n; i++ ){
            if( !dfn[i] ){
                root = i;
                Tarjan( i );
            }
        }

        ull sum = 1, num = 0;
        for( int i = 1; i <= n; i++ ){
            if( !color[i] && !cut[i] ){
                cut_num = node_num = 0;
                col_num++;
                dfs( i, 0 );
                if( !cut_num ){ //0个割点
                    if( node_num > 1 ){
                        num += 2;
                        sum *= node_num*(node_num-1)/2;
                    }
                    else
                        num += 1;
                }
                else if( cut_num == 1 ){ //1个割点
                    num += 1;
                    sum *= node_num;
                }
                //2个及以上割点情况不用设立逃生点
            }
        }
        printf( "Case %d: %llu %llu\n", ct++, num, sum );
    }
    return 0;
}

在这里插入代码片