1. 什么是二叉树
一棵二叉树是有限个节点的集合,其中每个节点至多只有2个子节点。
二叉树可以是空树,可以只有一个根节点,可以是一个根节点加一个子节点组成的树。
2. 二叉树与普通树的区别
①子节点的限制:一般树对节点的子节点个数没有限制,而二叉树中每个节点至多只能有2个子节点。
②子节点的区分:一般树不对节点的子节点进行区分,而二叉树将节点的子节点分为左孩子(left)和右孩子(right)。
3. 特殊二叉树
3.1 完全二叉树
除最底层外,每层的节点个数都达到了最大数(根节点视为第1层,第n(n= 1, 2…)层的节点个数最大值为2^n),且最底层的节点是从左往右依次排列。

高度为 4 的完全二叉树
3.2 满二叉树
除最底层的节点(都是叶节点)外,每个节点都具有两个子节点。
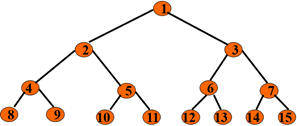
高度为 3 的满二叉树
满二叉树是特殊的完全二叉树。
4. 二叉树的性质
(1) 第n(n=1, 2…)层的节点最多有2^(n-1)个节点。
(2) 高度为k(k=1, 2…)的二叉树最多有2^k - 1个节点,最少有k个节点。
(3) 一棵二叉树,若其叶节点数为n(0),度为2的节点总数为n(2),则n(0) = n(2) + 1
(4) 具有n个节点的完全二叉树,其深度k为:k = log(2) n + 1
(5) 有n个节点的完全二叉树,各节点如果用顺序方式存储,对任意节点i,有如下关系:如果 i!=1,则其父节点的编号为 i/2;
如果2*i<=n,则其左子树根节点的编号为2*i;
如果2*i>n,则该节点无左子树;
如果2*i+1<=n,则其右子树根节点编号为2*i+1,;
如果2*i+1>n。则该节点无又子树。
5. 二叉树的存储
5.1 数组存储
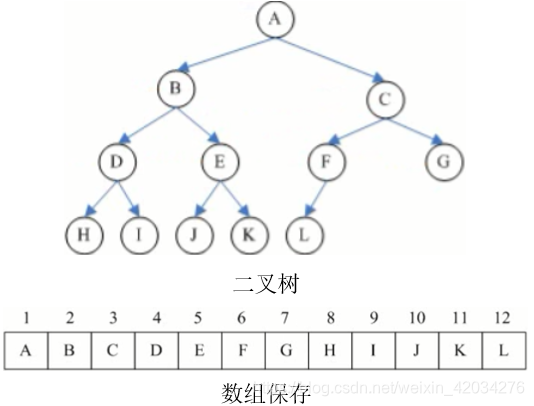
完全二叉树用这种方式保存很容易进行检索,无论是已知子节点找父节点,还是已知父节点找子节点,都很方便(利用上一节中的性质)。
如果不是完全二叉树,可以利用某些方法来将二叉树转换成完全二叉树,将缺少的节点设置为空。
5.2 链式存储
实际上,二叉树的每个节点之间没有绝对的位置关系,用链式存储会是更好的选择。链式存储通常有二叉链式存储和三叉链式存储两种存储方式。
二叉链式存储
每一个节点保存三个属性:自身数据、左孩子、右孩子。
|
left |
data |
right |
缺点:无法通过该节点找到其父节点,只适合不用经常回溯父节点的场景。
三叉链式存储
每个节点都保存四个内容:本身数据、左孩子、右孩子、父节点。
|
left |
data |
right |
parent |
缺点:内存开销大。





 本文介绍了二叉树的基本概念,包括它与普通树的区别,特别是完全二叉树和满二叉树的特性。接着,讨论了二叉树的性质,如层数、节点数量的关系。此外,还探讨了二叉树的两种存储方式:数组存储(适用于完全二叉树)和链式存储(包括二叉链式和三叉链式)。
本文介绍了二叉树的基本概念,包括它与普通树的区别,特别是完全二叉树和满二叉树的特性。接着,讨论了二叉树的性质,如层数、节点数量的关系。此外,还探讨了二叉树的两种存储方式:数组存储(适用于完全二叉树)和链式存储(包括二叉链式和三叉链式)。
















 710
710

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








