@SuppressWarnings("unchecked")
public class SegmentTree<E>{
private E[] data;
private E[] tree;
private Merger<E> merger;
public SegmentTree(E[] arr,Merger<E> merger) {
this.merger = merger;
data = (E[]) new Object[arr.length];
for(int i=0;i<arr.length;i++) {
data[i] = arr[i];
}
tree = (E[]) new Object[4*arr.length];
bulidSegmentTree(0,0,data.length-1);
}
//创建线段树
private void bulidSegmentTree(int treeIndex,int l,int r) {
if(l==r) {
tree[treeIndex] = data[l];
return;
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = l + (r-l)/2;
bulidSegmentTree(leftTreeIndex,l,mid);
bulidSegmentTree(rightTreeIndex,mid+1,r);
tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
}
private int leftChild(int index) {
return 2*index+1;
}
private int rightChild(int index) {
return 2*index+2;
}
//查询 返回区间[queryL,queryR]的值
public E query(int queryL,int queryR) {
if(queryL < 0 || queryL >=data.length || queryR <0 || queryR >= data.length || queryL > queryR ) {
throw new IllegalArgumentException("Index is illegal");
}
return query(0,0,data.length-1,queryL,queryR);
}
private E query(int treeIndex,int l,int r,int queryL,int queryR) {
if(l==queryL && r == queryR) {
return tree[treeIndex];
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = l + (r-l)/2;
//刚好落入左节点和右节点的情况
if(queryL >= mid+1) {
return query(rightTreeIndex,mid+1,r,queryL,queryR);
}else if(queryR <= mid) {
return query(leftTreeIndex,l,mid,queryL,queryR);
}
//[queryL,mid]
E leftResult = query(leftTreeIndex,l,mid,queryL,mid);
//[mid+1,queryR]
E rightResult = query(rightTreeIndex,mid+1,r,mid+1, queryR);
return merger.merge(leftResult,rightResult);
}
//更新
private void set(int index,E e) {
if(index < 0 || index>=data.length)
throw new IllegalArgumentException("Index is illegal");
data[index] = e;
set(0,0,data.length-1,index,e);
}
private void set(int treeIndex,int l,int r,int index,E e) {
if(l==r) {
tree[treeIndex] = e;
return;
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = l + (r-l)/2;
if(index >= mid+1)
set(rightTreeIndex,mid+1,r,index,e);
else
set(leftTreeIndex,l,mid,index,e);
tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
}
//测试
public void getSegmentTree() {
for(int i=0;i<tree.length;i++) {
System.out.println(tree[i]);
}
}
public static void main(String[] args) {
Integer[] nums = {1,2,3,4,5};
SegmentTree<Integer> seg = new SegmentTree<>(nums,new Merger<Integer>() {
public Integer merge(Integer a,Integer b) {
return a+b;
}
});
seg.getSegmentTree();
}
}






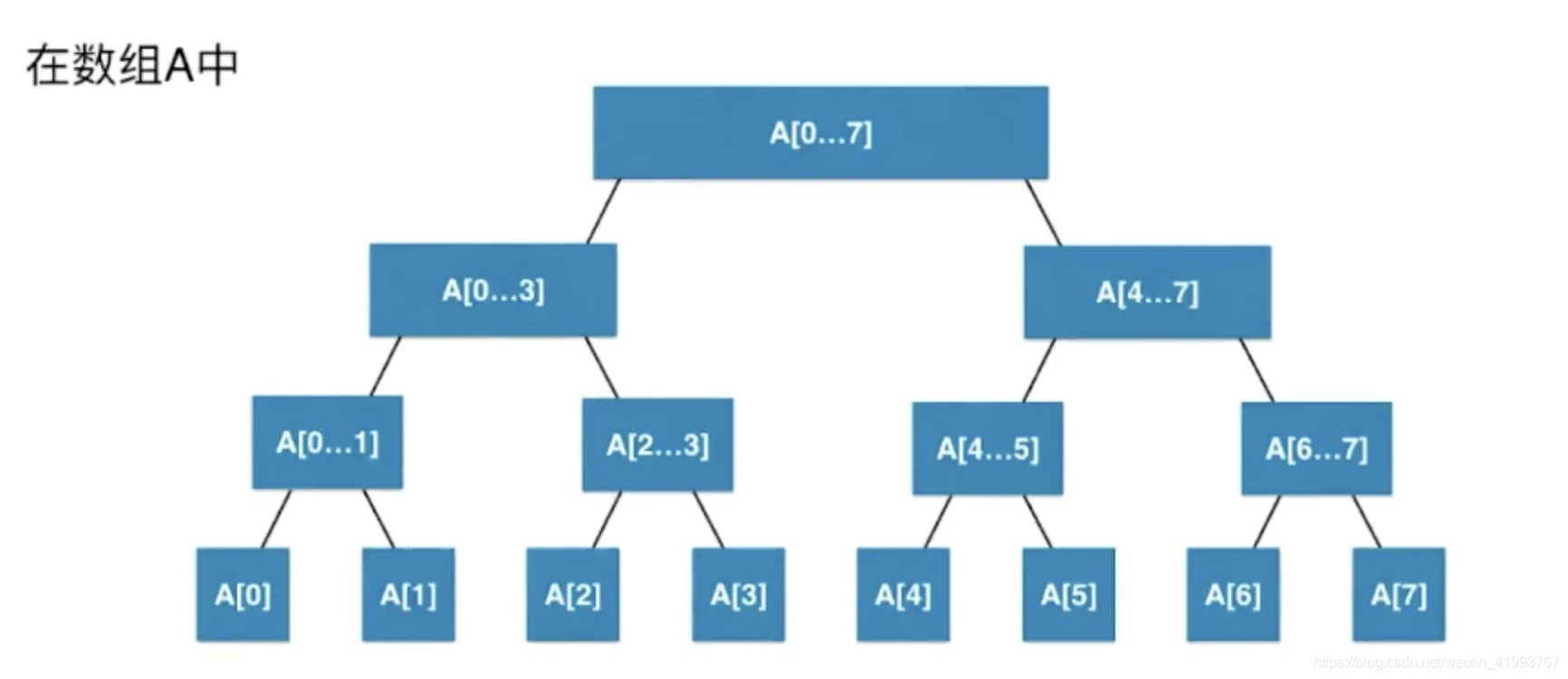
 本文深入探讨了段树数据结构的实现与应用,通过具体的Java代码示例,讲解了如何构建段树,进行区间查询及更新操作。段树是一种高效的数据结构,常用于解决区间查询和动态更新问题。
本文深入探讨了段树数据结构的实现与应用,通过具体的Java代码示例,讲解了如何构建段树,进行区间查询及更新操作。段树是一种高效的数据结构,常用于解决区间查询和动态更新问题。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








