机器学习基础--VC Dimension

主要参考：

http://www.mamicode.com/info-detail-1148920.html

https://blog.youkuaiyun.com/yc1203968305/article/details/78574174

https://blog.youkuaiyun.com/dQCFKyQDXYm3F8rB0/article/details/87484494

VC Dimension 作用：

VC Dimension 的作用为衡量假设集合的好坏。假设集合具体来说就为某种模型（线性，SVM）等。它衡量的是一模型在某一方面的性能，和模型的优劣无关。比如说逻辑回归它是一个模型，它就是一个假设集合。这个 VC Dimension 它衡量的就是逻辑回归在某一方面能力怎么样，或者是决策树在某一方面能力怎么样，它还没有到评估说具体某一个拟合出来的模型好不好。从VC Dimension 可以了解到：为什么某机器学习方法是可学习的？为什么会有过拟合？拿什么来衡量机器学习模型的复杂度？深度学习与VC Dimension 的关系？

VC Dimension 定义：
      1. Hoeffding不等式：关于一组随机变量均值的概率不等式。

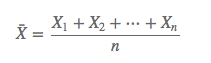为随机变量均值。                                                                                           为Hoeffding不等式。

衡量随着样本量n的增大，样本期望（x把）越来越接近总体期望E(x把)。

       2.机器学习与Hoeffding不等式的联系：

机器学习的流程：

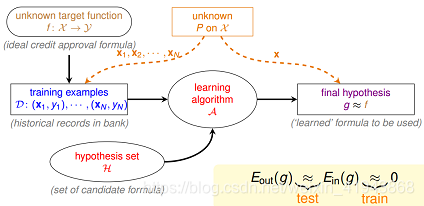
f 表示理想的方案(可以是一个函数，也可以是一个分布)，H 是该机器学习方法的假设空间，g 表示我们求解的用来预测的假设，g属于H。机器学习的过程就是：通过算法A，在假设空间H中，根据样本集D，选择最好的假设作为g。选择标准是 g 近似于 f。

拿perceptron来举例。

感知机（perceptron）是一个线性分类器(linear classifiers）。 线性分类器的几何表示：直线、平面、超平面。

perceptron的假设空间，用公式描述，如下所示：

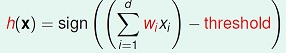
感知机的假设空间是定义在特征空间的所有线性分类模型或线性分类器。H={f|f(x)=sign(ω⋅x+b)}

感知器的优化目标如下式所示，w_g就是我们要求的最好的假设

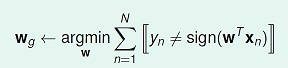
设定两个变量，如下图所示，图中 f(x)表示理想目标函数，h(x)是我们预估得到的某一个目标函数，h(xn)是假设空间H中的一个假设。

Eout(h)，可以理解为在理想情况下(已知f)，总体(out-of-sample)的损失(这里是0–1 loss)的期望，称作expected loss

Ein(h)，可以理解为在训练样本上(in-of-sample)，损失的期望，称作expirical loss

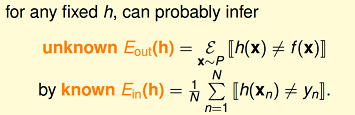
当训练样本量N足够大，且样本是独立同分布的.可以通过样本集上的expirical loss Ein(h) 推测总体的expected loss Eout(h)。基于hoeffding不等式，我们得到下面式子：

学习可行的两个核心条件

在往下继续推导前，先看一下什么情况下Learning是可行的？

1. 如果假设空间H的size M是有限的，当N足够大时，那么对假设空间中任意一个g，Eout(g)约等于Ein(g)；
2. 利用算法A从假设空间H中，挑选出一个g，使得Ein(g)接近于0，那么probably approximately correct而言，Eout(g)也接近为0；

上面这两个核心条件，也正好对应着test和train这两个过程。train过程希望损失期望(即Ein(g) )尽可能小；test过程希望在真实环境中的损失期望也尽可能小，即Ein(g)接近于Eout(g)。

在我们的假设空间H中，往往有很多个假设函数(甚至于无穷多个)，这里我们先假定H中有M个假设函数。

太多了。头疼！！！！！

下面我们以二维假设空间为例，来解释一下该空间下各假设在确定的训练样本上的重叠性。

举例来说，如果我们的算法要在平面上(二维空间)挑选一条直线方程作为g，用来划分一个点x1。假设空间H是所有的直线，它的size M是无限多的。但是实际上可以将这些直线分为两类，一类是把x1判断为正例的，另一类是把x1判断为负例的。如下图所示：

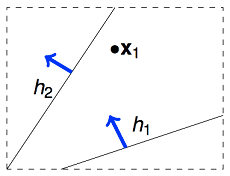
那如果在平面上有两个数据点x1,x2，这样的话，假设空间H中的无数条直线可以分为4类.第一类为把两条直线分为正类，第二类为把两条直线分为负类。第三类为把x1分为正类，x2分为负类。第四类为把x1分为负类，x2分为正类。

Effective Number of Hypotheses

对于这个有效的假设函数值，我们尝试用一个数学定义来说明：

从H中任意选择一个方程h，让这个h对样本集合D进行二元分类，输出一个结果向量。例如在平面里用一条直线对2个点进行二元分类，输出可能为{1,–1}，{–1,1}，{1,1}，{–1,–1}，这样每个输出向量我们称为一个dichotomy。

下面是hypotheses与dichotomies(二分法)的概念对比:

如果有N个样本数据，那么有效的假设个数定义为： effective(N) = H作用于样本集D“最多”能产生多少不同的dichotomy。

 

Break Point与Shatter

Shatter的概念：当假设空间H作用于N个input的样本集时，产生的dichotomies数量等于这N个点总的组合数2N是，就称：这N个inputs被H给shatter掉了。

要注意到 shatter 的原意是“打碎”，在此指“N个点的所有(碎片般的)可能情形都被H产生了”。所以mH(N)=2N的情形是即为“shatter”

VC dimension

一个假设空间H的VC dimension，是这个H最多能够shatter掉的点的数量，记为dvc(H)。如果不管多少个点H都能shatter它们，则dvc(H)=无穷大。

根据前面的推导，我们知道VC维的大小：与学习算法A无关，与输入变量X的分布也无关，与我们求解的目标函数f 无关。它只与模型和假设空间有关。

我们已经分析了，对于2维的perceptron，它不能shatter 4个样本点，所以它的VC维是3。此时，我们可以分析下2维的perceptron，如果样本集是线性可分的，perceptron learning algorithm可以在假设空间里找到一条直线，使Ein(g)=0；另外由于其VC维=3，当N足够大的时候，可以推断出：Eout(g)约等于Ein(g)。这样学习可行的两个条件都满足了，也就证明了2维感知器是可学习的。

VC 维与假设参数w 的自由变量数目大约相等。

模型越复杂，VC维大，Eout 可能距离Ein 越远。

除此外，我们为了避免overfit，一般都会加正则项。那加了正则项后，新的假设空间会得到一些限制，此时新假设空间的VC维将变小，也就是同样训练数据条件下，Ein更有可能等于Eout，所以泛化能力更强。

深度学习与VC维

对于神经网络，其VC维的公式为：

dVC = O(VD)，其中V表示神经网络中神经元的个数，D表示weight的个数，也就是神经元之间连接的数目。

举例来说，一个普通的三层全连接神经网络：input layer是1000维，hidden layer有1000个nodes，output layer为1个node，则它的VC维大约为O(1000*1000*1)

可以看到，神经网络的VC维相对较高，因而它的表达能力非常强，可以用来处理任何复杂的分类问题。根据上一节的结论，要充分训练该神经网络，所需样本量为10倍的VC维。如此大的训练数据量，是不可能达到的。所以在20世纪，复杂神经网络模型在out of sample的表现不是很好，容易overfit。

但现在为什么深度学习的表现越来越好。原因是多方面的，主要体现在：

• 通过修改神经网络模型的结构，以及提出新的regularization方法，使得神经网络模型的VC维相对减小了。例如卷积神经网络，通过修改模型结构(局部感受野和权值共享)，减少了参数个数，降低了VC维。2012年的AlexNet，8层网络，参数个数只有60M；而2014年的GoogLeNet，22层网络，参数个数只有7M。再例如dropout，drop connect，denosing等regularization方法的提出，也一定程度上增加了神经网络的泛化能力。
• 训练数据变多了。随着互联网的越来越普及，相比于以前，训练数据的获取容易程度以及量和质都大大提升了。训练数据越多，Ein越容易接近于Eout。而且目前训练神经网络，还会用到很多data augmentation方法，例如在图像上，剪裁，平移，旋转，调亮度，调饱和度，调对比度等都使用上了。
• 除此外，pre-training方法的提出，GPU的利用，都促进了深度学习.

 

有了 VC Dimension 我们就知道了一个假设集合的好坏，那么 VC Dimension 是不是越大越好？比如说我刚才说线性模型的 VC Dimension是 N+1，我们是不是要找一个无限大的 VC Dimension，这样一个假设集合就是最好的？其实并不是的，因为无限大的 VC Dimension 就代表着你会拟合得非常严重。所以说我们引入第二个概念就是 error.