剑指offer刷题记录（六）

最新推荐文章于 2022-07-19 16:06:07 发布

半城抹茶

最新推荐文章于 2022-07-19 16:06:07 发布

阅读量168

点赞数

分类专栏：算法刷题

本文链接：https://blog.youkuaiyun.com/weixin_41938314/article/details/105631304

版权

算法刷题专栏收录该内容

9 篇文章

订阅专栏

解法一：创建一个栈来模拟整个栈的压入和弹出，看看弹出的元素是否和弹出数组中的元素一一对应相等。

代码如下：

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        Stack<Integer> stack = new Stack<>();
        int pushindex = 0;//存入栈内元素的索引
        for(int popindex = 0;popindex<popped.length;popindex++){//控制Stack弹出的次数
            while(pushindex < pushed.length && (stack.isEmpty() || stack.peek() !=popped[popindex])){//模拟的是将pushed数组压入栈的过程
            //首先pushed数组中还有数没被压入，然后stack为空或者stack第一个元素和poped准备弹出的元素不一致
                stack.push(pushed[pushindex]);
                pushindex++;
            }
            if(stack.peek() != popped[popindex]){
                return false;
            }else{
                stack.pop();
            }
        }
        return true;

    }
}

解法二：就是在解法一的基础上优化一下，不再单独弄一个Stack栈来储存了，而是就是pushed数组来实现一个栈，定义一个指针，指向栈顶元素。

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {   
        //用stack指针和原pushed数组模拟一个栈，指针所指即为栈顶元素，其他与上一种解法一致
        //入栈数组的指针，必须维护，才知道此时应该是哪个数入栈
        int stack = -1, pushIndex = 0;
        //遍历要出栈的数组,如果可以全部出栈成功，那么返回TRUE
        for (int poppedIndex = 0; poppedIndex < popped.length; ++poppedIndex) {
            //这个条件很关键，当 还有数可以入栈 && (栈为空，那么直接入栈，或者栈顶元素与要弹出的数不一样，那么继续入栈)
            while (pushIndex < pushed.length && (stack < 0 || pushed[stack] != popped[poppedIndex])) {
                pushed[++stack] = pushed[pushIndex++];
            }
            //能走到这里，要么没有数可以继续入栈了，要么此时的栈顶元素和要弹出的数一致
            //如果栈顶元素和要弹出的数不一致，那么直接返回FALSE，因为正如上面所说，能走到这里还可能是因为没有数可以继续入栈了
            if (pushed[stack] != popped[poppedIndex])
                return false;
            //如果一致，那么出栈
            else 
                --stack;
        }
        //走到这里说明全部出栈成功，那么返回TRUE
        return true;
    }
}

思路：这道题是一道自定义排序的题。首先将Int类型的数组转化为string类型的数组。使用快速排序将string数组排序，只不过排序规则需要自定义。原来Int类型比较大小就是谁小谁在前，直接大于小于符号比较。这里需要定义如下的比较方式：

x+y>y+x（+相当于拼接）说明y更小，x更大。JAVA中字符串大小比较，用compareTo方法

这里如果不能使用内置sort函数的话，那就必须能手写快速排序，并在此基础上修改。

代码思路如下：

基础的快速排序：针对Int数组的排序

public static void quickSort(int [] arr,int left,int right) {
	      int pivot = 0;
	      if(left < right) {
	         pivot = partition(arr,left,right);
	         quickSort(arr,left,pivot-1);
	         quickSort(arr,pivot+1,right);
	      }
}
	
private static int partition(int[] arr,int left,int right) {
 
	      int key = arr[left];
	      while(left < right) {
	         while(left < right && arr[right] >= key) {
	            right--;
	         }
	         arr[left] = arr[right];
	         while(left < right && arr[left] <= key) {
	            left++;
	         }
	         arr[right] = arr[left];
	      }
	      	 arr[left] = key;
	         return left;
 
}

在基础的快排基础上修改成我们的比较规则：

class Solution {
    public String minNumber(int[] nums) {
        String[] str = new String[nums.length];
        for(int i=0;i<nums.length;i++){
            str[i] =String.valueOf(nums[i]);
        }
        int left = 0;
        int right = nums.length-1;
        quicksort(str,left,right);
        StringBuilder res = new StringBuilder();
        for(String a:str){
            res.append(a);
        }
        return res.toString();
        
    }
    public void quicksort(String[] str,int left,int right){
        int pivot = 0;
        if(left < right){
            pivot = helpper(str,left,right);
            quicksort(str,left,pivot-1);
            quicksort(str,pivot+1,right);         
        }

    }
    public int helpper(String[] str,int left,int right){
        String key = str[left];
        while(left < right){
            while(left<right && (str[right]+key).compareTo(key+str[right])>=0) right--;
            str[left] = str[right];
            while(left<right && (str[left]+key).compareTo(key+str[left])<=0) left++;
            str[right] = str[left];
        }
        str[left] = key;
        return left;
    }
}

如果允许使用内置函数：

class Solution {
    public String minNumber(int[] nums) {
        String[] strs = new String[nums.length];
        for(int i = 0; i < nums.length; i++) 
            strs[i] = String.valueOf(nums[i]);
        Arrays.sort(strs, (x, y) -> (x + y).compareTo(y + x));
        StringBuilder res = new StringBuilder();
        for(String s : strs)
            res.append(s);
        return res.toString();
    }
}

思路：前序遍历+回溯法

依次往Path里添加节点的值，然后对目标值tar依次减去每个节点的值，如果最终tar值归0且左右子节点皆为空（已经遍历到叶节点了），就代表目前path里存储的值可以加入到最终结果res里面。依次递归左右节点，如果递归结束，tar依旧不为0，说明这一条支路

class Solution {
    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> path = new LinkedList<>(); 
    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        recur(root, sum);
        return res;
    }
    void recur(TreeNode root, int tar) {
        if(root == null) return;
        path.add(root.val);
        tar -= root.val;
        if(tar == 0 && root.left == null && root.right == null)
            res.add(new LinkedList(path));
        recur(root.left, tar);
        recur(root.right, tar);
        path.removeLast();
    }
}

第一种解法：数学推导（最难想到但是最简单）

为什么切成3是最优的？推导如下：

class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n-1;
        int a = n / 3;
        int b = n - 3*a;
        if(b==0) return (int)Math.pow(3,a);
        if(b==1) return (int)Math.pow(3,a-1)*4;
        return (int)Math.pow(3,a)*2;
    }
}

解法二：动态规划

首先，先递推，找出状态转移方程

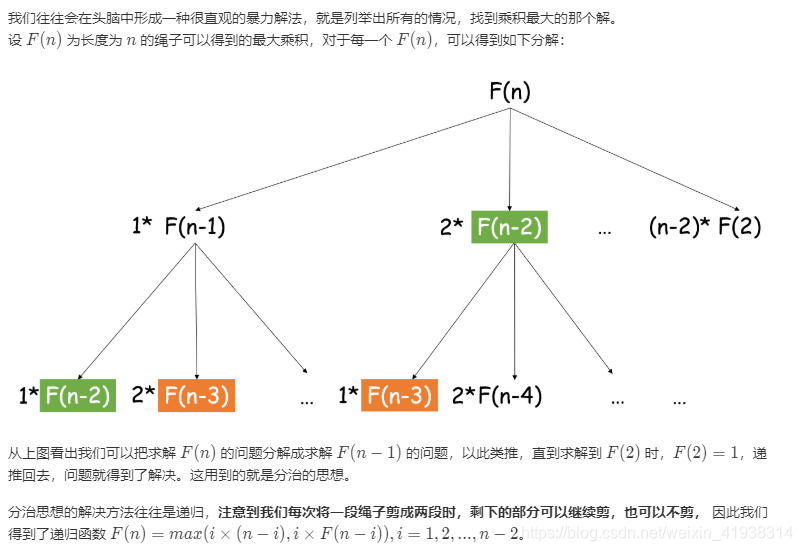
这里为什么最后要和dp[i]求最大值，因为dp[i]的值需要不断被更新,从1*f(n-1),2*f(n-2),3*f(n-3,.......,(n-1)*f(1)之中,挑一个最大的,所以这里的dp[i],其实保留的前一次比较的最大值。

class Solution {
    public int cuttingRope(int n) {
        if (n < 2) {
            return 0;
        }
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j < i; j++) {
                //dp[i] = Math.max(j * dp[i - j], j * (i - j));
                dp[i] = Math.max(Math.max(j * dp[i - j], j * (i - j)), dp[i]);
            }
        }
        return dp[n];
    }
}

这道题使用的是深度优先搜索，难度表较高，比较绕，我是仿真几次才理清了代码思路。

贴上大佬的思路：

代码实现：

class Solution {
    char [] c;//用于存放s中各个字符
    List<String> list = new LinkedList<>();
    public String[] permutation(String s) {
        c = s.toCharArray();//将字符串s转换为字符数组c
        dfs(0);
        return list.toArray(new String[list.size()]);
    }
    //深度搜索方法，实际上参数x代表固定位的索引值
    void dfs(int x){
        //收集满了，可以添加进list中
        if(x == c.length - 1){
            //把c这个字符数组转化为字符串加入到list中
            list.add(String.valueOf(c));
            return ;//判定依据是s字符串最后一位了，所以加入后，dfs这个函数就可以结束了
        }
        HashSet<Character> set = new HashSet<>();//用于存放字符,检验重复性的，并不是把这个set的内容最终加入到list中，作为结果返回
        for(int i=x;i<c.length;i++){
            if(set.contains(c[i])) continue;//如果重复了，不进行交换后续操作了，直接结束
            set.add(c[i]);
            swap(i,x);
            dfs(x+1);//递归调用下一个位，固定下一位
            swap(i,x);//交换回来，为什么要交换回来？
        }
    }
    //交换函数
    void swap(int a,int b){
        char tmp = c[a];
        c[a] = c[b];
        c[b] = tmp;
    }
}

我分析下来，觉得这题挺明显的就是动态规划。

状态转移方程：f(n) = f(n-1)+f(n-2)，这里的n指的是位数

我的初版代码：效率极低

class Solution {
    public int translateNum(int num) {
        String s = String.valueOf(num);
        char[] c = s.toCharArray();
        int [] res = new int[c.length+1];
        if(c.length ==1) return 1;
        res[0] = 0;
        res[1] = 1;
        if((c[0]+""+c[1]).compareTo("25")>0){
            res[2] = 1;
        }else{
            res[2] = 2;
        }
        //if(c.length>=3)
        for(int i=3;i<=c.length;i++){
            if((c[i-2]+""+c[i-1]).compareTo("25")<=0 && (c[i-2]+""+c[i-1]).compareTo("10")>=0){
                //本位和前一位加起来的值比25要小
                res[i] = res[i-1]+res[i-2];

            }else{
                res[i] = res[i-1];
            }
        }
        return res[c.length];
    }
}

我这代码有几个地方可以优化：

1.不需要res这么大的数组，因为f(n)只和f(n-1)、f(n-2)有关，一共三个数，所以完全可以用a,b,c三个数，然后每次循环完对它进行一次更新即可。

2.这里将int类型的num转为string的字符串，后面是没必要转为字符数组，因为后续要用到的地方就是最后2位和10和25比较大小，可以使用substring方法去截取子字符串即可。

所以优化后的代码如下：

class Solution {
    public int translateNum(int num) {
        String s = String.valueOf(num);
        int a = 1, b = 1;
        for(int i = 2; i <= s.length(); i++) {
            String tmp = s.substring(i - 2, i);
            int c = tmp.compareTo("10") >= 0 && tmp.compareTo("25") <= 0 ? a + b : a;
            b = a;
            a = c;
        }
        return a;
    }
}

有一定难度，思想：递归分治本题中13265，可以确定最后一个一定是二叉搜索树的根节点，从头开始遍历，发现的第一个大于根节点的那就是分割线了，左边就是左子树，右边就是右子树。

实现代码：

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        boolean res = recur(postorder,0,postorder.length-1);
        return res;
    }
    public boolean recur(int[] postorder,int i,int j){
        if(i >= j) return true;//初始判断
        int p = i;//i的初始索引
        while(postorder[p] < postorder[j]) p++;//这相当于在遍历左子树
        int m = p;//记录左右子树分割的地方
        while(postorder[p] > postorder[j]) p++;//这相当于在遍历右子树
        return p==j && recur(postorder,i,m-1) && recur(postorder,m,j-1);
    }
}

使用一个队列和一个双向队列可以实现，和前面有一个也是求队列最大值的题目很像，建议复习时一起翻看

class MaxQueue {
    //其实就是要求设计一个队列，能实现3个功能，求最大值、从队列后加入元素、从最前面pop元素
    Queue<Integer> queue;
    Deque<Integer> deque;

    public MaxQueue() {
        //初始化的
        queue = new LinkedList<Integer>();
        deque = new LinkedList<Integer>();//用于储存队列的最大值
    }
    
    public int max_value() {
        if(deque.isEmpty()) return -1;
        return deque.peek();
    }
    
    public void push_back(int value) {
        queue.offer(value);
        while(deque.size() >0 && deque.peekLast() < value){//查询队尾元素
            deque.pollLast();//推出队尾元素
        }
        deque.offerLast(value);
    }
    
    public int pop_front() {
        if(queue.isEmpty()) return -1;
        int pop = queue.poll();
        if(deque.size() >0 && pop == deque.peek()){//查询队首元素
            deque.poll();//推出队首元素
        }
        return pop;
    }
}

/**
 * Your MaxQueue object will be instantiated and called as such:
 * MaxQueue obj = new MaxQueue();
 * int param_1 = obj.max_value();
 * obj.push_back(value);
 * int param_3 = obj.pop_front();
 */

思路：深度优先搜索和广度优先搜索

准备工作：

方法一：深度优先搜索（dfs）

class Solution {
    int m, n, k;
    boolean[][] visited;
    public int movingCount(int m, int n, int k) {
        this.m = m; this.n = n; this.k = k;//这里为什么要写this，因为这里的方法里有m，方法外也有m，同理n,k也是一样，this.m指的是方法外的m，而后面的m指的是参数里的m值。
        this.visited = new boolean[m][n];
        return dfs(0, 0, 0, 0);
    }
    public int dfs(int i, int j, int si, int sj) {
        if(i >= m || j >= n || k < si + sj || visited[i][j]) return 0;
        visited[i][j] = true;
        return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj) + dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8);
    }
}

方法二：广度优先搜索：（bfs），要理解bfs和dfs有何不同之处

class Solution {
    public int movingCount(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        int res = 0;
        Queue<int[]> queue= new LinkedList<int[]>();
        queue.add(new int[] { 0, 0, 0, 0 });
        while(queue.size() > 0) {
            int[] x = queue.poll();
            int i = x[0], j = x[1], si = x[2], sj = x[3];
            if(i >= m || j >= n || k < si + sj || visited[i][j]) continue;
            visited[i][j] = true;
            res ++;
            queue.add(new int[] { i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj });
            queue.add(new int[] { i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8 });
        }
        return res;
    }
}

10.

算法思路：

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if(A == null || B == null) return false;//如果A或者B为空，则返回false
        return (recur(A,B) || isSubStructure(A.left,B) || isSubStructure(A.right,B));//其实这样进行的就是先序遍历
    }
    public boolean recur(TreeNode A, TreeNode B){//判断A,B是否一致
        if(B == null) return true;
        if(A == null || A.val != B.val) return false;
        return (recur(A.left,B.left) && recur(A.right,B.right));
    }
}