nginx数据结构之红黑树（1）_nginx 后端负载红黑树-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_41923293/article/details/113872937

本文介绍了红黑树作为自平衡二叉查找树的特性，对比了普通二叉查找树和AVL树。在二叉查找树的基础上，详细阐述了AVL树的平衡原理及旋转操作，展示了插入和删除节点可能导致的四种失衡情况及对应的旋转修复。红黑树在插入或删除时仅需最多三次旋转即可维持平衡，复杂度为O(1)，适用于频繁插入/删除操作且对查询性能要求不高的场景，例如nginx中的定时器。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

nginx中的定时器实际上就是一颗红黑树，本文主要对红黑树进行一下解读。

红黑树的由来

红黑树是一种自平衡的二叉查找树，提起二叉查找树，每个人都能快速反应过来是什么，下面简单的列出二叉查找树的结点插入与删除方法。

1) 二叉查找树

插入方法：

tree_s * insert_node(tree_s * root, int n)
{
	if(root == NULL)
	{
		root = new tree_s(n);
		return root;
	}
	if(root->value < n)
	{
		root->right = insert_node(root->right, n);
	}
	else
	{
		root->left = insert_node(root->left, n);
	}
	
}

删除方法：
二叉查找树结点的删除相较于插入要麻烦，需要考虑三种情况：
（1）删除的是否是叶子结点，若是叶子结点直接删除，整棵树无需进行调整。
（2）删除的结点是否具有左子树或者右子树，若有，可以将子节点直接移到被删除元素的位置。
（3）删除的结点若既有左子树又有右子树，删除结点时，取待删除几点的左子树最大结点（最右边的结点）或右子树最小结点（最左边结点）与待删除结点进行交换，交换后，删除交换的结点。

//获取左子树最右边叶子结点
tree_s * getmaxnode(tree_s * root)
{
	if(root == NULL)
	{
		return NULL;
	}
	while(root->right)
	{
		root = root->right;
	}
	return root;
}
//获取右子树最左边叶子结点
tree_s * getminnode(tree_s * root)
{
	if(root == NULL)
	{
		return NULL;
	}
	while(root->left)
	{
		root = root->left;
	}
	return root;
}


tree_s * delete_node(tree_s * root, int n)
{
	if(root == NULL)
	{
		return NULL;
	}
	if(root->value == n)
	{
		//叶子结点，直接删除
		if((root->left == NULL) && (root->right == NULL))
		{
			delete root;
			root = NULL;
			return root;
		}
		//左右子树都存在
		else if((root->left != NULL) && (root->right != NULL))
		{
			tree_s * tmp = getmaxnode(root->left);
			root->value = tmp->value;
			//删掉tmp结点，防止tmp含有左子树，仍递归删除
			root->left = delete_node(root->left,tmp->value);
		}
		else if(root->left != NULL)
		{
			tree_s * tmp = root->left;
			delete root;
			root = NULL;
			return tmp;
		}
		else if(root->right != NULL)
		{
			tree_s * tmp = root->right;
			delete root;
			root = NULL;
			return tmp;
		}
	}
	else if(root->value < n)
	{
		root->right = delete_node(root->right);
	}
	else if(root->value > n)
	{
		root->left = delete_node(root->left);
	}
}

2) 平衡二叉树（AVL树）

二叉查找树在一定程度上提升了查找的效率，但在某些特殊的情况下，如一直向根节点的左子树插入结点，会使二叉树退化为一个链表，导致查找的效率下降，即最坏的时间复杂度为O(n),n为结点个数，为了优化这种情况，产生了一种平衡二叉树（AVL），即AVL的左右两颗子树的高度差的绝对值不超过1，其查找的时间复杂度均为O(logn)。

AVL树在插入或者删除结点时，需要检查操作后树是否平衡，若不平衡，需要对失衡的结点进行旋转,树失衡有以下四种情况：
在这里插入图片描述
左左型：在原来平衡的二叉树上，在节点的左子树的左子树下插入一个新节点，需进行单次旋转操作，右旋。
左右型：在原来平衡的二叉树上，在节点的左子树的右子树下插入一个新节点，需进行单两次旋转操作，先对待旋转结点的左孩子进行左旋，再对结点进行右旋。
右左型：在原来平衡的二叉树上，在节点的右子树的左子树下插入一个新节点进行单两次旋转操作，先对待旋转结点的右孩子进行右旋，再对结点进行左旋。
右右型：在节点的右子树的右子树下插入一个新节点，需进行单次旋转操作，左旋。
旋转示例
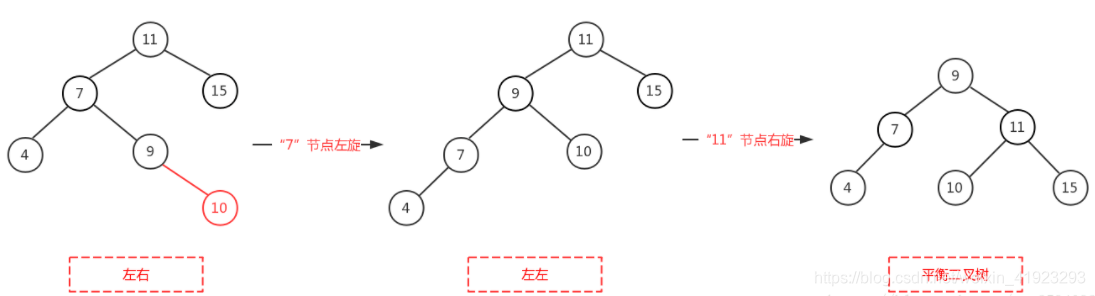
(图片来源自网络，侵删)

旋转代码示例：

int height(tree_s * node)
{
	if(node == NULL)
		return -1;
	return node->height;
}
tree_s * left_rot(tree_s * node)
{
	tree_s * tmp = node->right;
	node->right = tmp->left;
	tmp->left = node;
	//计算调整后的结点高度
	tmp->height =max(height(tmp->left) , height(tmp->left)) + 1;
	node->height = max(height(node->left) , height(node->left)) + 1;
	return tmp;
}

tree_s * right_rot(tree_s * node)
{
	tree_s * tmp = node->left;
	node->left = tmp->right;
	tmp->right = node;
	//计算调整后的结点高度
	tmp->height = max(height(tmp->left) , height(tmp->left)) + 1;
	node->height = max(height(node->left) , height(node->left)) + 1;
	return tmp;
}

//左右旋转的类型，先对结点的孩子进行左旋，再对结点进行右旋
tree_s * lr_rot(tree_s * node)
{
	node->left = left_rot(node->left);
		return right_rot(node);
}

//右左旋转的类型，先对结点的孩子进行右旋，再对结点进行左旋
tree_s * rl_rot(tree_s * node)
{
	node->right = right_rot(node->right);

	return left_rot(node);

}

插入结点;

tree_s * insert_node(tree_s * root, int n)
{
	if(root == NULL)
	{
		root = new tree_s(n);
	}
	if(root->value > n)
	{
		root->left = insert_node(root->left, n);

		//插入结点后，进行平衡检查,因为是插入到左子树，只需检查左子树减去右子树，下方同理

		if(height(root->left) - height(root->right) > 1)
		{
			//左左型
			if(n < root->left->value)
			{
				root = right_rot(root);
			}
			else   //左右型
			{
				root = lr_rot(root);
			}
		}
	}
	else if(root->value < n)
	{
		root->right = insert_node(root->right, n);

		if(height(root->right) - height(root->left) > 1)
		{
			//右右型
			if(n > root->right->value)
			{
				root = right_rot(root);
			}
			else   //右左型
			{
				root = lr_rot(root);
			}
		}
	}
	//重新计算根节点的高度
	root->height = max(height(root->left) , height(root->left)) + 1；
	return root;		
}

删除结点：

tree_s * delete_node(tree_s * root, int n)
{
	if(root == NULL)
	{
		return NULL;
	}
	if(root->value == n)
	{
		//叶子结点，直接删除
		if((root->left == NULL) && (root->right == NULL))
		{
			delete root;
			root == NULL;
			return root;
		}
		//左右子树都存在
		else if((root->left != NULL) && (root->right != NULL))
		{
			//计算左右子树的高度，为尽量保持平衡，删除较高子树上的结点
			if(height(root->left) > height(root->left))
			{
				tree_s * tmp = getmaxnode(root->left);
				root->value = tmp->value;
				//删掉tmp结点，防止tmp含有左子树，仍递归删除
				root->left = delete_node(root->left,tmp->value);
			}
			else
			{
				tree_s * tmp = getminnode(root->right);
				root->value = tmp->value;
				root->left = delete_node(root->right,tmp->value);
			}
			
		}
		else if(root->left != NULL)
		{
			tree_s * tmp = root->left;
			delete root;
			root = NULL;
			return tmp;
		}
		else if(root->right != NULL)
		{
			tree_s * tmp = root->right;
			delete root;
			root = NULL;
			return tmp;
		}
	}
	else if(root->value < n)
	{
		root->right = delete_node(root->right);
		if(height(root->left) > height(root->right) > 1)
		{
			if(height(root->left->left) > height(root->left->right))
			{
				//左左型，右旋
				right_rot(root);
			}
			else
			{
				//左右型
				lr_rot(root);
			}
		}
		else
		{
			root->height = max(height(root->left), height(root->left)) + 1;
		}
	}
	else if(root->value > n)
	{
		root->left = delete_node(root->left);
		if(height(root->right) > height(root->left) > 1)
		{
			if(height(root->right->left) > height(root->right->right))
			{
				//右左型
				rl_rot(root);
			}
			else
			{
				//右右型
				left_rot(root);
			}
		}
		else
		{
			root->height = max(height(root->left), height(root->left)) + 1;
		}
		
	}
}

整体介绍完AVL树后，可发现AVL树在插入或删除结点导致树失衡的情况时，需要维护从被删除结点到根节点整条路径的平衡，因此旋转的复杂度为O(logn)。而接下来要引出的红黑树在结点插入或删除时，最多只需要三次旋转即可维持平衡，复杂度为O(1),在对结点需要进行频繁插入/删除操作时，且对查询的性能要求不高的场景多选用红黑树，如nginx中的定时器，以及STL等。下一节回仔细讲述红黑树的原理，以及与AVL树的差异。