梯度下降法原理和实现

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步一步的迭代求解，得到最小化的损失函数。梯度下降不一定能找到全局的最优解，有可能是一个局部的最优解。当损失函数是一个凸函数时，梯度下降就一定能得到最优解。梯度下降的相关概念有：
步长。步长决定在梯度下降的过程中，每一步沿梯度负方向前进的长度。
特征。指的是样本特征。
假设函数：在监督学习中，为了拟合输入样本，而使用假设函数。
损失函数：为了评估模型的好坏。通常用损失函数来度量拟合的程度。损失函数最小化，意味着拟合程度较好，参数对于模型是最优的。损失函数通常采用假设函数和样本输出的差取平方。
梯度下降详细算法
（1）先决条件
我们可以对假设函数进行一个简化，增加一个特征x0=1, 这样

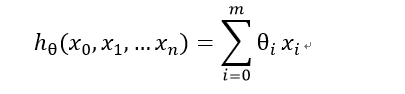
对于上述的假设函数，损失函数为：

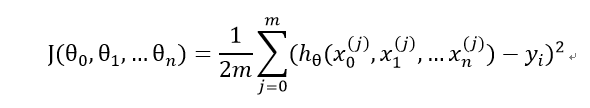
这里的系数不影响取极值时对应的模型参数值，仅影响损失函数的值。我们关心的是对应的模型参数值，所以系数可以根据使求导更加简单易化简的方式自定义。
（2）参数初始化
主要初始化特征参数θ，算法终止距离ε以及步长α。在没有任何先验知识的时候，通常设所有θ为0，步长为1.
（3）算法过程
1.确认损失函数，对θi求偏导。
2.用步长乘以损失函数的梯度，得到当前下降的距离。
3.确认是否所有θ的梯度下降距离都小于ε，如果是则算法终止，当前所有θ即为最终结果，否则进入步骤4。
4.更新所有的θ,对于θi其更新表达式如下，更新完成后继续转入步骤1。
θ_i=θ_i-α ∂/(∂θ_i ) J(θ_0,θ_1,…θ_n)
对梯度下降模拟的代码如下：

import numpy as np
import matplotlib.pyplot as plt
plot_x=np.linspace(