* poj 1062 昂贵的礼物 dijkstra 枚举区间

最新推荐文章于 2019-11-10 15:18:44 发布

duanyuchen

最新推荐文章于 2019-11-10 15:18:44 发布

阅读量159

点赞数

CC 4.0 BY-SA版权

分类专栏：算法 csp考试文章标签：区间枚举 dijkstra 最短路

本文链接：https://blog.youkuaiyun.com/weixin_41894030/article/details/99690739

算法同时被 2 个专栏收录

51 篇文章

订阅专栏

csp考试

47 篇文章

订阅专栏

本文介绍了一个基于最短路径问题的算法解决方案，通过将物品视为节点，将金币交换视为边，解决冒险者如何在有限等级差异下，以最小代价获取酋长承诺的问题。文章详细阐述了Dijkstra算法的应用，以及在具体实现中需要注意的细节。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

思路参考大佬
https://blog.youkuaiyun.com/lyy289065406/article/details/6645852

每个物品看成一个节点，酋长的允诺也看作一个物品，如果一个物品加上金币可以交换另一个物品，
则这两个节点之间有边，权值为金币数，求第一个节点到所有节点的最短路。
因为有等级限制，所以枚举每个点作为最低等级，选取符合所有符合等级限制的点
最短路问题，不过因为存在着等级的差异所以需要枚举一下。本题的思路就是对冒险者的等级进行枚举，也就是说冒险者只能和在他等级以上的人进行交易。这样枚举的好处是能够把所有的情况都考虑进去。有一点需要注意：酋长的等级不一定是最高的
构图时要注意的是，酉长的承诺不是最初的源点，它是一个目标点，也就是说点到点的指向方向是由无替代品的点逐渐指向到酉长的承诺1点，题意说明的是一个回溯的过程，因此可以定义一个最初的源点0点，它到其他各点的权值就是每个物品的原价，而点A到点B的权值就是物品B在有第A号替代品情况下的优惠价
最后，这个题需要注意的一些细节有：
1、初始化的位置，错了就WA了
2、题目中“为了方便起见，我们把所有的物品从1开始进行编号，酋长的允诺也看作一个物品，并且编号总是1。”。也就是说下标从1开始。~~（刚开始我傻了吧唧从0开始，然后出来结果是错的~~
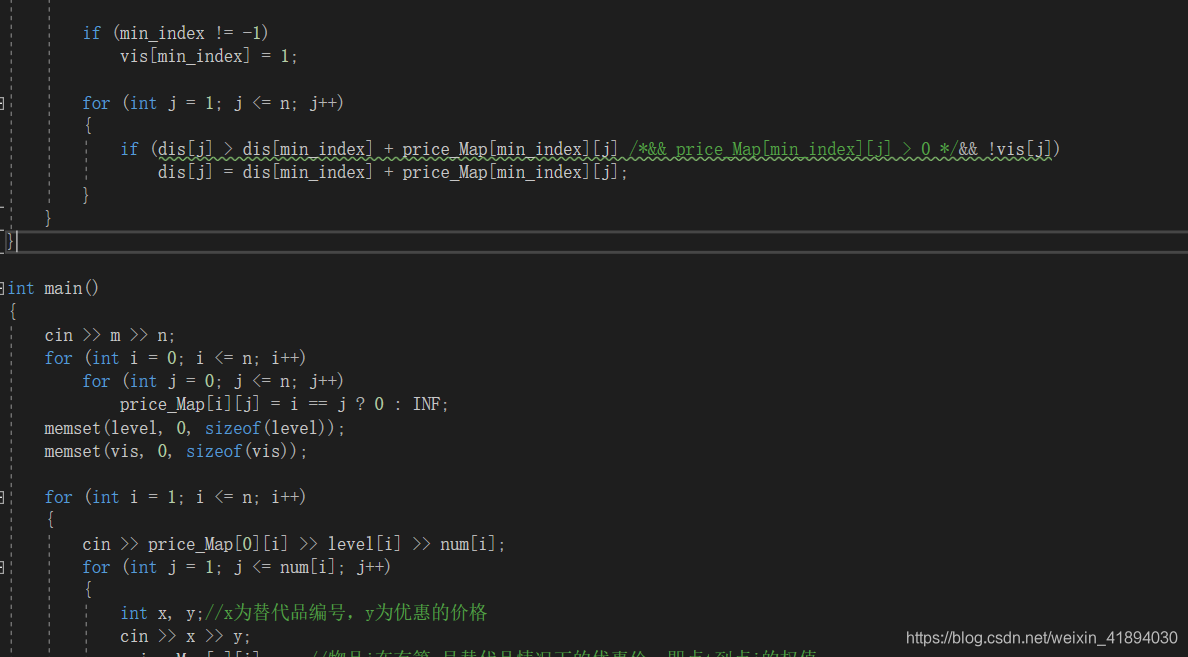
3、dijksta里最后更新的时候，判断条件多了一条，是因为初始化price_Map的时候用的是 memset(price_Map,0,sizeof(price_Map)) ，所以必须加 price_Map[min_index][j] > 0
（参考博客下面第二个代码）

如果按照我的这种写法则不需要多这一个判断（参考博客下面第一个代码）

#pragma warning(disable:4996)
#include<iostream>
#include<string>
#include<cmath>
#include<ctype.h>
#include<memory.h>
#include<string.h>
#include<algorithm>
#include<map>
#include<iomanip>
#include<set>
#include<list>
#include<vector>
#include<stack>
#include<queue>
#define ll long long int
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 110;

int n, m;//n个物体，m为等级差

int price_Map[maxn][maxn];//price_Map[i][j]保存的是物品j在有物品i替换的情况下的价格差（优惠价）
							//当i=0时，说明没有可以替换j的，所以此时为j的原价
int level[maxn];//level[i]表示第i号物品的主任的等级
int num[maxn];//num[i]表示第i号物品的替代品数目

int dis[maxn];//国王要的东西编号为1，dijkstra后要的也就是dis[1]
int vis[maxn];

void dijkstra(int s)
{
	for (int i = 1; i <= n; i++)
		dis[i] = price_Map[s][i];//不可以是price_Map[i][s]！因为price_Map[i][j]的含义限制了
								//后米dijkstra(0)的时候，初始化dis[i]=price_Map[0][i]，代表wupi没有替代品的时候的值（自己的价格

	vis[s] = 1;
	for (int i = 1; i <= n; i++)
	{
		int Min = INF;
		int min_index = -1;
		for (int j = 1; j <= n; j++)
		{
			if (Min > dis[j] && !vis[j])
			{
				Min = dis[j];
				min_index = j;
			}
		}

		if (min_index != -1)
			vis[min_index] = 1;

		for (int j = 1; j <= n; j++)
		{
			if (dis[j] > dis[min_index] + price_Map[min_index][j] /*&& price_Map[min_index][j] > 0 */&& !vis[j])
				dis[j] = dis[min_index] + price_Map[min_index][j];
		}
	}
}

int main()
{
	cin >> m >> n;
	for (int i = 0; i <= n; i++)
		for (int j = 0; j <= n; j++)
			price_Map[i][j] = i == j ? 0 : INF;
	memset(level, 0, sizeof(level));
	memset(vis, 0, sizeof(vis));

	for (int i = 1; i <= n; i++)
	{
		cin >> price_Map[0][i] >> level[i] >> num[i];
		for (int j = 1; j <= num[i]; j++)
		{
			int x, y;//x为替代品编号，y为优惠的价格
			cin >> x >> y;
			price_Map[x][i] = y;//物品i在有第x号替代品情况下的优惠价，即点t到点i的权值
		}
	}

	int min_price = INF;//最低价格(初始化为无限大)
	for (int i = 1; i <= n; i++)
	{/*在等级限制下，寻找允许被当前点访问的点*/
		int limit_level = level[i]; //把当前物品的等级暂时看做最高等级
		for (int j = 1; j <= n; j++)//遍历其他各点
		{
			//当其它物品j的等级比当前物品高(保证单向性)，或者两者等级之差超出限制M时
			if (level[j] > limit_level || limit_level - level[j] > m)
				vis[j] = 1;//物品j则强制定义为“已访问”状态，不参与后续操作
			else
				vis[j] = 0;//否则物品j定义为“未访问”状态，参与后续操作
		}

		dijkstra(0);//从0号点出发，0号没有替代品
		int t_price = dis[1];//记录当前次交易后目标点1在等级lv[i]约束下的最短距离(最少价格)
		min_price = min(min_price, t_price);

		/*cout << "tprice=" << t_price << endl;
		cout << "minprice=" << min_price << endl;
		cout << "level:";
		for (int k = 1; k <= n; k++)
			cout << level[i] << " ";
		cout << endl;

		cout << "dis:";
		for (int k = 1; k <= n; k++)
			cout << dis[i] << " ";
		cout << endl;*/
	}
	cout << min_price << endl;

	return 0;
}

下面这个是乱七八糟的代码

#pragma warning(disable:4996)
#include<iostream>
#include<string>
#include<cmath>
#include<ctype.h>
#include<memory.h>
#include<string.h>
#include<algorithm>
#include<map>
#include<iomanip>
#include<set>
#include<list>
#include<vector>
#include<stack>
#include<queue>
#define ll long long int
using namespace std;
const int INF = 0x3f3f3f3f;
const int maxn = 110;

int n, m;//n个物体，m为等级差

int price_Map[maxn][maxn];//price_Map[i][j]保存的是物品j在有物品i替换的情况下的价格差（优惠价）
							//当i=0时，说明没有可以替换j的，所以此时为j的原价
int level[maxn];//level[i]表示第i号物品的主任的等级
int num[maxn];//num[i]表示第i号物品的替代品数目

int dis[maxn];//国王要的东西编号为1，dijkstra后要的也就是dis[1]
int vis[maxn];

void dijkstra(int s)
{
	//memset(level, 0, sizeof(level));
	//memset(vis, 0, sizeof(vis));
	for (int i = 1; i <= n; i++)
		dis[i] = price_Map[s][i];//不可以是price_Map[i][s]！因为price_Map[i][j]的含义限制了
								//后米dijkstra(0)的时候，初始化dis[i]=price_Map[0][i]，代表wupi没有替代品的时候的值（自己的价格

	vis[s] = 1;
	for (int i = 1; i <= n; i++)
	{
		int Min = INF;
		int min_index = -1;
		for (int j = 1; j <= n; j++)
		{
			if (Min > dis[j] && !vis[j])
			{
				Min = dis[j];
				min_index = j;
			}
		}

		if (min_index != -1)
			vis[min_index] = 1;

		for (int j = 1; j <= n; j++)
		{
			if (dis[j] > dis[min_index] + price_Map[min_index][j] && price_Map[min_index][j] > 0 && !vis[j])
				dis[j] = dis[min_index] + price_Map[min_index][j];
		}
	}
}

int main()
{
	cin >> m >> n;
	for (int i = 0; i <= n; i++)
		for (int j = 0; j <= n; j++)
			price_Map[i][j] = i == j ? 0 : INF;
	//memset(price_Map, 0, sizeof(price_Map));
	memset(level, 0, sizeof(level));
	memset(vis, 0, sizeof(vis));
	//memset(dis, INF, sizeof(dis));

	for (int i = 1; i <= n; i++)
	{
		cin >> price_Map[0][i] >> level[i] >> num[i];
		for (int j = 1; j <= num[i]; j++)
		{
			int x, y;//x为替代品编号，y为优惠的价格
			cin >> x >> y;
			price_Map[x][i] = y;//物品i在有第x号替代品情况下的优惠价，即点t到点i的权值
		}
	}

	int min_price = INF;//最低价格(初始化为无限大)
	for (int i = 1; i <= n; i++)
	{/*在等级限制下，寻找允许被当前点访问的点*/
		int limit_level = level[i]; //把当前物品的等级暂时看做最高等级
		for (int j = 1; j <= n; j++)//遍历其他各点
		{
			//当其它物品j的等级比当前物品高(保证单向性)，或者两者等级之差超出限制M时
			if (level[j] > limit_level || limit_level - level[j] > m)
				vis[j] = 1;//物品j则强制定义为“已访问”状态，不参与后续操作
			else
				vis[j] = 0;//否则物品j定义为“未访问”状态，参与后续操作
		}

		dijkstra(0);//从0号点出发，0号没有替代品
		int t_price = dis[1];//记录当前次交易后目标点1在等级lv[i]约束下的最短距离(最少价格)
		min_price = min(min_price, t_price);

		/*cout << "tprice=" << t_price << endl;
		cout << "minprice=" << min_price << endl;
		cout << "level:";
		for (int k = 1; k <= n; k++)
			cout << level[i] << " ";
		cout << endl;

		cout << "dis:";
		for (int k = 1; k <= n; k++)
			cout << dis[i] << " ";
		cout << endl;*/
	}
	cout << min_price << endl;

	return 0;
}