【2019 牛客多校第九场 Quadratic equation 】

最新推荐文章于 2020-10-11 12:14:02 发布

MatrixYg

最新推荐文章于 2020-10-11 12:14:02 发布

阅读量262

点赞数 1

CC 4.0 BY-SA版权

分类专栏：数学

本文链接：https://blog.youkuaiyun.com/weixin_41863129/article/details/99655313

数学专栏收录该内容

64 篇文章

订阅专栏

本文介绍了一种在模意义下解决一元二次方程的方法，利用韦达定理和勒让德符号，通过构造二次域进行快速幂运算，实现对特定形式方程的有效求解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.题面：

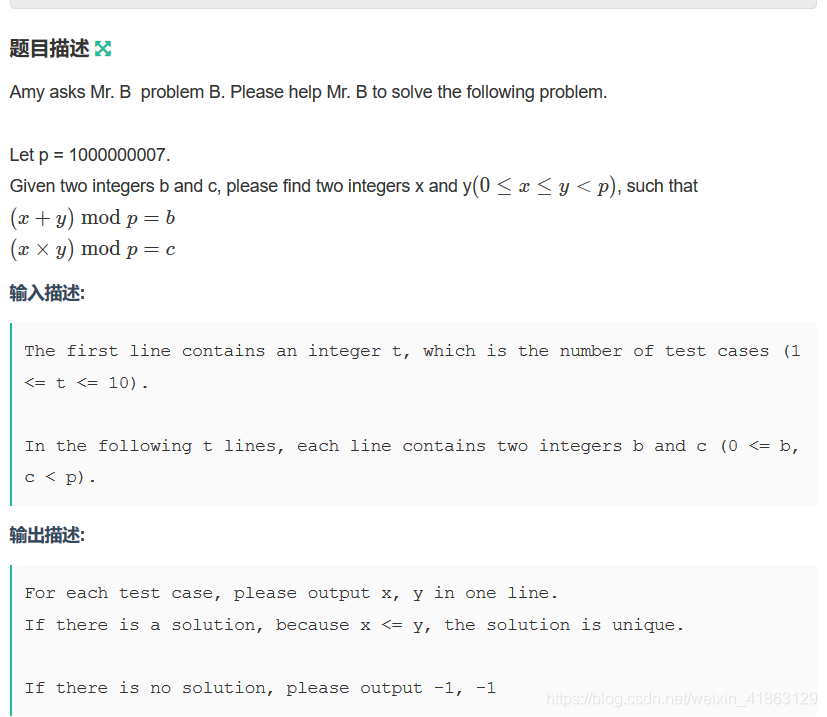
题意十分解明了。仔细观察这个式子，可以发现这个式子就是韦达定理。我们构造一个模意义下的二次函数，然后在这个模意义下解一下这个方程就好了。其实这就涉及到模意义下的一元二次方程怎么解的问题？和一般的解法是一样的，有解和无解的判断条件就是看一下delt是不是存在二次剩余，如果存在那么就求根公式上了，如果不存在就无解。

#include <iostream>
#include <ctime>
using namespace std;
typedef long long LL;
#define random(a,b) (rand()%(b-a+1)+a)
LL quick_mod(LL a, LL b, LL c) { LL ans = 1; while (b) { if (b % 2 == 1)ans = (ans * a) % c; b /= 2; a = (a * a) % c; }return ans; }

LL p = 1e9 + 7;
LL w;//二次域的D值
bool ok;

struct QuadraticField//二次域
{
	LL x, y;
	QuadraticField operator*(QuadraticField T)//二次域乘法重载
	{
		QuadraticField ans;
		ans.x = (this->x * T.x % p + this->y * T.y % p * w % p) % p;
		ans.y = (this->x * T.y % p + this->y * T.x % p) % p;
		return ans;
	}
	QuadraticField operator^(LL b)//二次域快速幂
	{
		QuadraticField ans;
		QuadraticField a = *this;
		ans.x = 1;
		ans.y = 0;
		while (b)
		{
			if (b & 1)
			{
				ans = ans * a;
				b--;
			}
			b /= 2;
			a = a * a;
		}
		return ans;
	}
};

LL Legender(LL a)//求勒让德符号
{
	LL ans = quick_mod(a, (p - 1) / 2, p);
	if (ans + 1 == p)//如果ans的值为-1，%p之后会变成p-1。
		return -1;
	else
		return ans;
}

LL Getw(LL n, LL a)//根据随机出来a的值确定对应w的值
{
	return ((a * a - n) % p + p) % p;//防爆处理
}

LL Solve(LL n)
{
	if (n == 0) { ok = true; return 0; }
	LL a;
	if (p == 2)//当p为2的时候，n只会是0或1，然后0和1就是对应的解
		return n;
	if (Legender(n) == -1)//无解
		ok = false;
	srand((unsigned)time(NULL));
	while (1)//随机a的值直到有解
	{
		a = random(0, p - 1);
		w = Getw(n, a);
		if (Legender(w) == -1)
			break;
	}
	QuadraticField ans, res;
	res.x = a;
	res.y = 1;//res的值就是a+根号w
	ans = res ^ ((p + 1) / 2);
	return ans.x;
}
typedef long long ll;
ll pow_mod(ll a, ll b)
{
	ll res = 1;
	while (b > 0)
	{
		if (b & 1)res = res * a % p;
		a = a * a % p;
		b >>= 1;
	}
	return res;
}
ll inv(ll a)
{
	return pow_mod(a, p - 2);
}
int main() 
{
	int inv2 = inv(2);
	int t; scanf("%d", &t);
	while (t--) {
		int b, c; scanf("%d%d", &b, &c);
		int dalt = (1ll * b * b - 4ll * c % p + p) % p;
		ok = true;
		int ans1 = Solve(dalt);
		if (!ok)
		{
			printf("-1 -1\n");
			continue;
		}
		int x = 1ll * (b + ans1) * inv2 % p;
		int y = 1ll * (b - ans1 + p) * inv2 % p;
		if (x > y)swap(x, y);
		printf("%d %d\n", x, y);
	}
	return 0;
}