归并排序（Merge Sort）

1 前言

冒泡排序、插入排序、选择排序这三种算法的时间复杂度都为 $O(n^2)$，只适合小规模的数据。归并排序（Merge Sort）和快速排序（Quick Sort）的时间复杂度为 $O(nlogn)$ ，用到了分治思想。

时间复杂度： $O(nlogn)$
空间复杂度： $O(n)$
是否稳定： 稳定

2 归并排序

2.1 核心思想

如果要排序一个数组：

1. 先把数组从中间分成前后两部分；
2. 然后分别对前后两部分进行排序；
3. 再将排好序的两部分数据合并在一起。
   
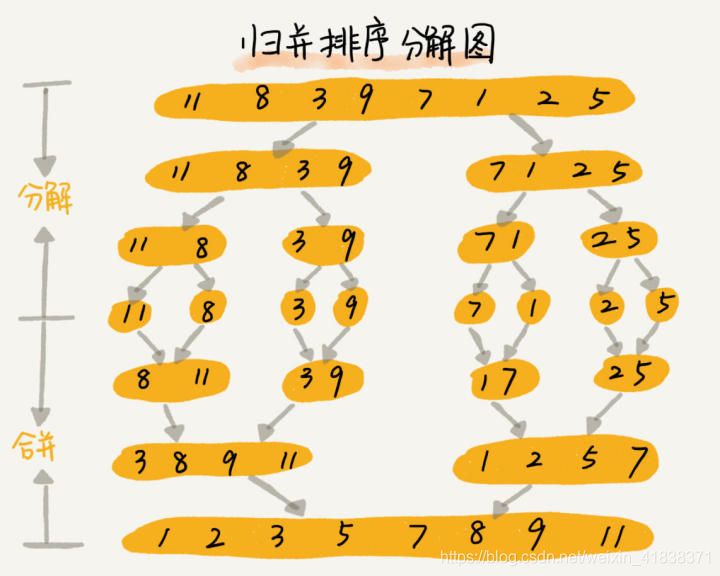
   归并排序使用的是分治思想，也即是分而治之，将一个大问题分解为小的子问题来解决。
   分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧。

2.2 算法思路

如果要对数组区间 [p, r] 的数据进行排序，

1. 先将数据拆分为两部分 [p, q] 和 [q+1, r]，其中 q 为中间位置。
2. 对两部分数据排好序后，我们再将两个子数组合并在一起。
3. 当数组的起始位置大于等于终止位置 $p>=r$ 时，说明此时只有一个或者少于一个元素，递归也就结束了。

递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))

终止条件：
p >= r 不用再继续分解

对两个子数组进行 合并（Merge函数） 的过程如下所示，

1. 先建立一个临时数组，
2. 然后从两个子数组的起始位置开始比较，将较小的元素一个一个放入临时数组，直到其中一个子数组比较完毕，
3. 再将剩下的另一个子数组余下的值全部放到临时数组后面。
4. 最后我们需要将临时数组中的数据拷贝到原数组对应的位置。

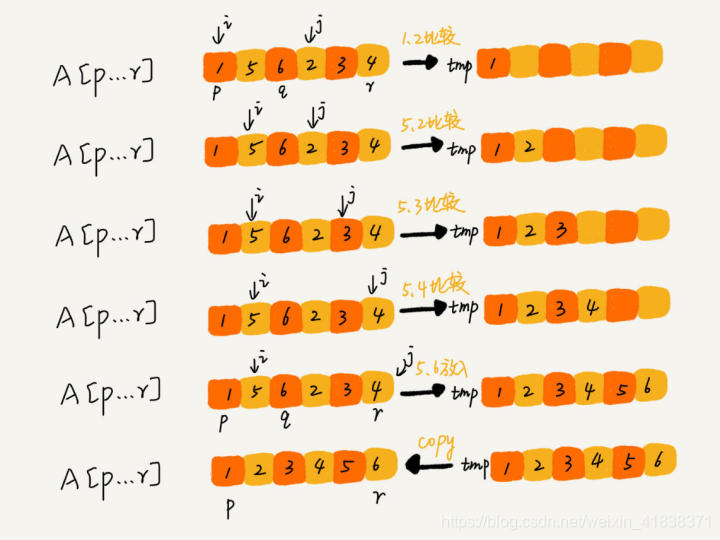
2.3 算法实现

合并两个有序数组，与LeetCode88.合并两个有序数组类似，但是该题目已经分配了合并之后数组的存储空间，而归并排序算法需要开辟一个临时数组空间。
合并代码：

def Merge(left,right):
	"""
	input: Two sorted number sets
	"""
    r, l=0, 0
	result=[]
    while l<len(left) and r<len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    # 此处无需判断哪个数组到达了终点，直接进行数组相加即可。
    result += right[r:]
    result += left[l:]
    return result

归并排序递归写法：

def MergeSort(lists):
    if len(lists) <= 1:
        return lists
    # 对半分割，然后排序
    num = int( len(lists)/2 )
    left = MergeSort(lists[:num])
    right = MergeSort(lists[num:])
    return Merge(left, right)

主函数：

print MergeSort([1, 2, 3, 4, 5, 6, 7, 90, 21, 23, 45])

2.3 算法分析

1. 归并排序是一个稳定的排序算法，在进行子数组合并的时候，我们可以设置当元素大小相等时，先将前半部分的数据放入临时数组，这样就可以保证相等元素在排序后依然保持原来的顺序。
2. 时间复杂度: 不仅递归求解的问题可以写成递推公式，递归代码的时间复杂度也可以写成递归公式。

解释一：设数列长为 n，将数列分开成小数列一共要 $logn$ 步，每步都是一个合并有序数列的过程，时间复杂度可以记为 $O(n)$，故一共为 $O(nlogn)$。
解释二：如果我们对 $n$ 个元素进行归并排序所需要的时间是 $T(n)$，那分解成两个子数组进行归并排序的时间都是 $T(\frac{n}{2})$ ，而合并两个子数组的时间复杂度为 $O(n)$。 所以，归并排序的时间复杂度计算公式为：
$$T(1)=C;$$

$n=1$ 时，只需要常量级的执行时间，所以表示为 $C$，即 $T(1)=C$。
$$T(n)=2\ast T(\frac{n}{2})+n,n>1$$

$T(n)$ 的递归推导如下：
$$\begin{gathered} T(n)=2\ast T(\frac{n}{2})+n \\ =2\ast [2\ast T(\frac{n}{4})+\frac{n}{2}]+n \\ =4\ast T(\frac{n}{4})+2\ast n \\ =4\ast [2\ast T(\frac{n}{8})+\frac{n}{4}]+2\ast n \\ =8\ast T(\frac{n}{8})+3\ast n \\ ...... \\ =2^k\ast T(\frac{n}{2^k})+k\ast n \end{gathered}$$
当 $\frac{n}{2^k}=1$ 时，$k=lo{g}_{2}n$ ，代入上式得：$T(n)=n\ast C+nlo{g}_{2}n$ 用大 $O$ 标记法来表示，归并排序的时间复杂度为 $O(nlogn)$。

从我们的分析可以看出，归并排序的执行效率与原始数据的有序程度无关，其时间复杂度非常稳定，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 $O(nlogn)$。

3. 归并排序有一个缺点，那就是它不是原地排序算法。在进行子数组合并的时候，我们需要临时申请一个数组来暂时存放排好序的数据。因为这个临时空间是可以重复利用的，因此归并排序的空间复杂度为O(n)，最多需要存放n个数据。

参考：

1. https://zhuanlan.zhihu.com/p/47067858