leetcode整数题思路

最新推荐文章于 2025-04-21 22:09:55 发布

原创最新推荐文章于 2025-04-21 22:09:55 发布

· 483 阅读

0 ·

版权

文章标签：

#leetcode #算法

leetcode 专栏收录该内容

8 篇文章

订阅专栏

本文详细解析了LeetCode中涉及位操作的算法题，包括整数除法、二进制加法、前n个数字二进制中1的个数、只出现一次的数字以及单词长度的最大乘积。讲解了如何使用位运算优化算法，降低时间复杂度，如通过位移操作实现整数除法，位与操作寻找只出现一次的数字等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 整数除法

在这里插入图片描述
链接：整数除法（简单）

解：

该题如果要实现不用乘法和除法实现整数除法，那就只能用减法去做，用被除数减除数的方式。当然，让a循环减b的方法，时间复杂度会比较大。那么，我们可以让a减b的倍数，这样能大大减少计算量。

22 - 3 * 8 < 0 
22 - 3 * 7 > 0

如同上面的例子，此时就知道结果是7。但如果还是循环这个倍数，那就和循环减b没什么区别了。

此时我们可以用位运算的方法：当一个数左移一位时，表示这个数乘以2；当一个数右移一位时，表示这个数除以2。那么，我们就可以每次让a - (b的左移后的数)，并判断大小。

这种方法和前一种方法类似，所以用位运算的方法就避免了到临界点的n次，而是循环固定的31次（移位运算在int中有效的次数只有31次），时间复杂度由O(n)变成了O(1)。

这里，我们设置被减数和减数分别为a和b，当次的倍数为k。 

b = (3 << 3) = 3 * 2^3 = 24, 此时k = 2^3
a - b = 22 - (3 << 3)  = -2 < 0, 无法减去。

b = (3 << 2) = 3 * 2^2 = 12, 此时k = 2^2 = 4
a - b = 22 - (3 << 2)  = 10, 可以减去。 更新： a = 10, i  = i + k = 4。 

b = (3 << 1) = 3 * 2^1 = 6, 此时k = 2^1 = 2
a - b = 10 - (3 << 1)  = 4, 可以减去。 更新： a = 4, i  = i + k = 6。 

b = (3 << 0) = 3 * 2^0 = 3, 此时k = 2^0 = 1
a - b = 4 - (3 << 1)  = 1, 可以减去。 更新： a = 1, i  = i + k = 7。 

a < b, 结束。 i = 7，符合结果。

这里需要注意，倍数从上往下会比从下往上要更快，因为从下往上每次都需要从头开始上，而从上往下时，每次减完的a一定会更小，所以只需要一路向下算即可。

// 时间复杂度：O(1)
public int divide(int a, int b) {
	//这里解决-2147483648 / -1 的特例
    if (a == Integer.MIN_VALUE && b == -1)
        return Integer.MAX_VALUE;
    int sign = (a > 0) ^ (b > 0) ? -1 : 1;
    a = Math.abs(a);
    b = Math.abs(b);
    int res = 0;
    for (int i = 31; i >= 0; i--) {
        // 首先，这里为了避免b左移越界，所以使用a右移的方式，a/2和b*2在这里等效
        // 右移的话，再怎么着也不会越界
        // 其次，无符号右移（>>>）的目的是：将 -2147483648 看成 2147483648
        // 因为已经取绝对值，所以不用担心无符号右移的正负问题

        // 注意，这里不能是 (a >>> i) >= b 而应该是 (a >>> i) - b >= 0
        // 这个也是为了避免 b = -2147483648，如果 b = -2147483648
        // 那么 (a >>> i) >= b 永远为 true，但是 (a >>> i) - b >= 0 为 false
        if ((a >>> i) - b >= 0) { // a >= (b << i)
            a -= (b << i);
            res += (1 << i);
        }
    }
    // bug 修复：因为不能使用乘号，所以将乘号换成三目运算符
    return sign == 1 ? res : -res;
}

2 二进制加法

在这里插入图片描述
链接：二进制加法（简单）

class Solution {
    public String addBinary(String a, String b) {
        int aIndex = a.length()-1, bIndex = b.length()-1;
        int carry = 0, retNum = 0;
        StringBuilder sb = new StringBuilder();
        while(aIndex>=0 || bIndex>=0 || carry==1){
            int aNum = aIndex >=0 ? (a.charAt(aIndex) - '0') : 0;
            int bNum = bIndex >=0 ? (b.charAt(bIndex) - '0') : 0;
            retNum = (carry + aNum + bNum) % 2;
            carry = (carry + aNum + bNum) / 2;
            sb.append(retNum);

            aIndex--;
            bIndex--;
        }
        return sb.reverse().toString();
    }
}

这里有几个注意点：

char型转int型，只需要将（字符-‘0’）即可；同样，int转char型也只要将（数字+‘0’）即可。当然，前提是变量的类型先决定。
做字符串的加法的时候，跟链表排序是不太一样的，并不需要循环出短的一头，再将长的剩余字符串直接拼接头，因为这样进位运算会很麻烦。可以直接将短的那一头赋0，能达到相同目的。
使用StringBuilder来append，比一直用String覆盖的计算量要小很多。

3. 前 n 个数字二进制中 1 的个数

在这里插入图片描述
链接：前 n 个数字二进制中 1 的个数（简单）

使用位数运算，使用x & (x - 1)的方法使得二进制位数最低的1置0。但是这种方法时间复杂度很大，为O(nlogn)。

public int[] countBits(int n) {
    int[] ret = new int[n+1];
    for(int i = 1; i<=n; i++){
        int x = i;
        while(x>0){
        	x = x & (x - 1);
        	ret[i]++;
		}	
    }
    return ret;
}

要想用O(n)的时间复杂度解题，就需要用动态规划的手段。

首先，动态规划的思想就是将一个大问题拆成一堆小问题，并且通过小规模的子问题的解推导出大规模的子问题，或者说利用前面的小问题的解来解出后面小问题的解。

我们假设有一个非负整数n，当我们做for循环一次遍历0~n个数时，总是会遍历到2的整数次幂的数。对于正在遍历的正整数i，假设其中一个最大的正整数x，x<=i且x为2的整数次幂，那么x的二进制数一定只有一个最高位为1，其余位为0。
我们用bitcount[i]来表示i的二进制中1的位数，那么我们可以得出，bitcount[i] = bitcount[i-x] + bitcount[x] = bitcount[i-x] + 1。这就是状态转换方程。
至于如何在遍历过程中找到哪个值是x，我们可以用计算x & (x-1)的方法。当x & (x-1)==0时，也就是指x只有最高位有一个1，其余都为0。满足2的整数次幂的条件。

public int[] countBits(int n) {
    int[] ret = new int[n+1];
    ret[0] = 0;
    int high = 0;
    for(int i = 1; i<=n; i++){
        //如果i是2的整数次幂，即最高位为1其余为0
        if((i & (i-1)) == 0){
            //此时i为最高位数
            high = i;
        }
        ret[i] = ret[i-high] + 1;
    }
    return ret;
}

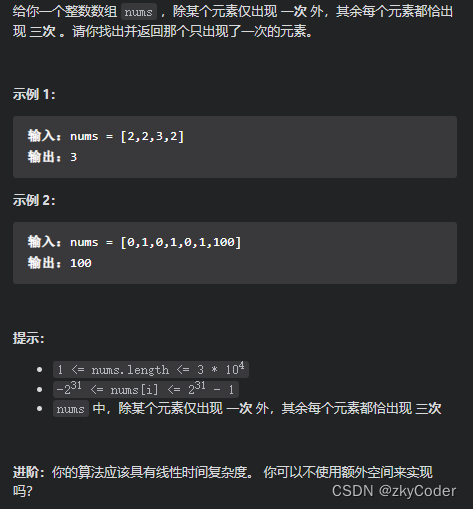
4. 只出现一次的数字

在这里插入图片描述
链接：只出现一次的数字（中等）

这道题最直观的方式就是使用map来记录每个数的数量，然后遍历map找到数量为1的key。但是如果要求不用额外空间来实现的话，就需要其他方法。

这里可以使用位运算的方法。对于恰好出现三次的数字，其二进制数也是一样的，要么都是0要么都是1。所以如果所有数都出现了三次，对于某个二进制位i，所有数字的和一定是可被3整除。
既然如此，如果那个只出现了一次的数在i位上的值是1，这个和就不会被3整除，也就是说，如果我们遍历找到bitCount%3!=0的值，那么只出现一次的数在i位的值为1。以此类推，我们就可以得到这个数的整个二进制数。

public int singleNumber(int[] nums) {
    int ret = 0;
    //对所有数的每一位做遍历
    for(int i = 0; i<32; i++){
        int bitCount = 0;
        for(int num : nums){
            //如果该位不为0则记录下来
            bitCount += (num>>i) & 1;
        }
        //出现三次的数的位数值和一定为0或3
        if(bitCount%3!=0){
            ret += (1 << i);
        }
    }
    return ret;
}

5.单词长度的最大乘积

在这里插入图片描述
链接：单词长度的最大乘积（中等）

这道题最直接的方法就是两两单词对单词内的字母做匹配，关键是我们是否可以把匹配的方法优化，如果单词与单词的匹配时间复杂度为O(1)，那么算法的时间复杂度就可以优化成O(n^2)。

因为这里不需要考虑字符串的顺序，所以我们只需要记录字母是否出现即可。在匹配的时候，我们可以不用每个字母逐一匹配，而是用一个数的二进制位来做标记。一个字符串由一个数的二进制数来表示，这个数的低位开始的26位表示这个字符串是否有对应的26个字符。

这样，在进行匹配的时候，只要判断两个字符串的数的逻辑与（&）是否为0，就知道两个单词是否有重复的字母了。

public int maxProduct(String[] words) {
    int[] bitCount = new int[words.length];
    //对每一个字符串的每一个字母
    for(int i = 0; i< words.length; i++){
        String word = words[i];
        //用bitCount[i]的后26位记录字母是否存在
        //取|而不是取累加是因为同一个字符串中可能会有多个相同的字母
        //我们只记录一个，否则匹配时可能会出现都不为0但不相等的情况
        for(int j = 0; j<word.length(); j++){
            bitCount[i] |= (1 << (word.charAt(j) - 'a'));
        }
    }

    int maxNum = 0;
    for(int i = 0; i<bitCount.length; i++){
        for(int j = i + 1; j<bitCount.length; j++){
            if((bitCount[i] & bitCount[j]) == 0){
                int temp = words[i].length() * words[j].length();
                maxNum = temp > maxNum ? temp : maxNum;
            }
        }
    }
    return maxNum;
}