（剑指offer）刷LeetCode（1）

剑指offer04：二维数组中的查找

思考过程：首先这个数组有一个特征就是，从左到右，从上到下是递增的，第一反应就是从左上角开始找，但是判定过程中就会遇到两条路都能走的情况：我是往上走，还是往右走？没有一个明显的判定条件来决策行动。

所以换个思路，从右上角开始查找：如果当前元素值比target小，就往下走，如果当前元素值比target大，就往左走

代码书写过程中遇到的问题：首先要获取二维数组的行列，怎么获取有两种，一种是导库，

import numpy as np
print x.shape 
# 只输出行数
print x.shape[0] 
# 只输出列数
print x.shape[1] 

面试尽量避免导库所以pass，一种是求数组长度

len(arr) #行数
len(arr[0])　#列数

代码过程中要注意的点：右上角的行列值；往左走是变列，往下走是变行；行增加，列减少；行列下标索引是长度-1

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        # 特殊情况
        if not matrix:
            return False
        # 获取行列，用于所以，从0开始遍历到长度-1
        rows = len(matrix)-1
        cols = len(matrix[0]) - 1 #列数
        #右上角
        i = 0  #右上角行为0
        j = cols  #列为最后一列
        while i<=rows and j>=0:
            if target<matrix[i][j]: #比target大往左走，列减少
                j -= 1
            elif target>matrix[i][j]: #比target小往下走，行增加
                i += 1
            else:
                return True
        return False

剑指offer05：替换空格

class Solution:
    def replaceSpace(self, s: str) -> str:
        new_str = '' #定义一个新的空字符串
        for str in s:
            if str ==' ':
                new_str = new_str +'%20' #如果旧字符串中是空格，添加到新字符串后就是%20
            else:
                new_str = new_str+str   #不是空格的旧字符串直接加进去
        return new_str #返回新的字符串

剑指offer06：从尾到头打印链表

因为链表只能从头到尾的遍历，所以考虑在遍历过程中把每一个元素放到栈中，然后输出栈就是一个逆序的结果了。

class Solution:
    def reversePrint(self, head: ListNode) -> List[int]:
        # 建一个栈
        stack = []
        #res列表保存结果
        res = []
        # 定义一个指针指向链表
        p = head
        #遍历链表，把元素放到栈中
        while p:
            stack.append(p.val)
            p = p.next
         #遍历栈，弹出放到结果集中
        while stack:
            a = stack.pop()
            res.append(a)
         #返回结果
        return res

剑指offer07：重建二叉树

已知二叉树的中序遍历，跟其他一种二叉树的遍历都能重构二叉树，但是如果没有中序遍历，其他的两两组合是构建不出来的。而先序遍历和中序遍历的关系是先序的第一个元素时树的根节点，对应到中序遍历中就可以区分出根节点的左右子树，左右子树再对应到先序又可得到各自的根，对应到中序又可得到各自的左右子树，所以这道题采用递归。递归终止的条件为某一序列遍历完毕。
递归的写法：先一般（递归的主题部分），再特殊（递归的边界）；每次调用需缩小问题规模，对于函数的编写，从上到下分为三个部分：

第一部分：编写递归到底的处理逻辑（此时不用调用自己）

第二部分：编写未递归到底的处理逻辑

第三部分：编写返回上一层调用时需要的处理逻辑

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        # 递归最后的处理
        if  not preorder or not inorder :
            return 
        # 递归结束之前的逻辑
        root = TreeNode(preorder[0])   # 在pre中获取根节点
        i= inorder.index(preorder[0])  # 在in中找到跟结点
        # 左右子树调用函数自身
        root.left =self.buildTree(preorder[1:i+1],inorder[:i]) # 左子树前序到i之前，中序到i之前
        root.right =self.buildTree(preorder[i+1:],inorder[i+1:]) # 右子树对i之后遍历
        return root

剑指offer09：用两个栈实现队列

要求用栈实现队列的入队和出队操作,定义两个栈;入队和入栈一样，都在尾部操作；
出队需要把元素转移到另一个栈，另一个栈的顶元素为原来栈的尾部元素，弹出栈顶元素后剩余元素再放第一个栈。
更新：一开始出队的想法是两个栈直接来回倒，这样无谓的元素倒换太浪费了，所以压进第二个栈取出栈顶元素后不再倒回去，当第二个栈没空的时候就从第二个栈顶取出队元素，当第二个栈空的时候就把第一个栈的元素压入然后弹出栈顶元素

class CQueue:

    def __init__(self):
        # 定义两个栈，继承self
        self.stack_in = [] #实现入队
        self.stack_out = [] # 实现出队


    def appendTail(self, value: int) -> None:
        self.stack_in.append(value) #入队直接在栈尾操作，一样的



    def deleteHead(self) -> int:
        if self.stack_out:  #如果出队的栈不空，直接弹出
            return self.stack_out.pop()
        if not self.stack_in: # 如果出队的栈空，入队的栈也没元素放到出队的中了，返回-1
             return -1
        while self.stack_in: # 如果出队的栈空，入队的栈没空，把入队的栈元素放到出队栈，弹出
            self.stack_out.append(self.stack_in.pop())
        return self.stack_out.pop()

剑指offer11：旋转数组中的最小数字

这个题目的意思是给一个递增序列生成的的旋转数组，不需要我们先旋转再找最小值，一开始还以为要先旋转。
先观察旋转数组的特点，本来是一个递增的序列[1,2,3,4,5],旋转后成为[3,4,5,1,2]，可以看到发生旋转的前后两部分内部依然是一个递增关系[3,4,5][1,2]，但是衔接的地方乱序了[5,1]。而且旋转后前面的数组大于后面的数组。
我们可以找中心点，有两种情况，一种是[3,4,5][1,2]，中间元素大于最右元素，此时最小元素在后半部分；一种是[4,5][1,2,3]，中间元素小于最右元素，此时最小元素在前半部分.

class Solution:
    def minArray(self, numbers: List[int]) -> int:
        left = 0
        right = len(numbers)-1
        while left<right:
            mid = (left+right)//2
            if numbers[mid]>numbers[right]:
                left = mid+1
            elif numbers[mid]==numbers[right]:
                right-=1
            else:
                right = mid
        return numbers[left]

此题思路传送门

剑指offer10-1：斐波那契数列

首先想到递归，但是运行超时，因为包含大量的重复计算。

class Solution:
    def fib(self, n: int) -> int:
        if (n < 2):
            return n
        return self.fib(n - 1) + self.fib(n - 2)

随着N的正常，二叉树也越来越庞大，算法复杂度达到2^n。

计算n=5，进行了n-1层计算，所以需要循环n-1次，里面做加法。如果令小的数是a,大的数是b，每增加一层，小的数变成a = b，大的数变成b= a+b，依次类推.上一次的结果作为下一次的输入。

class Solution:
    def fib(self, n: int) -> int:
        if n==0:
            return 0
        if n==1:
            return 1
        a = 0
        b = 1
        ret = 0
        for i in range(1,n-1):
            ret = a+b
            a = b 
            b = ret
        return ret

剑指offer10-2：青蛙跳台阶

暴力法：找规律，发现符合斐波那契数列。
第二种方法，倒着找规律。假设现在青蛙在n层台阶上，它跳上这层台阶之前有两种选择，跳1步或者跳2步，如果是跳1步，在这之前还有f（n-1）种选择，如果是跳2步，在这之前还有f（n-2）种选择。并且可以得到边界条件n=1和n=2时不能运用f(n)=f(n-1)+f(n-2)的计算公式，要单独判断。

class Solution:
    def numWays(self, n: int) -> int:
        if n < 1:
            return 1 
        if n ==1:
            return 1
        if  n==2:
            return 2
        ret = 0
        a = 1
        b = 2
        for i in range(3,n+1):
            ret = a+b
            a = b
            b = ret
        return ret

剑指offer：变态跳台阶

在LeetCode上没搜到题号，这里先重述一下题干：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路：参考上一题，从最后倒着推。假设此时青蛙到了第n级台阶，有1,2，……n种跳法，如果是跳一步上来的，前面还有f(n-1)；如果是跳2步上来的，前面还有f(n-2)种，以此类推，如果是跳n步上来的，就是f(n-n)：
n = n时：
f(n) = f(n-1)+f(n-2)+…+f(n-(n-1)) + f(n-n) = f(0) + f(1) + f(2) + … + f(n-1)
由于
f(n-1) = f(0)+f(1)+f(2)+ … + f((n-1)-1) = f(0) + f(1) + f(2) + f(3) + … + f(n-2)
所以
f(n) = f(n-1)+f(n-1)=2*f(n-1)

class Solution:
    def rectCover(self, number):
        if number <= 0: return 0
        if number == 1: return 1
        if number == 2: return 2
        result = [1,2]
        for i in range(2,number+1):
            result.append(2*result[-1])
        return result[-1]

剑指offer12：矩阵中的路径

首先：需要明确矩阵中允许重复元素存在，但不允许读取相同的元素，除非你读取的是不同位置的同字母。结题思路参考回溯

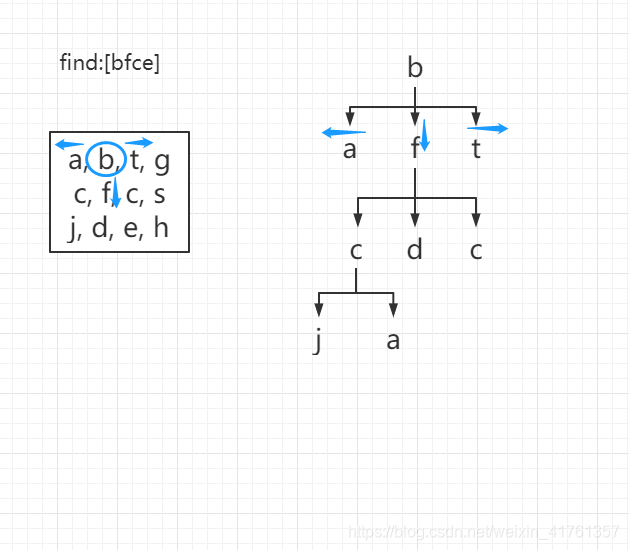
第一个字母b，找其上下左右元素为a,f,t，

a不符合要求，返回上一级，找到f，符合。
接下来找f后面的c，f的上下左右为c,d,c由于上面的b已经遍历过了所以不参与选择

找左边的c，符合条件，接下来找c后面的e，发现c后面找不到e,此路不通，返回上一级，找d，不符合，找c，右边c符合，接下来找e


用到了dfs思想，所以需要写出dfs，过程中我们还需要多字符串中找的第几个字符这一位置信息，还需要格子位置，所以需要得到这个矩阵的行列数

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board) #行数
        n = len(board[0]) # 列数

        #定义dfs，传参要找的字符下标K和矩阵位置i,j
        def dfs(k,i,j):
            # 行列数越界或格子元素不等于字符串的情况下，返回
            if i<0 or i>=m or j>=n or j<0 or board[i][j]!=word[k]:
                return False
            # 如果格子元素等于字符串元素，先判断是否是字符串最后一个元素，是直接返回
            if k == len(word)-1:
                return True
            # 否，需遍历格子的上下左右是否含有下一步要找的字符
            # 由于不允许重复访问，所以记录当前访问结点并修改成一个不可能访问的值，这里我修改成！
            temp = board[i][j]
            board[i][j] = '！'
            res = dfs(k+1,i-1,j) or dfs(k+1,i+1,j) or dfs(k+1,i,j-1) or dfs(k+1,i,j+1) #上下左右
            board[i][j]= temp #最后再把元素归位，因为从任意点出发，一次遍历不行还需要从另一个点出发遍历，需要保持完整性
            return res
        # 从任意位置出发
        for i in range(m):
            for j in range(n):
                if dfs(0,i,j): # 如果能找到一个元素存在，返回true
                    return True
        return False
            

剑指offer13：机器人的运动范围

这一题跟上一题类似，也采用回溯，只是从判断格子里的值变成判断坐标和和k的关系。并且已经给出了行列数.而且是从左上角出发的，就变成只需要走右边的路或下边的路就可以了。
此外，还需要考虑求数位和的问题，怎么求数位和？

class Solution:
    def movingCount(self, m: int, n: int, k: int) -> int:
        #求数位和
        def digitsum(i,j):
            res =0
            # 求横坐标数位和
            while i:
                a = i%10
                res+=a
                i = i//10
            #求纵坐标数位和
            while j:
                b = j%10
                res+=b
                j = j//10
            return res
        # dfs,定义一个访问数组，只访问一次，初始为空，每遇到一个就放进去
        visited = set()
        def dfs(i,j):
        #如果越界，或者数位和大于K，或者格子已经被访问，就返回
            if i<0 or i>=m or j<0 or j>=n or digitsum(i,j)>k or (i,j) in visited:
                return False
            #如果格子没有访问过，标记为已访问（也就是加进访问集合中）
            visited.add((i,j))
            # 求格子数要包括它本身所以还要加1
            result =1+dfs(i+1,j)+dfs(i,j+1)
            return result

        return dfs(0,0)
            

总结：本题要写两个地方的代码，一个是求数位和，数位和要求横坐标和列坐标的数位和
一个是DFS遍历格子，并且标记访问。

剑指offer14-1：剪绳子

假设绳子的长度为n，最少剪1刀，最多剪N刀，那么有n-1种剪法：

假设剪一次剪的长度为i，每剪一次，剩下的绳子长度为n-i。每剪一次，都面临一次选择：剪还是不剪。不剪的话剩余长度为n-i，剪的话剩余长度为f(n-i)，要求最大乘积，所以要有一个max比较两种选择哪个更长：max[n-i,i×f(n-i)]。
而总的递推公式为：f(n) = max[f(n),i×max[n-j,f(n-i)]]。所以这是一道动态规划题，递推公式是转移方程。

class Solution:
    def cuttingRope(self, n: int) -> int:
        dp = [0]*(n+1) # 题目中返回的是k[]之间的乘积，所以初始化一个这种形式
        for i in range(2,n+1): #从第二次剪开始，可以剪2到n次
            for j in range(1,i): #每次剪长度为j的绳子，j的取值范围从1到绳子长度，由于每次剪绳子长度都不少于1，所以i每增加一次至少绳子长度会增加1
                dp[i] = max(dp[i],j*max(dp[i-j],i-j))
        return dp[n]

剑指offer15：二进制中1的个数

如果一个整数不为0，那么这个整数至少有一位是1。如果我们把这个整数减1，那么原来处在整数最右边的1就会变为0，如果最右边的1后面还有0的话，原来在1后面的所有的0都会变成1。其余前面的所有位将不会受到影响。

class Solution:
    def hammingWeight(self, n: int) -> int:
        # count 统计与运算的次数
        count = 0
        # 直至N是0，只要N不是0，就一定还有1，就要-1做与然后消1
        while n:
            n = n&(n-1)
            count+=1
        return count

剑指offer16：数值的整数次方

传统的幂运算，是对底数进行连乘，时间复杂度为o(n)，例如：2^13 = 2*2……*2，连乘十三次。所以引入快速幂的概念，先把指数表示成二进制形式，利用指数的二进制，可以实现复杂度为o(logn)的幂运算。13的二进制为1101，因此2的13次方可以分解成以下形式：

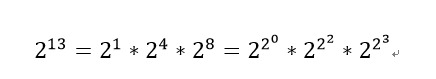
class Solution:
    def myPow(self, x: float, n: int) -> float:
        if x == 0:
            return 0
        if n <0:
            x = 1/x
            n = -n
        res = 1
        while n:
            if n& 1:
                res = res * x
            x = x * x
            n>>=1
        return res 

剑指offer18：删除链表中的节点

class Solution:
    def deleteNode(self, head: ListNode, val: int) -> ListNode:
         p =ListNode(-1)
         p.next=head
         pre = p
         while pre.next:
             if pre.next.val == val:
                 pre.next = pre.next.next
                 break
             pre = pre.next
         return p.next

剑指offer21：调整数组顺序使奇数位于偶数前面

一开始的思路是挨个遍历，遇到偶数就放到偶数组，遇到奇数就放到奇数组，如何再合并两个数组，但是复杂度高。考虑用双指针，左边找需要放到后面的，右边找需要放到前面的。这个题目需要放到前面的是奇数，放到后面的是偶数，所以左指针找需要放到后面的偶数，右指针找需要放到前面的奇数，找到后两个一交换，如何再分别指向下一个和前一个，继续找。

class Solution:
    def exchange(self, nums: List[int]) -> List[int]:
        left = 0
        right = len(nums)-1
        # 遍历结束的条件为指针相遇
        while left<right:
            #左指针一直找，直到找到一个偶数
            while left<right and nums[left]&1 == 1:
                left+=1
            # 右指针一直找，直到找到一个奇数
            while left<right and nums[right]&1 == 0:
                right-=1
            # 左右指针元素交换
            nums[left],nums[right] = nums[right],nums[left]
            # 指向下一个
            left+=1
            right-=1
        return nums

剑指offer22：链表的倒数第k个节点

由于链表只能从头到尾查找，考虑快慢双指针，快的指针比慢的指针快k步，当快的指针先到链表尾部，慢指针指向倒数第k个节点。

class Solution:
    def getKthFromEnd(self, head: ListNode, k: int) -> ListNode:
        fast = head
        slow = head 
    
        # fast 先走K步
        for i in range(k):
            fast = fast.next
        # 一直走，直至fast指向空
        while fast:
            fast = fast.next
            slow = slow.next
        return slow

剑指offer24：翻转链表

链表的头插法

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
         new = ListNode()
         p = new
         q = head
         while q!=None:
             temp = q.next
             q.next = p.next
             p.next = q
             q = temp
         return new.next

剑指offer25：合并两个排序的链表

class Solution:
    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        new = ListNode()
        p = new
        while l1 and l2:
            if l1.val<= l2.val:
                p.next=l1
                l1 = l1.next
            else:
                p.next=l2
                l2=l2.next
            p = p.next
        p.next = l1 if l1 else l2
        return new.next

剑指offer26：树的子结构

看见树就考虑递归，使用递归就考虑跳出递归的终止条件,这个题目的终止条件是遇到其中一方为空树。

class Solution:
    def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
    # 递归函数，判断两棵树是不是完全一样
        def same(t1,t2):
            # T2对应B根节点
            if t2 is None:return True
            # T1对应A中子树根节点
            if t1 is None:return False
            # 如果从根开始就不一样就没必要再看了
            if t1.val != t2.val:
                return False
            # 如果根一样，再看左子树和右子树
            return same(t1.left,t2.left) and same(t1.right,t2.right)
        # 如果有一方是空树，错误，不需要进入递归
        if A is None or B is None:return False
        # 否则就进入递归从根开始判断
        if same(A,B):return True
        # 如果当前根不一样，就从左右子树中找子结构
        return self.isSubStructure(A.left,B) or self.isSubStructure(A.right,B)
            

剑指offer27：二叉树的镜像

递归交换二叉树的左右孩子，递归终止条件为根节点为空

class Solution:
    def mirrorTree(self, root: TreeNode) -> TreeNode:
        # 交换左右子树
        if root is None:
            return None
        else:
            root.left,root.right =root.right,root.left
        self.mirrorTree(root.left)
        self.mirrorTree(root.right)
        return root

剑指offer28：对称的二叉树

也是用了递归，判断左子树是不是等于右子树。
一开始理解为左右子树相等，其实不是，是左子树的左等于右子树的右，左子树的右边等于右子树的左才是对称。（对称的二叉树可以看作一棵树左右子树是镜像关系）所以需要一个递归函数传参左右子树的根，对比两个对称位置节点的关系。

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
    # 递归函数判断左右子树是否对称，t1表示左子树根，t2表示右子树根
        def mirror(t1,t2):
             # 当两棵树都为空，返回TRUE
            if t1 is None and t2 is None:return True
             # 一棵空，肯定不是对称，返回false
            if t1 is None or t2 is None:return False
            # 值不等，也不对称
            if t1.val != t2.val:
                return False
             # 根相等，判断子树的子树，对称是左等于右，右等于左
            return mirror(t1.left,t2.right) and mirror(t1.right,t2.left)
        # 从根节点的子树开始调用判断对称的函数
        return mirror(root.left,root.right) if root else True

剑指offer29：顺时针打印矩阵

走到右边尽头，再走到下面尽头，再走到左边尽头，再走上面；如果右边还有路，就再走到右边尽头，如果下面还有路，就再走到下面尽头，以此类推。重要的是如何界定分界线。设四个指针，分别指向第一行top，最后一行bottom，第一列left，最后一列right

需要四步循环，
第一步向右走，left到right ，每循环一次top加1，直至bottom
第二步向下走，top到bottom，每循环一次right减1，直至left
第三步向左走，right到left，每循环一次bottom-1，直至top
第四步向上走，bottom到top，每循环一次left+1，直至right

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if matrix ==[]:
            return []
        # 左指针
        left = 0
        #上
        top = 0
        # 右
        right = len(matrix[0])-1
        #下
        bottom = len(matrix)-1
        res=[]
        while True:
        #向右
            for i in range(left,right+1):
                res.append(matrix[top][i])
            top+=1
            if top>bottom:break
              # 向下
            for i in range(top,bottom+1):
                res.append(matrix[i][right])
            right-=1
            if right<left:break
              # 向左
            for i in range(right,left-1,-1):
                res.append(matrix[bottom][i])
            bottom-=1
            if bottom<top:break
              # 向上
            for i in range(bottom,top-1,-1):
                res.append(matrix[i][left])
            left+=1
            if left>right:break
        return res
            

剑指offer31：栈的压入、弹出序列

定义一个栈来模拟压入弹出操作，每压入一个就判断栈顶是不是要弹出的元素，如果是，就弹出，并且指向下一个弹出元素，如果不是，就继续压入，直至找到那个元素或找不到那个元素。所以需要一个栈，一个弹出序列的索引popindex

class Solution:
    def validateStackSequences(self, pushed: List[int], popped: List[int]) -> bool:
    # 定义一个空栈
        stack=[]
        # 弹出序列的索引
        popindex = 0
        # 将压栈序列挨个压入
        for i in range (len(pushed)):
            stack.append(pushed[i])
            # 每压入一个就判断栈顶元素是不是弹出元素或者栈是否已空
            while stack and stack[-1] == popped[popindex]:
                stack.pop(-1) #弹出
                popindex+=1 #指向下一个要弹出的元素
        return not stack
            

剑指offer32-1：从上到下打印二叉树

二叉树的层次遍历，借用BFS思想，使用队列。从根节点开始，每遍历到一个节点就加入队列中，如何根据队首元素的左右孩子，加入队尾，弹出队首，只要队列中元素不为空，就依次根据队首元素把其左右孩子加入队尾并删除队首元素，直至队列为空。

class Solution:
    def levelOrder(self, root: TreeNode) -> List[int]:
        if root is None:
            return []
        res =[]
        queue = collections.deque()
        queue.append(root)
        while queue:
            node = queue.popleft()
            res.append(node.val)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        return res

剑指offer32-2：从上到下按层打印二叉树

根上一题类似，也需要一个队列实现，不同的是输出的是一个每层的结果，重点在怎么区分层与层。上一题我们每弹出一个队首元素，就把下一层的孩子加进队列，所以在队列里加孩子之前，先弹出队列中的所有元素加入结果集，就是一层的结果。

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []
        res =[]
        queue = collections.deque()
        queue.append(root)
        while queue:
            layer_res = []
            for i in range(len(queue)):
                node = queue.popleft()
                layer_res.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            res.append(layer_res)
        return res

剑指offer32-3：从上到下按之字打印二叉树

利用双端队列deque的数据结构，正常的顺序是按队首弹出元素，但是双端队列也可以按队尾弹出元素，这个题目要求偶数行从队尾弹出，奇数行从队首弹出就能实现了。那么问题是怎么区分奇数行和偶数行，上一个题目中，while循环的就是每一行，那么在while中写两个同级的循环，第一个就是奇数行的，第二个就是偶数行的。

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if root is None:
            return []
        queue = collections.deque()
        res = []
        queue.append(root)
        while queue:
            # 奇数
            layer_res=[]
            for i in range(len(queue)):
                node = queue.popleft()
                layer_res.append(node.val)
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            res.append(layer_res)
            # 偶数
            if not queue:break

            layer_res=[]
            for i in range(len(queue)):
                # 偶数行的区别，从队尾弹出，用pop
                node = queue.pop()
                layer_res.append(node.val)
                # 偶数行的区别，入队的时候先右孩子后左孩子，用appendleft,否则乱序
                if node.right:
                    queue.appendleft(node.right)
                if node.left:
                    queue.appendleft(node.left)
            res.append(layer_res)
        return res

剑指offer33：二叉搜索树的后序遍历序列

这个题目要判断一个序列是不是二叉搜索树的后续遍历。所以需要明确二叉搜索树的性质和后序遍历。二叉搜索树的左孩子小于根，右孩子大于根，而后序遍历是左右根的顺序。

按照题目中给的这棵树，它的后序遍历是[1,3,2,6,5]对应到左右子树和根节点就是[1,3,2][6][5]。观察可以发现，一棵二叉搜索树的后序遍历，根是后序遍历的最后一个数，左子树的数比根小，右子树的数都比根大。

那么每次取序列的最后一个元素last，从头往后遍历，遇到比last小的，就说明还在左子树序列中，继续往后找，直到找到一个比他大的，此时记为right，然后从right开始找是不是都比last大，是的话就左子树序列和右子树序列和根就满足，然后再对左右子树序列进行检查，左右子树是否也符合二叉搜索树的后序遍历规律，所以这个题目需要用到递归。

class Solution:
    def verifyPostorder(self, postorder: List[int]) -> bool:
        # 递归函数，i是序列开始，last是序列结束
        def judge(i,last):
            if i>=last:
                return True
            # 找比last小的
            index = i
            while postorder[index]<postorder[last]:
                index = index+1
            # 找比last大的
            right = index
            while postorder[index]>postorder[last]:
                index = index+1
             # 如果右序列都比last大，此时index应该等于last，否则就不成立
             # 再递归检查左右子树，注意右子树要减去last位置的元素
            return index==last and judge(i,right-1) and judge(right,last-1)
        # 在主函数中调用递归函数
        return judge(0,len(postorder)-1)

剑指offer34：二叉树中和为某一数的路径

首先要明确一点，找路径是从根节点找到叶节点，所以要从上往下走，另外，路径可能不止有一条，所以需要一个结果集来保存所有可能的结果。

那么怎么找呢？最简单的方法就是从节点root开始，先把这个节点加入路径path中，然后计算加入后的target还差多少（也就是target-root.val==?），如果此时target减去一个值后刚好为0而且这个节点也没有左右孩子是个叶节点，那么path中就找到了一条路径，把path加入结果集。如果不满足target=0或者不是叶节点，就继续找左右子树。最后输出结果集res.

class Solution:
    def pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:
        # 结果集
        res = []
        # 记录路径
        path = []
        def find(root,target):
            if root is None:
                return
            # 遇到一个节点先加进路径，后判断是否需要弹出
            path.append(root.val)
            # 怎么判断呢，就是判断target和叶节点
            target= target-root.val
            if target==0 and root.left is None and root.right is None:
                res.append(path[:]) # 找到了一条路径，加入结果集
            find(root.left,target)  # 不满足要求，找左右孩子
            find(root.right,target)
            path.pop()             # 弹出，相当于回溯
        # 在主函数中调用递归函数
        find(root,sum)
        return res