数据结构经典算法（待完善）_用30秒讲授数据结构中编写最优算法-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_41744192/article/details/119768747

本文深入探讨了三种经典的排序算法——快速排序、归并排序和堆排序，通过伪代码和图解详细阐述了它们的工作原理。此外，还介绍了01背包问题和完全背包问题的动态规划解决方案，展示了如何利用回溯法解决组合问题。文章结合实例代码，帮助读者理解这些基础但重要的算法思想。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

数据结构经典算法

排序小总结
- 快排&归并排
- 堆排序
链表问题
背包问题
回溯法
数学
- - - sqrt
    - pow
概率
动态规划
数组
树

排序小总结

快排&归并排

把这两个放在一起写是因为在这两种排序在结构上有类似的操作，但是又都有他们特殊的地方。
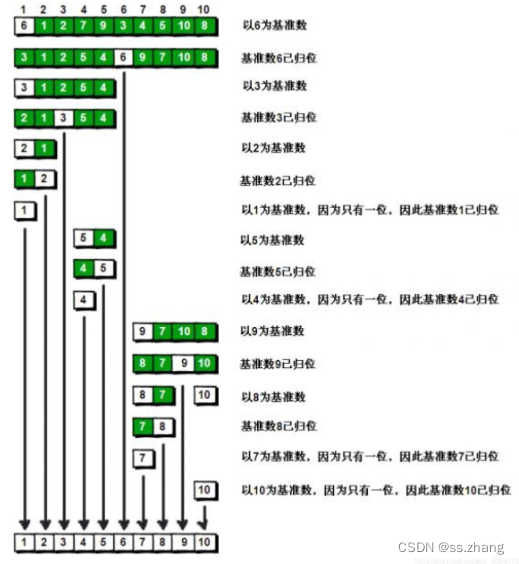
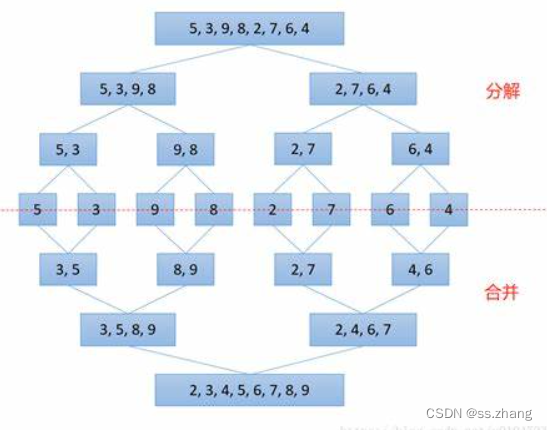
快速排序的思想可以用一句话总结，确定一个基准点的位置，然后左右分为两个序列，继续确定下一个基准点的位置。这个递归过程可以理解为二叉树的先序遍历结构。归并排序的过程为先将序列不断二分，然后在递归返回的过程中排序整合序列，这个过程可以理解为二叉树的后序遍历过程。
伪代码如下

#快速排序
def dfs(start,end):
	#确定基准点位置在mid上
	dfs(start,mid-1)#对左边的序列重复操作
	dfs(mid+1,end)#对右边的序列重复操作
	return
#归并排序
def dfs(start,end):
	dfs(start,mid-1)#对左边的序列重复操作
	dfs(mid+1,end)#对右边的序列重复操作
	#排序并合并左右两个序列
	merger(start,end)
	return

快速排序图解
在这里插入图片描述
完整代码

# 等价于二叉树的前序遍历，
    def quicksort(self,num):
        def dfs(l,r):
            if l>=r:return #递归结束条件：左右指针重逢
            start,end,mid = l,r,l #位置初始化，每次初始化最左边的点为mid点
            while(l<r):# 双指针
                while num[mid] <= num[r] and l < r:r -= 1#在mid右边找到小于mid的点
                num[mid],num[r] = num[r],num[mid]#r和mid交换数值
                mid = r#更新mid指针
                while num[l] <= num[mid] and l < r:l += 1#在mid左边找到大于mid的点
                num[mid], num[l] = num[l], num[mid]#r和mid交换数值
                mid = l#更新mid指针，结束一次while操作后mid左边都小于mid，右边都带mid
            dfs(start,mid-1)#对左边的序列重复操作
            dfs(mid+1,end)#对右边的序列重复操作
            return
        dfs(0,len(num)-1)
        return

归并排序图解
在这里插入图片描述
归并排序完整代码

    def mersort(self,num):
	    def merge_num(l,mid,r):
	            m_num, num_l, num_r= [], num[l:mid+1], num[mid+1:r+1]
	            while len(num_l)!=0 and len(num_r)!=0:
	                m_num += [num_l.pop(0)] if num_l[0] < num_r[0] else [num_r.pop(0)]
	            m_num += num_l if len(num_l)!=0 else num_r
	            return m_num
        def dfs(l,r):
            if l == r:return#递归终止条件：分裂到一个点
            mid = (l + r)//2#获取当前序列的中点
            dfs(l,mid)#左边继续分
            dfs(mid+1,r)#右边
            num[l:r+1] = merge_num(l,mid,r)#排序合并
        dfs(0,len(num)-1)
        return

堆排序

堆排序的思路可以分为2步：
将序列数组按层次构建一颗二叉树
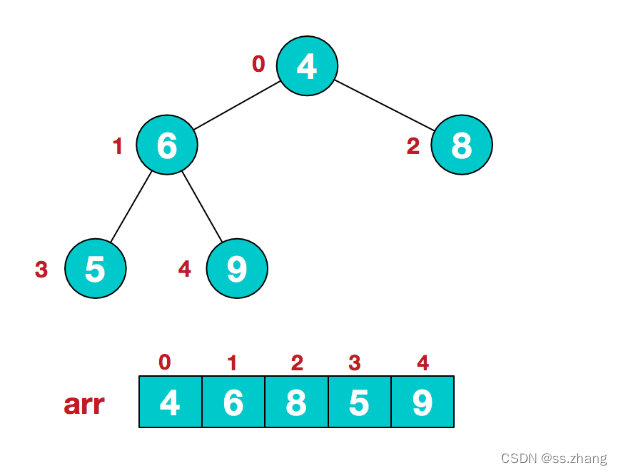
在这里插入图片描述

调整二叉树为大顶堆
输出顶点，重新调节二叉树，重复此过程

    def heap_sort(self,num):
        # 1. 生成标准大顶堆，从最后一个非叶结点(len(num)//2-1)，往上逐个调整
        for i in range(len(num)//2-1,-1,-1):
            buid_tree(i,len(num)-1)
        # 2. 输出大顶，并调整大顶堆，从最小的叶子结点和根节点进行交换
        for i in range(len(num)-1,0,-1):
            num[i], num[0] = num[0], num[i] #头尾交换
            buid_tree(0,i-1)
                # 调整结点0为大顶堆i-1保证最后的元素已经固定不再改变
        def buid_tree(start,end):
            j = start * 2 + 1#获取当前结点i的左子树
            while j <= end:# 越界判断
                # 获取较大的一个子节点:如果右节点存在且右节点大于左节点，切换到右节点
                if j+1 <= end and num[j+1] > num[j]:j += 1 #小顶堆调整符号即可
                if num[j] > num[start]:#和根节点比较,大于就交换，小顶堆调整符号即可
                    num[start], num[j]= num[j], num[start]
                    start, j = j, j*2+1 #交换后可能导致交换后的结点子树不满足条件，需要检查调整
                else:break# 子树都没有根节点大 不需要调整，直接结束
            return
        print(num)
        return num

链表问题

背包问题

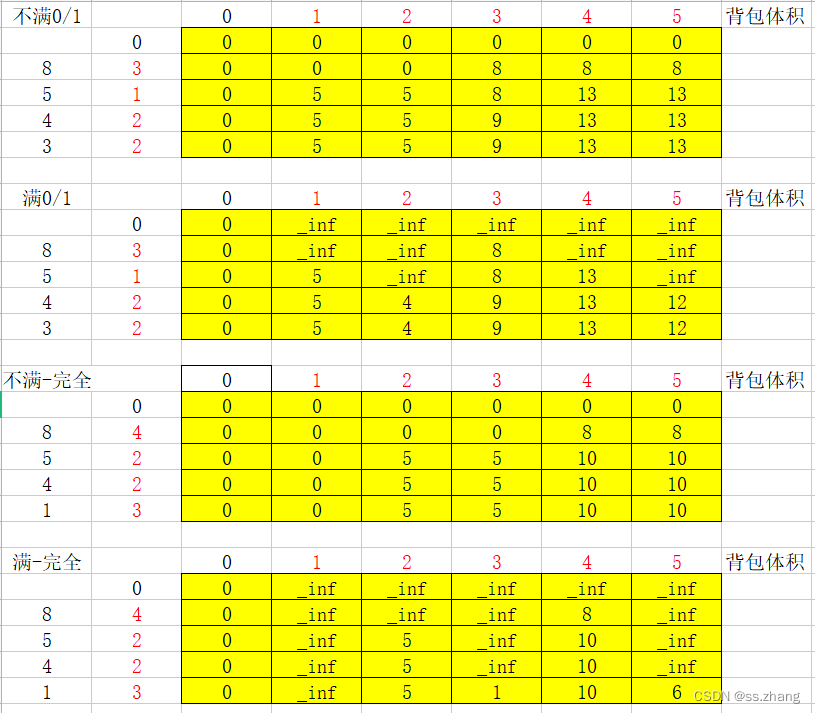
01背包

class soultion():
    def o_i(self):
        v = 5  #背包容量
        wv = [3,1,2,2]# 体积
        wt = [8,5,4,3]# 价值
        # 背包不用装满,物品价值为0时，初始化为dp[0][0]为0，dp[0][1~v] = 0
   	    # 背包装满,物品价值为0时，初始化为dp[0][0]为0，dp[0][1~v] = -inf
        dp = [[0]*(v+1) for _ in range(len(wt)+1)]
        #for i in range(1,v+1):
        #	dp[0][i] = float('-inf')
        for i in range(1,len(wt)+1):#体积选择
            for j in range(1,v+1):#背包体积选择
                if j - wv[i-1] < 0:
                    #大于当前背包体积，装不了
                    dp[i][j] = dp[i-1][j]
                else:
                    # max（不装这个dp[i-1][j]，装这个dp[i-1][j-wv[i-1]]+wt[i-1]）
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-wv[i-1]]+wt[i-1])
        return dp[-1][-1]

完全背包

$完全背包的变化只有一点，那就是使用一个物品时，可以建立在之前使用过的基础上 i - 1 变为 i$

$d p [i] [j] = ma x (d p [i - 1] [j], d p [i - 1] [j - w v [i - 1]] + wt [i - 1])$

$d p [i] [j] = ma x (d p [i - 1] [j], d p [i] [j - w v [i - 1]] + wt [i - 1])$

class soultion1():
    def wq1(self):
        v = 5  # 背包容量
        wv = [4,2,2,3]# 体积
        wt = [8,5,4,1]# 价值
        # 背包不用装满,物品价值为0时，初始化为dp[0][0]为0，dp[0][1~v] = 0
        dp = [[0]*(v+1) for _ in range(len(wt)+1)]
   	    # 背包装满,物品价值为0时，初始化为dp[0][0]为0，dp[0][1~v] = -inf
        #for i in range(1,v+1):
        #	dp[0][i] = float('-inf')
        for i in range(1, len(wt) + 1):
            for j in range(1, v + 1):
                if j - wv[i - 1] < 0:
                    #大于当前背包体积，装不了
                    dp[i][j] = dp[i - 1][j]
                else:
                    # 不装这个 dp[i-1][j]
                    # 装这个，可以重复使用当前物品体积选择dp[i][j-wv[i-1]]+wt[i-1]）
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - wv[i - 1]] + wt[i - 1])
        #print(dp)
        return dp[-1][-1]

图解

在这里插入图片描述

回溯法

遍历问题，控制二维数组的索引进行上下左右进行回溯，不同题目的遍历条件不同，例如岛屿问题不走0，机器人寻路和小于target等
排列问题，又分为重复排列，不重复排列
组合问题，由排列演变而来，排列的终止条件为len(track)==len(nums)，组合可以为其他条件例如何为target，数量为n等

数学

sqrt

pow

概率

给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数，试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。

# 第一种情况随机的范围小于目标范围 先使用二分的思路将 目标rand10拆分为小于当前的rand7，的1-5和6-10，然后就可以使用第一次的rand7选定区间，使用第二次的rand7进行舍弃性随机1-5 或者 6-10
# 第二种大于的情况，比较容易，可以使用如果差距不大可以使用舍弃性随机，较大的可以使用区间来对应随即目标
# 例如rand10 -> rand4 1-5表示1-2，6-10表示3-4，以此类推
class Solution(object):
    def rand10(self):
        f = rand7()
        while f == 4:
            f = rand7()
        o = rand7()
        while o > 5:
            o = rand7()
        return o if f < 4 else o + 5
        
# The rand7() API is already defined for you.
# def rand7():
# @return a random integer in the range 1 to 7

class Solution(object):
    def rand10(self):
        def get_random10():
            f = rand7()#1代表1-7区间，2代表8-14，....7代表43-49
            o = rand7()#1代表取当前区间第2个数，1代表取当前区间第2个数....
            qu_jian = [f*7-6,f*7]
            out = qu_jian[0] + o - 1
            return out
        while 1:
            out = get_random10()
            if out < 11:
                return out