初刷leetCode--数组系列--Pascal's Triangle&Pascal's Triangle II(杨辉三角)

最新推荐文章于 2022-02-08 09:03:48 发布

六月的雨听海

最新推荐文章于 2022-02-08 09:03:48 发布

阅读量210

点赞数 1

CC 4.0 BY-SA版权

分类专栏： leetCode系列文章标签： leetCode 刷题杨辉三角数组

本文链接：https://blog.youkuaiyun.com/weixin_41726080/article/details/88412938

leetCode系列专栏收录该内容

3 篇文章

订阅专栏

本文深入探讨了杨辉三角的算法实现，包括其状态方程及代码实现。从杨辉三角的基本概念出发，详细解释了如何通过递推公式计算每一层的值，并提供了两种不同的算法实现方式，一种是生成整个杨辉三角，另一种是在O(k)空间复杂度下直接求得第k层的结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

接着上一章节的Maximum Subarray（最大连续子序列）的问题，继续筛选题目，中间跳过了几道题目

Plus One:需要注意最后一位为9与全为9的情况；
Merge Sorted Array：则是插入排序的问题，不了解的人请去翻阅数据结构；

接下来的连续两道杨辉三角的题目挺有趣，作为本文的重点。
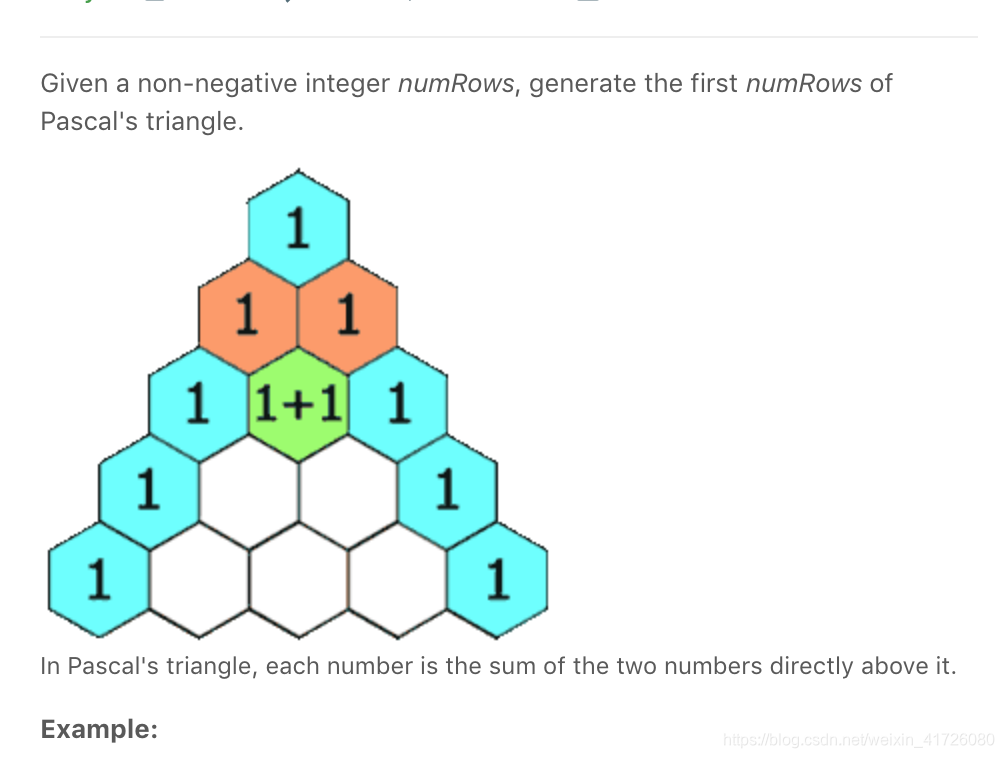
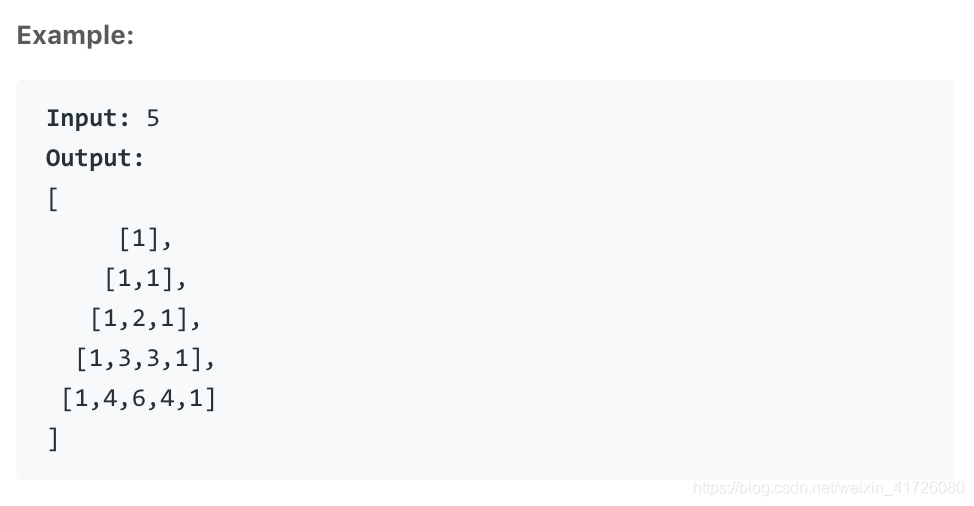
图片来自于leetCode 图片来自leetCode
这是杨辉三角第一题，这里在计算第k层的数组时，有个状态方程，首先定义初始状态

解题思路

k=1, PT[1][0] = 1;
k=2时, PT[1][0/1]=1,;
通过上边可知，当k>2时，每一层首尾都为1， PT[k][0]=1, PT[k][i]=PT[k-1][i-1]+PT[k-1][i]
对应的代码实现如下：

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> pts;
        pts.resize(numRows);
        
        for(int i = 0; i < numRows; i++){
            pts[i].resize(i+1);
            pts[i][0] = 1;
            pts[i][pts[i].size()-1] = 1;
            for(int j = 1; j < pts[i].size()-1; j++){
                pts[i][j] = pts[i-1][j-1]+pts[i-1][j];
            }
        }
        return pts;
    }
};

杨辉三角 II 问题描述

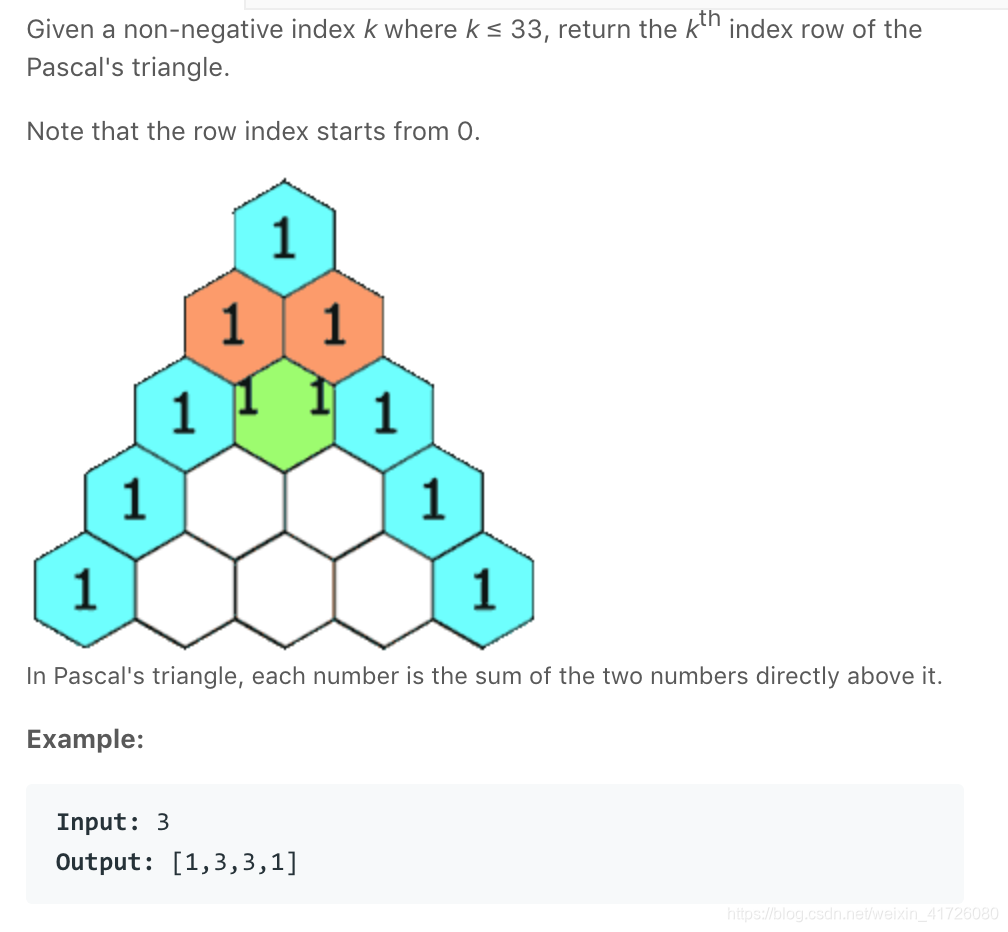
问题来着leetcode

问题分析

这道题是上道题的变种，求第k层的结果。最简单的方法是，求出每一层，然后输出第k层的结果。但是这样不满足题目的空间复杂度是O(k)的要求。

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex + 1);
        res[0] = 1;
        for(int i = 1; i <= rowIndex; i++)
             for(int j = i; j >= 0; j--)
                 if (j == i)
                     res[j] = res[j-1];
                 else if (j == 0)
                     res[j] = res[j];
                 else
                     res[j] = res[j-1] + res[j];
         return res; 
    }
};