House Prices top5% 关于代码的一些笔记_github houseprice-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_41684423/article/details/115613157

思路来源&致谢：https://www.kaggle.com/jesucristo/1-house-prices-solution-top-1?scriptVersionId=12846740

git 地址： https://github.com/jamjar102/kaggle_HousePrice new.py文件跑出来的submission score大概0.11 达到top5%

具体思路可以看kaggle的这篇教程和我代码上的一些注释，以下大概写几个之前没有用过的技术点。

记性不好，写下来自己看防止以后忘记。

一、数据分析

1.标签分布：

sns.distplot(y, kde=False, fit=stats.johnsonsu)
sns.distplot(y, kde=False, fit=stats.norm)
sns.distplot(y, kde=False, fit=stats.lognorm)

其中y为标签序列，采用不同的fit函数可以用不同的分布去进行拟合。

2.stats.shapiro（）

    test_normality = lambda x: stats.shapiro(x.fillna(0))[1] < 0.01 #统计学知识

输出结果中第一个为统计量，第二个为P值（统计量越接近1越表明数据和正态分布拟合的好，P值大于指定的显著性水平，接受原假设，认为样本来自服从正态分布的总体）

以下来自scipy官网：

The Shapiro-Wilk test tests the null hypothesis that the data was drawn from a normal distribution.

该检测的无效假设是该分布符合正态分布。对于N>5000的样本可能会造成p值不准确

以下致谢这篇优快云文章：https://blog.youkuaiyun.com/weixin_42059534/article/details/101703027

'''输出结果中第一个为统计量，第二个为P值（统计量越接近1越表明数据和正态分布拟合的好，
P值大于指定的显著性水平，接受原假设，认为样本来自服从正态分布的总体）''' 相当于P值越小越拒绝原假设（拒绝无效假设）
print(stats.shapiro(a))

kstest的原假设是两个分布相同，所以p值大于阈值可以接收
'''输出结果中第一个为统计量，第二个为P值（注：统计量越接近0就越表明数据和标准正态分布拟合的越好，
如果P值大于显著性水平，通常是0.05，接受原假设，则判断样本的总体服从正态分布）'''
print(stats.kstest(a, 'norm'))

'''输出结果中第一个为统计量，第二个为P值（注：p值大于显著性水平0.05，认为样本数据符合正态分布）'''
print(stats.normaltest(a))

为什么p值越小约拒绝原假设：https://www.zhihu.com/question/35891708

个人理解：

相当于认为此分布为正态分布，正态分布有对应的各种情况出现的概率，然后去进行抽取实验或者什么实验去验证，但是抽出来的结果是十分极端的（在原假设下概率出现的十分低），概率低，p值低，所以拒绝原假设，即不认为当前数据的分布为正态分布。

3. 对离散型变量进行encode

    def encode(frame, feature):
        ordering = pd.DataFrame()
        ordering['val'] = frame[feature].unique()  #数组返回该特征里面属性的唯一值（去重）
        ordering.index = ordering.val
        ordering['spmean'] = frame[[feature, 'SalePrice']].groupby(feature).mean()['SalePrice']
        ordering = ordering.sort_values('spmean')
        ordering['ordering'] = range(1, ordering.shape[0] + 1)
        ordering = ordering['ordering'].to_dict()

        for cat, o in ordering.items():
            frame.loc[frame[feature] == cat, feature + '_E'] = o
            #print(frame)


    qual_encoded = []
    for q in qualitative:   #离散型特征名
        encode(train, q)
        qual_encoded.append(q + '_E')
    print(qual_encoded)  #处理后的数值特征名 + _E

其中 frame.loc[frame[feature] == cat, feature + '_E'] = o

参考官网教程：https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.loc.html

4.查看每列feature对标签的斯皮尔曼相关系数

    def spearman(frame, features):
        spr = pd.DataFrame()
        spr['feature'] = features
        spr['spearman'] = [frame[f].corr(frame['SalePrice'], 'spearman') for f in features]
        #这块调用的是https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.corr.html
        #series中的corr方法，第一个参数接收一个series参数

        spr = spr.sort_values('spearman') #排序
        #plt.figure(figsize=(6, 0.25 * len(features)))
        #sns.barplot(data=spr, y='feature', x='spearman', orient='h')
        #plt.show()


    features = quantitative + qual_encoded
    spearman(train, features)

其中：

spr['spearman'] = [frame[f].corr(frame['SalePrice'], 'spearman') for f in features]
#这块调用的是https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.Series.corr.html
#series中的corr方法，第一个参数接收一个series参数

5.查看特征相关系数，发现之前对特征进行encode之后可以直线增加相关性

# 查看相关稀疏矩阵
    corr = train[qual_encoded + ['SalePrice']].corr()
    sns.heatmap(corr)
    #plt.show()

    corr = train[quantitative + ['SalePrice']].corr()
    sns.heatmap(corr)
    #plt.show()

    corr = pd.DataFrame(np.zeros([len(quantitative) + 1, len(qual_encoded) + 1]), index=quantitative + ['SalePrice'],
                        columns=qual_encoded + ['SalePrice'])
    for q1 in quantitative + ['SalePrice']:
        for q2 in qual_encoded + ['SalePrice']:
            corr.loc[q1, q2] = train[q1].corr(train[q2])
    sns.heatmap(corr)

直接使用以下两行代码即可查看dataframe的相关性

corr = train[qual_encoded + ['SalePrice']].corr()
sns.heatmap(corr)

6. TSNE（）特征降维

致谢：https://www.cnblogs.com/bonelee/p/7849867.html

假设数据是均匀采样于一个高维欧氏空间中的低维流形，流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据的内在规律。

简单地理解，流形学习方法可以用来对高维数据降维，如果将维度降到2维或3维，我们就能将原始数据可视化，从而对数据的分布有直观的了解，发现一些可能存在的规律

model = TSNE(n_components=2, random_state=0, perplexity=50)

_components，int, default=2，means：Dimension of the embedded space.

对原始特征进行降维，备用。对原始特征进行标准化后进行PCA，PCA后进行聚类，按类别查看降维后（此处是2维）后的相关性

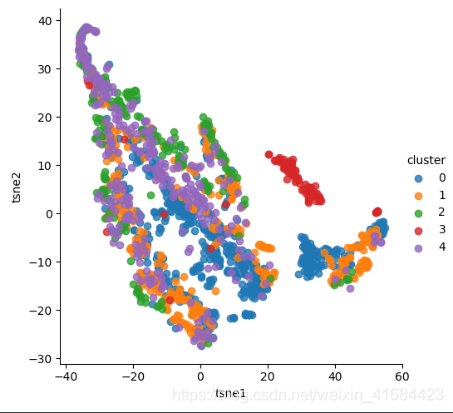
超级todo：进行了这些特征分析后对算法有什么帮助与提升呢？

二.数据处理

1.利用log1p和exp1p对数据进行平滑和恢复

train["SalePrice"] = np.log1p(train["SalePrice"])  #数据平滑处理

2.数据清洗后需要重新排序，X和y都要排序

y = train['SalePrice'].reset_index(drop=True)

3.dataframe.groupby

features['MSZoning'] = features.groupby('MSSubClass')['MSZoning'].transform(lambda x: x.fillna(x.mode()[0]))

致谢：https://www.cnblogs.com/bjwu/p/8970818.html

4.dataframe.update()

5.去掉0太多的特征列

    #0太多的去掉
    overfit = []
    for i in X.columns:
        counts = X[i].value_counts()
        zeros = counts.iloc[0]
        if zeros / len(X) * 100 > 99.94:
            overfit.append(i)

    overfit = list(overfit)
    X = X.drop(overfit, axis=1)
    X_sub = X_sub.drop(overfit, axis=1)

三、Model

大体：参见代码

1.RobustScaler()

致谢：

https://blog.youkuaiyun.com/u013749051/article/details/105870716

2.几个用到的回归&之间的关系：

线性回归的目的是要得到输出向量Y和输入特征X之间的线性关系,求出线性回归系数θ，也就是Y=Xθ, 其中Y的维度为m x 1,X的维度为 m x n，而θ的维度为 n x 1, m代表样本个数, n代表样本特征的维度

RidgeCV（岭回归）：只要数据线性相关，用LinearRegression拟合的不是很好，需要正则化，可以考虑使用RidgeCV回归, 如何输入特征的维度很高,而且是稀疏线性关系的话， RidgeCV就不太合适,考虑使用Lasso回归类家族

LassoCV：Lasso回归可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0，从而增强模型的泛化能力
使用场景:对于高纬的特征数据,尤其是线性关系是稀疏的，就采用Lasso回归,或者是要在一堆特征里面找出主要的特征，那么 Lasso回归更是首选了

致谢：https://www.jianshu.com/p/88cb43166bae

3.regressor.StackingCVRegressor

StackingCVRegressor扩展了使用Stacking预测的标准Stacking算法（实现为StackingRegressor），预测的结果作为2级分类器的输入数据。
在标准 stacking程序中，拟合一级回归器的时候，我们如果使用第二级回归器的输入的相同训练集，这很可能会导致过度拟合。然而，StackingCVRegressor使用了‘非折叠预测’的概念：数据集被分成k个折叠，并且在k个连续的循环中，使用k-1折叠来拟合第一级回归器(即k折交叉验证的stackingRegressor)。
在每一轮中（一共K轮），一级回归器然后被应用于在每次迭代中还未用过的模型拟合的剩余1个子集。
然后将得到的预测叠加起来并作为输入数据提供给二级回归器。在StackingCVRegressor的训练完之后，一级回归器拟合整个数据集以获得最佳预测。