FCN表层理论学习 - 泰迪杯

FCN与CNN的异同

FCN与CNN在最后两层的选择有所差异，CNN最后阶段是全连接层，而FCN将最后的全连接层转换成了(n/32)*(n/32)*n的卷积层，虽然本质上好像没什么区别，但是FCN并不是利用这2个卷积层直接得出分类结果，而是将其当作一个特征图 (feature map) 对其进行上采样，使之大小与原图片相同，这样子可以得到每个像素点的预测值，实现在像素点层面对图像进行语义级别的识别与分割。

问题一：为什么要对最后阶段的全连接层替换为卷积层？

这里我们要引入一个图像目标检测的一个机制——卷积的滑动窗口机制
在使用卷积神经网络进行目标识别的时候经常使用滑动窗口机制，而这个滑动的窗口就是我们的滤波器（卷积核）。通过滤波器检测该窗口内是否有目标物体。那我们可以联想到卷积过程其实也是一个滑动窗口机制（通过滤波器得到output图像），而我们output图像每一个像素不正是滤波器对输入图像每一个预选框（Anchor Boxes）的输出结果么？

—————————————分割线——————————————

PS：关于Anchor Boxes的视频介绍

吴恩达老师的微专业中也有详细的介绍微专业入口何为Anchor Boxes。

—————————————分割线——————————————

因此在最后的阶段使用卷积层的目的也很明显——让卷积网络在一张更大的输入图片上滑动，得到多个输出，这样的转化只需一次卷积就可以完成，而不需要全连接算出来预测结果，比全连接层更便捷。而且可以看得出每一层都是前一层的预测。

问题二：如何利用上采样中的反卷积？

在FCN中使用的是反卷积对图像进行上采样，上采样在这里的语境就是将图像进行放大。那我们就来讨论一下他是如何放大图像的。这里参考知乎作者“那么”的反卷积输出尺寸计算公式，这篇文章非常通俗易懂，大家也可以去看看。
需要注意的是 反卷积是一种特殊的正向卷积，而不是卷积的反过程。
我们知道卷积的过程是将滤波器（卷积核）投影到input图像上将结果返回到output图像上。其公式为：
$$o=[(n+2p-k)/s+1].$$
上式需要向下取整！！
在给出反卷积计算公式前，我们来说明一下反卷积在图像像素中是如何放大图像的。

1. 对input图像进行stride变换，stride可以理解为在输入的相邻元素之间添加 s(步幅) - 1 个零元素，如何所示：
   
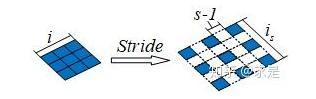
   可能在这里回有点不理解s到底指的是哪个步幅，这里指的是上方蓝色方块之间你自己想增加的方块数 加1。注意不要漏掉加1！！！！
   以上述变化后的结果进行原来的卷积操作便可以得到放大后的图片。
   最底下的为input图像，叠在上面的灰色为滤波器，最上面的是output图像。
   
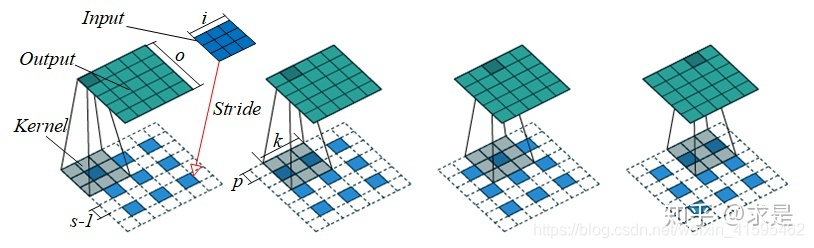
   反卷积的计算公式：
   首先对原本的input图像边长进行更新。
   $$i^{new}=i^{old}+(s-1)(i^{old}-1).$$
   然后带入卷积公式就可以得到：
   $$o=s(i-1)+2p-k+1$$