智能交通 | 邻接矩阵 | Dijkstra | 最优路径

最新推荐文章于 2022-06-21 01:26:50 发布

原创

最新推荐文章于 2022-06-21 01:26:50 发布 · 1.4k 阅读

5 ·

CC 4.0 BY-SA版权

本文探讨如何利用Dijkstra算法解决智能交通系统中的最佳路径选择问题。通过邻接矩阵作为存储结构，程序旨在找到从一个地点到另一个地点的最小花费路径。文章提到了在CodeBlocks中遇到的'`to_string`'未声明的问题，并提供了解决方案链接。

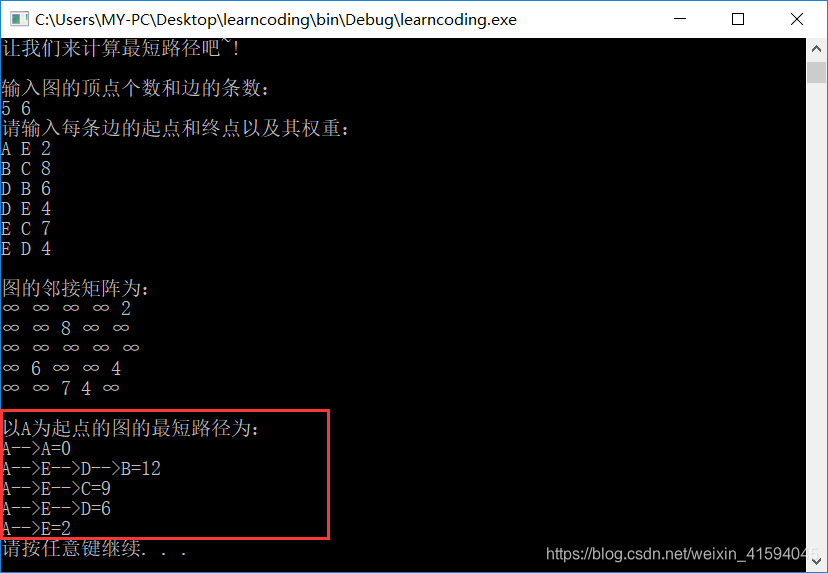
编写程序，实现智能交通中的最佳路径选择问题：设有n个地点，编号为0→n-1，m条路径的起点、终点和代价由用户输入提供，使用 [~~邻接表~~] 邻接矩阵为存储结构，寻找最佳路径方案（如花费时间最少，路径长度最短，交通费用最少等问题任选其一即可）

为什么用的是邻接矩阵？
没有为什么，看错题目了。。。。：）

codeblocks中报错：‘to_string’ was not declared in this scope解决方案：
https://blog.youkuaiyun.com/haofandedaima/article/details/90137837#commentBox

char转string

#include <sstream>
char c;
string str;
stringstream stream;
stream << c;
str = stream.str();

在这里插入图片描述

ITS.cpp [ Intelligent Transportation System ]

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include "Queue.h"
#include "Dijkstra.h"

using namespace std;

typedef struct eNode{
   
   
    char adjVex;     //任意顶点u相邻接的顶点
    int w;                  //边的权值
    struct eNode* nextArc;  //指向下一个边结点
}eNode;

typedef struct{
   
   
    int n;          //图的当前顶点数
    int e;          //图的当前边数
    eNode **a;      //指向一维指针数组
}lGraph;


int Init(lGraph *lg,int nSize){
   
           //初始化函数
    int i;
    lg->n = nSize;
    lg->e = 0;
    lg->a = (eNode **)malloc(sizeof(eNode*)*nSize);
    if(!lg->a){
   
   
        return 0;
    }
    else{
   
   
        for(i=0;i<nSize;i++){
   
   
            lg->a[i] = NULL;
        }
    }
    return 0;
}

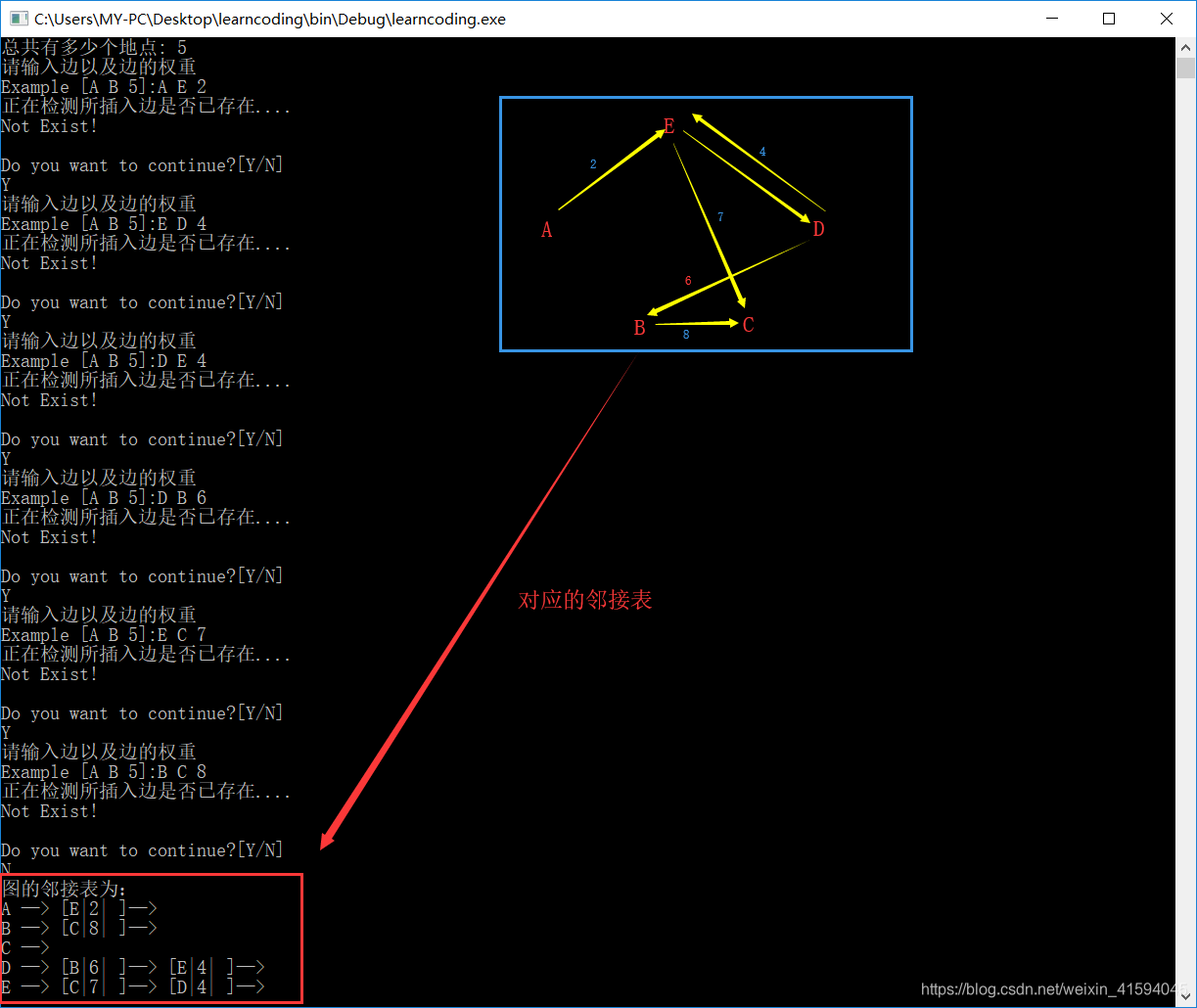
void Print(lGraph *lg){
   
                        //打印邻接表的函数
    int i=0;
    eNode *p;
    for(i=0;i<lg->n;i++){
   
   
        cout<<char(65+i)<<" —> ";
        p = lg->a[i];
        while(p){
   
   
            cout<<"["<<p->adjVex<<"|"<<p->w<<"| ]—> ";
            p = p->nextArc;
        }
        cout<<endl;
    }

}
int Exist(lGraph *lg,char u,char v){
   
         //检查边是否存在的函数
    eNode *p;
    if(int(u)<65||int(v)<65||int(u)>65 + lg->n-1||int(v)>65 + lg->n-1||u==v)
        return 0;
    p = lg->a[int(u)-65];
    while(p&&p