本文深入探讨了核函数的概念，强调它作为内积的等价表示所必需的条件。同时，阐述了原问题与对偶问题在优化中的角色，特别是当原问题是凸函数且约束为线性时的强对偶性。通过KKT条件，展示了原问题解与对偶问题解的关系，为求解复杂优化问题提供了理论基础。
一：关于核函数：
1 核函数是一个数
2 核函数必须满足一定条件，才能写成内积形式，条件如下：
二：关于原问题和对偶问题
原问题定义：
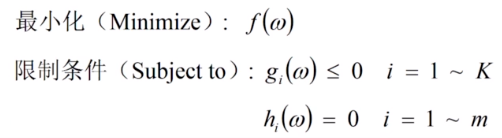
在以上定义中，自变量为w（多维向量），目标函数为f（w）。
其对应的对偶问题为：
根据以上定义，可以得到如下定理：
定理一：
证明如下：
定理二：强对偶定理
简单说，就是：如果原问题目标函数是凸函数，限制条件是线性函数，则原问题解等于对偶问题解。对偶差距为0.
根据定理一可以推导出KKT条件，具体如下：
扫一扫
评论
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
查看更多评论
添加红包
