机器学习—线性回归

最新推荐文章于 2024-08-21 10:57:28 发布

原创最新推荐文章于 2024-08-21 10:57:28 发布 · 177 阅读

0 ·

CC 4.0 BY-SA版权

机器学习专栏收录该内容

9 篇文章

订阅专栏

文章目录

线性回归

线性回归

大自然让我们回归到一定的区间范围之内；反过来说就是，有一个平均的水平，可以让突出的事物能向他靠拢

那些高个子的后代的身高，有种回归到大众身高的趋势
                                                --- 高尔顿

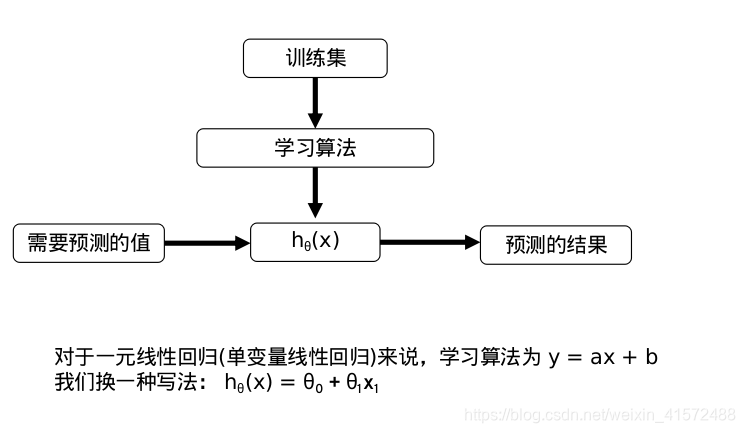
线性回归一般步骤

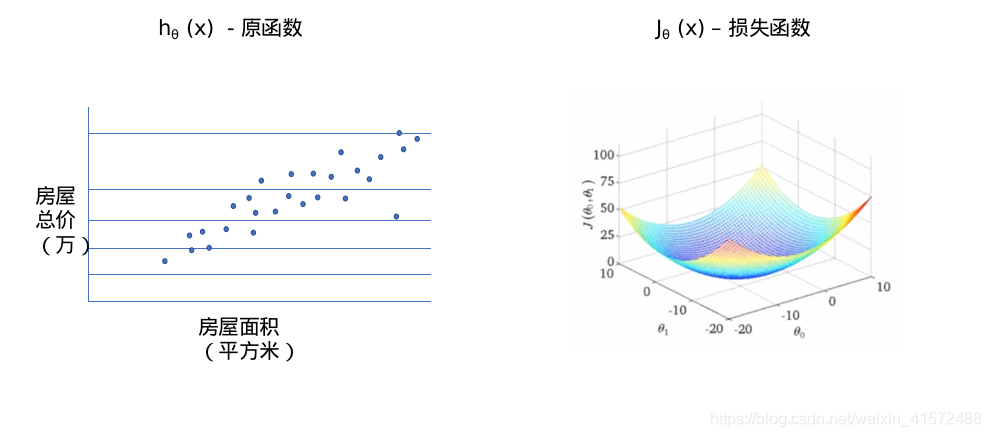
在这里插入图片描述

损失（代价）函数

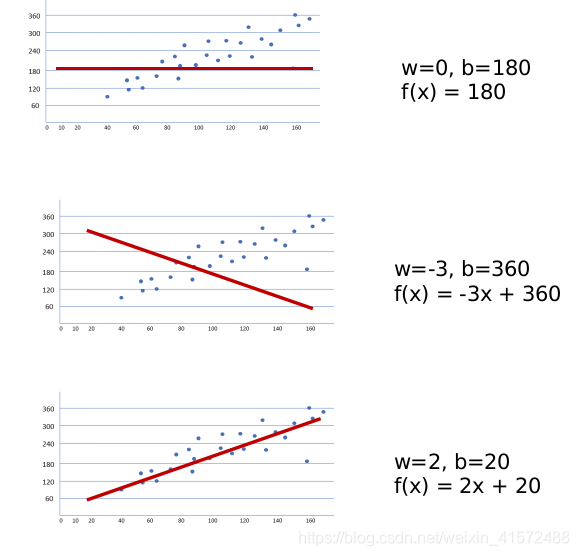
线性回归实际上要做的事情就是：选择合适的参数（θ0, θ1），使得hθ(x)方程，很好的拟合训练集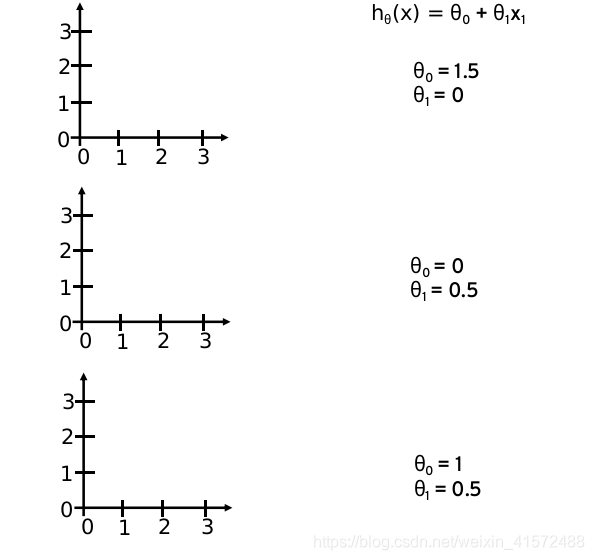在这里插入图片描述

在这里插入图片描述

梯度下降

梯度下降是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代的调整参数从而使损失函数最小化

假设你迷失在山上的浓雾之中，你能感觉到的只有你脚下路面的坡度。快速到达山脚的一个策略就是沿着最陡的方向下坡。这就是梯度下降的做法：通过测量参数向量θ相关的误差函数的局部梯度，并不断沿着降低梯度的方向调整，直到梯度降为0，到达最小值

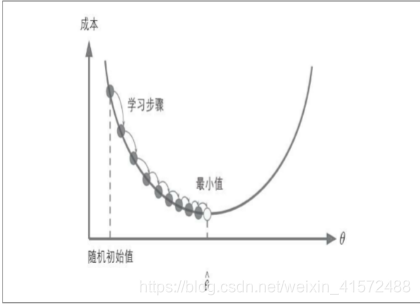
具体来说，首先使用一个随机的θ值（这被称为随机初始化），然后逐步改良，每次踏出一步，每一步都尝试降低一点损失函数（如MSE），直到算法收敛出一个最小值

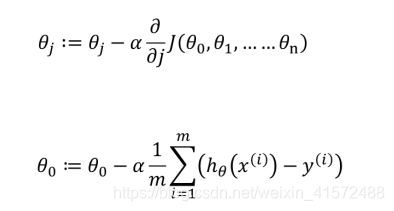
在这里插入图片描述

梯度下降的方向1：只要对损失函数求导，θ的变化方向永远趋近于损失函数的最小值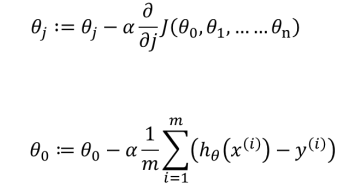在这里插入图片描述

梯度下降的方向2：如果θ已经在最低点，那么梯度将不会发生变化

在这里插入图片描述

梯度下降的步长1：梯度下降中一个重要参数是每一步的步长，这取决于超参数的学习率

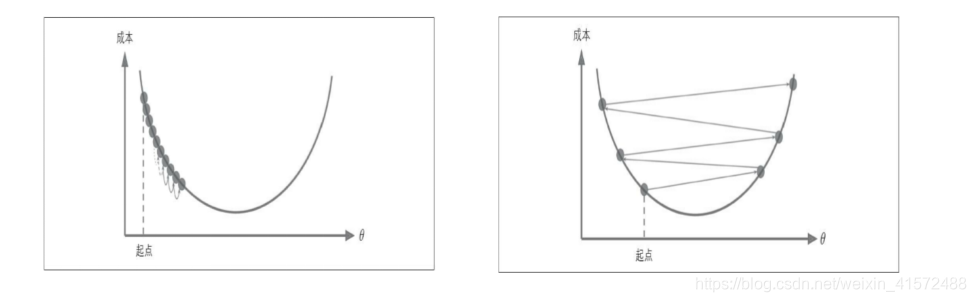
在这里插入图片描述
如果学习率太低，算法需要经过大量迭代才能收敛，这将耗费很长时间
如果学习率太高，那你可能会越过山谷直接到达山的另一边，甚至有可能比之前的起点还高。这会导致算法发散，值越来越大，最后无法找到好的解决方案

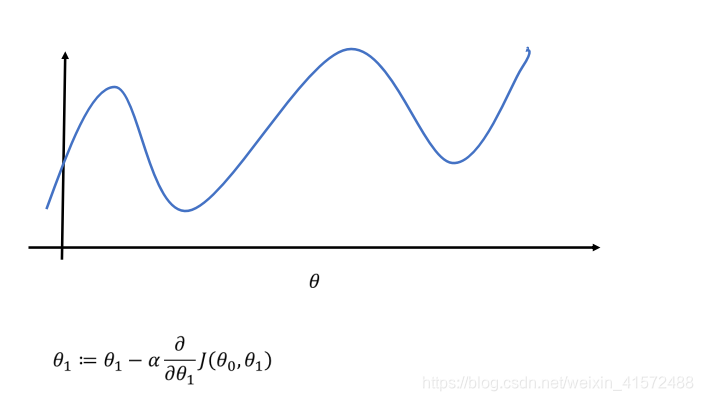
梯度下降的步长2：梯度下降的步长会逐渐变小在这里插入图片描述
梯度下降的局部最小值问题

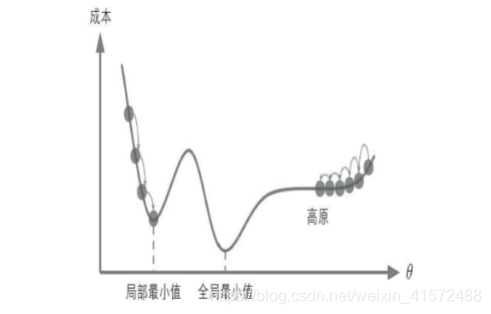
并不是所有的损失函数看起来都像是一个漂亮的碗，有的可能像山洞、山脉、高原或者各种不规则的地形，导致很难收敛到最小值。

比如上边这个图，如果随机初始值从左侧起步，那么会收敛到一个局部最小值，而不是全局最小值；如果算法从右侧起步，那么需要经过很长时间才能越过正整片高原。如果你停下得太早，将永远达不到全局最小值

梯度下降的局部最小值问题

如何应对？

1.对于MSE来说，因为损失函数是个凸函数，所以不存在局部最小值，只有一个全局最小值

通过随机初始化θ，可以避开局部最小值
对于多变量，高维度的值，就算在某个维度上陷入和局部最小值，但是还能从别的维度跳出

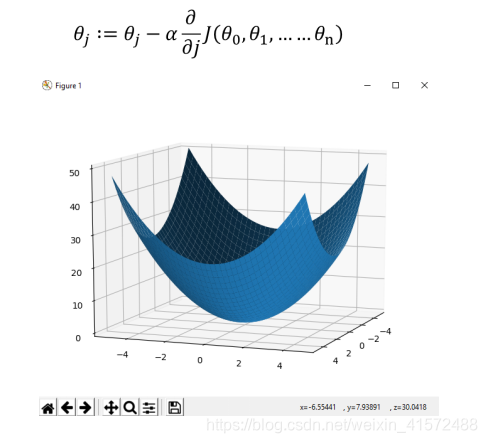
我们把梯度下降扩展到2维

扩展到2维以后，只要我们知道在每一个维度（分量）上的梯度下降情况，通过向量加和，我们也可以得到梯度在高维上整体的移动情况
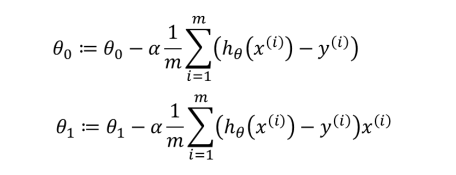
在这里插入图片描述

“Batch” Gradient Descent 批梯度下降
批梯度下降：指的是每下降一步，使用所有的训练集来计算梯度值

“Stochastic” Gradient Descent 随机梯度下降
随机梯度下降：指的是每下降一步，使用一条训练集来计算梯度值

“Mini-Batch” Gradient Descent “Mini-Batch”梯度下降
“Mini-Batch”梯度下降：指的是每下降一步，使用一部分的训练集来计算梯度值

多变量线性回归

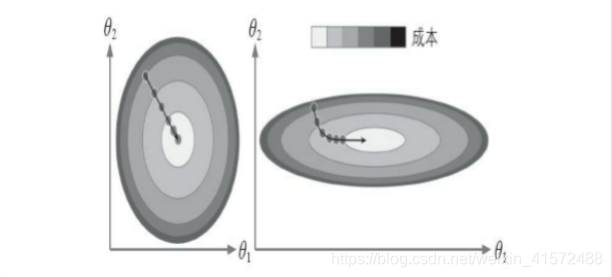
在这里插入图片描述

特征缩放（归一化）

在这里插入图片描述

左图的梯度下降算法直接走向最小值，可以快速到达。而在右图中，先是沿着与全局最小值方向近乎垂直的方向前进，接下来是一段几乎平坦的长长的山谷。最终还是会抵达最小值，但是这需要花费大量的时间

特征缩放是为了确保特征在一个数量级上

比如： x1 = 房屋面积（0-400 m2）
x2 = 卧室数量（1-5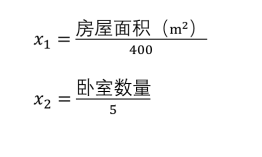）在这里插入图片描述

在这里插入图片描述

我们通常可以通过损失函数来确保梯度下降在正常工作

当损失函数上升的时候，证明梯度下降方法没有正常工作，这时候可以使用小一点的学习率α

对于足够小的学习率α而言，损失函数应该每次都下降
但是如果学习率α太小，收敛的速度将会很慢

随机梯度下降和‘Mini-batch’梯度下降

当我们做梯度下降的时候，用到了所有的数据，相当于求和取平均

“Batch” Gradient Descent 批梯度下降
批梯度下降：指的是每下降一步，使用所有的训练集来计算梯度值

“Stochastic” Gradient Descent 随机梯度下降
随机梯度下降：指的是每下降一步，使用一条训练集来计算梯度值

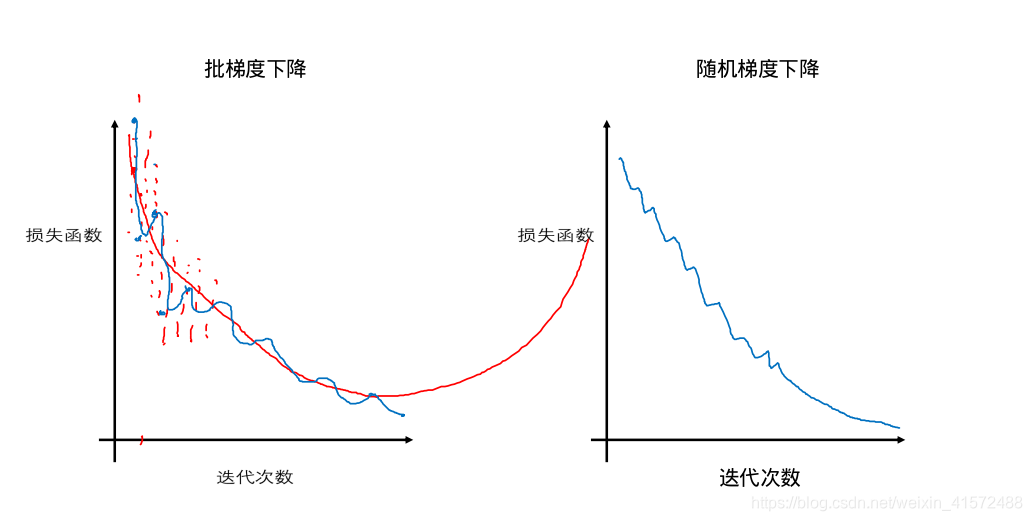
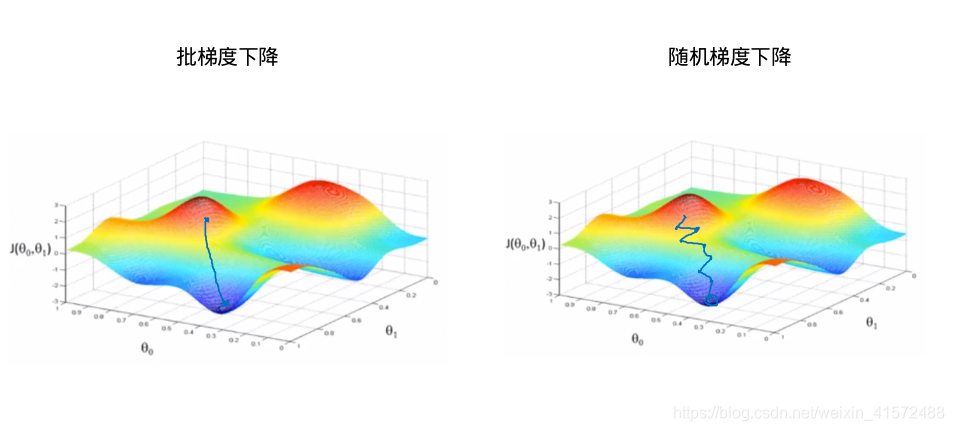
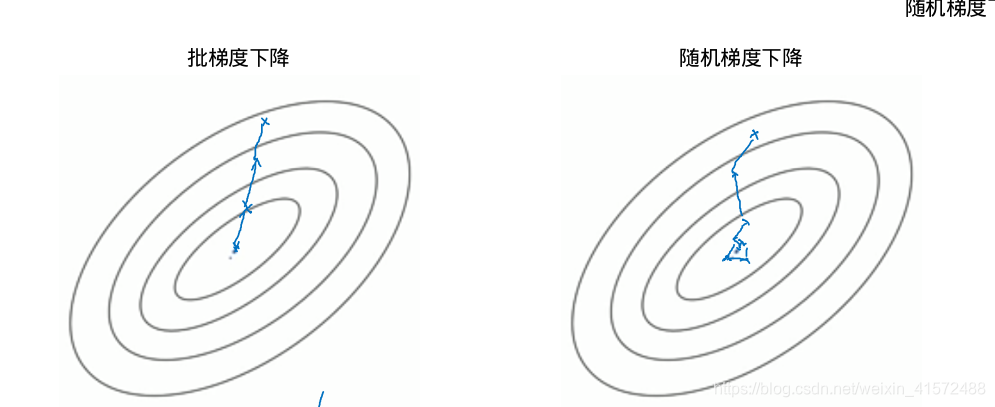在这里插入图片描述

在这里插入图片描述随机梯度下降思想：把m个样本分成m份，每次用1份做梯度下降；也就是说，当有m个样本时，批梯度下降只能做一次梯度下降，但是随机梯度下降可以做m次

‘Mini-batch’梯度下降

如果 mini-batch 大小 = m ：那他就是批梯度下降
如果 mini-batch 大小 = 1 ：那他就是随机梯度下降
如果 mini-batch 1 < 大小 < m ：那他就是‘Mini-batch’随机梯度下降

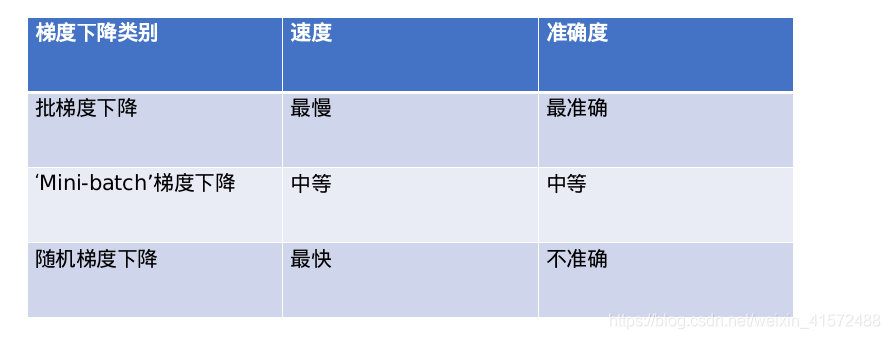
在这里插入图片描述
如何选择：
训练集比较小：使用批梯度下降（小于2000个）
训练集比较大：使用Mini-bitch梯度下降一般的Mini-batch size 是64，128,256， 512，1024
Mini-batch size要适用CPU/GPU的内存