通俗易懂--逻辑回归算法讲解(算法+案例)

寻觅互联网，少有机器学习通俗易懂之算法讲解、案例等，项目立于这一问题之上，整理一份基本算法讲解+案例于文档，供大家学习之。通俗易懂之文章亦不可以面概全，但凡有不正确或争议之处，望告知，自当不吝赐教！

GitHub地址(代码加数据)

1.逻辑回归(Logistic Regression)

1.1逻辑回归与线性回归的关系

逻辑回归是用来做分类算法的，大家都熟悉线性回归，一般形式是Y=aX+b，y的取值范围是[-∞, +∞]，有这么多取值，怎么进行分类呢？不用担心，伟大的数学家已经为我们找到了一个方法。

首先我们先来看一个函数，这个函数叫做Sigmoid函数：

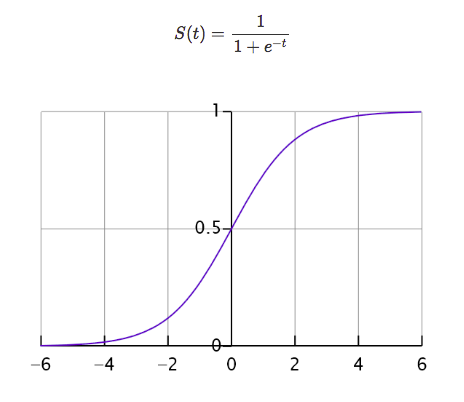
函数中t无论取什么值，其结果都在[0,-1]的区间内，回想一下，一个分类问题就有两种答案，一种是“是”，一种是“否”，那0对应着“否”，1对应着“是”，那又有人问了，你这不是[0,1]的区间吗，怎么会只有0和1呢？这个问题问得好，我们假设分类的阈值是0.5，那么超过0.5的归为1分类，低于0.5的归为0分类，阈值是可以自己设定的。

好了，接下来我们把aX+b带入t中就得到了我们的逻辑回归的一般模型方程：

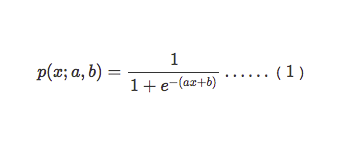
结果P也可以理解为概率，换句话说概率大于0.5的属于1分类，概率小于0.5的属于