机器学习-线性回归

本文参考吴恩达机器学习课程第2章

线性回归公式:

$f(x)={\theta }_0+{\theta }_{1}x$
代价公式(误差均值中的2用来抵消求导得来的2):
$J({\theta }_0,{\theta }_1)=\frac{1}{2m}{\sum }_{i=1}^m(f_{\theta }(x{)}^i-y^i{)}^2$

目标：代价最小化

这里演示单变量线性回归时:
令${\theta }_0=0$, $f(x)={\theta }_{1}x$
可对$J({\theta }_1)$求导,
$J^{{}^{\prime }}({\theta }_1)=\frac{1}{m}{\sum }_{i=1}^m({\theta }_1{x}^i-y^i)$
此时$J^{{}^{\prime }}({\theta }_1)=0$方可求出${\theta }_1$

实际上，由于代价函数经常含有2个及以上参数，目前函数处于三维空间x, y, z分别为${\theta }_0,{\theta }_1,J({\theta }_0,{\theta }_1)$，无法直接求导获得最佳参数组合
所以我们实际上，是不断尝试${\theta }_0,{\theta }_1$不同的值，找到损失结果最小的那组$({\theta }_0,{\theta }_1)$。
我们如何找到合适的尝试方法来找到这组参数呢,目前使用

梯度下降法

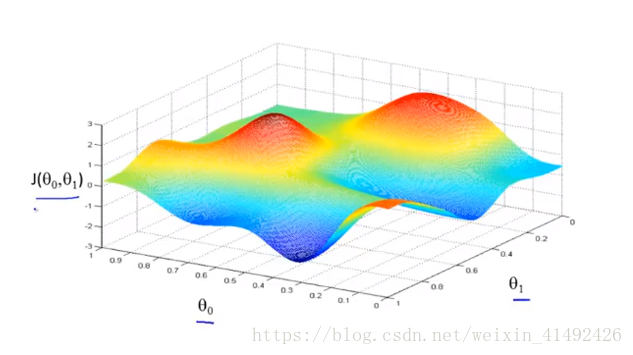
算法特点:从不同的起始值开始，获得的局部最优解是不一样
为了方便，设 ${\theta }_0=0,{\theta }_1=0$
$\alpha$为学习率(不变)，$\frac{d}{d{\theta }_i}J({\theta }_i)$为偏导数，参数更新公式:
${\theta }_i:={\theta }_i-\alpha \frac{d}{d{\theta }_i}J({\theta }_0,{\theta }_1)$($i=0,1$)

具体展开:
${\theta }_0:={\theta }_0-\alpha \frac{d}{d{\theta }_0}J({\theta }_0,{\theta }_1)={\theta }_0-\frac{1}{m}{\sum }_{i=1}^m({\theta }_0+{\theta }_1{x}^i-y^i)$
${\theta }_1:={\theta }_1-\alpha \frac{d}{d{\theta }_1}J({\theta }_0,{\theta }_1)={\theta }_0-\frac{1}{m}{\sum }_{i=1}^m({\theta }_0+{\theta }_1{x}^i-y^i)\ast x^i$

1. 导数项: 达到局部最优解时(图中某一处局部最低点时)，此时导数项为0，${\theta }_i:={\theta }_i-\alpha \ast 0$，参数不再更新,且随着$J(\theta )$接近最低点，导数项也会越来越小，所以暂时学习率可不变。
2. 梯度下降可以用于更新任何可微(因为需要求导)的代价函数J,目前使用的梯度下降用到了${\sum }_{i=1}m$，意味着每下降一次遍历一整个数据集，也称batch梯度下降算法。