C++交换排序之冒泡排序、快速排序

交换排序基本思想：将大值向一端移动，小值向一段移动。

#冒泡排序
基本思想：从头到尾依次对两个相邻的值进行比较，若为“逆序”则交换两 个的值。将序列按照此方法从头到尾处理一遍。
算法：

1. 第 i 个值与第 i+1 个值进行比较，若为逆序则交换他们 的值。
2. 将第 i+1 与第 i+2 个值进行比较，重复上面过程。
3. 上述过程为第一趟冒泡排序，进行一轮后，其结果是最大的值将排在最后的位置。
4. 同样方法进行第二趟排序，其结果是次大的数排在倒数第二位。
5. 依此，若有 n 个元素，则需经过 n-1 趟的比较和交换。
   

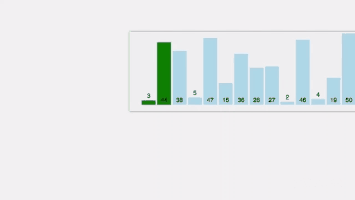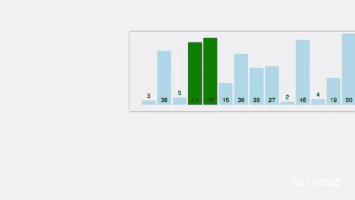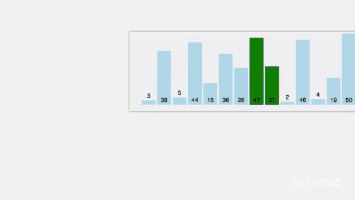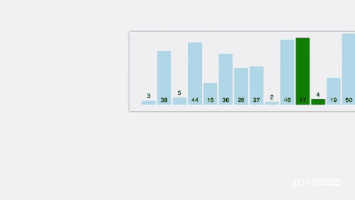
int n=15;
	int a[]={3,44,38,5,47,15,36,26,27,2,46,4,19,50,40};
//主干部分
	for(int i=0;i<n;i++)
		for(int j=0;j<n-i-1;j++)
			if(a[j]>a[j+1]){
				int temp=a[j];
				a[j]=a[j+1];
				a[j+1]=temp;}	

排序效率：
若记录序列的初始状态为"正序"，则冒泡排序过程只需进行一趟排序，在排序过程中只需进行n-1次比较，且不移动记录；反之，若记录序列的初始状态为"逆序"，则需进行n(n-1）/2次比较和记录移动。因此冒泡排序总的时间复杂度为O(n*n)。

当排序的数据比较多时冒泡排序的时间会明显延长。

#改进方法：快速排序
基本思想：

1. 从数列中选出一个数作为基准数（一般选择第一个数为基准数），从两头向中间进行比较交换，将基准值放在最终位置；
   2.将比基准数大的数全放到他的右边，小于他的数放在左边；
   3.再对左右区间重复进行操作二，直到个区间只剩一个数。
   算法思想：3,44,38,5,47,15,36,26,27,2,

0	1	2	3	4	5	6	7	8	9
3	44	38	5	47	15	36	26	27	2

定义三个参数：i,区间开始的地址；j 区间结束的地址，k 为中枢值（当前开始的值）,从左到右找比key大的值, 从右向左找比key小的值。

1. i=1, j=9, k=3

0	1	2	3	4	5	6	7	8	9
3	2	38	5	47	15	36	26	27	44

2. i=2(a[j]=38), j=1(a[j]=2), k=3,。由于i>j，故中枢值与 j 交换

0	1	2	3	4	5	6	7	8	9
2	3	38	5	47	15	36	26	27	44

3.排右半部分，k=38, i =4, j=8

2	3	4	5	6	7	8	9
38	5	27	15	36	26	47	44

4. i=8 , j=7 ,k=38，从a[j=8]开始，中枢值k与j交换

2	3	4	5	6	7	8	9
26	5	27	15	36	38	47	44

5. 数组分为两部分，一部分小于38，一部分大于38。 i=4, j=5, k=26

2	3	4	5	6
26	5	15	27	36

6. i =5 , j =4 , k=26，i>j, a[j]与k交换值

2	3	4	5	6
15	5	26	27	36

7. i=4,j=3,i>j, a[j]与k交换值

2	3	4	5	6
5	15	26	27	36

8. 38右半部分。i=8 , j=9 , k=47

8	9
44	47

最终得到结果：

0	1	2	3	4	5	6	7	8	9
2	3	5	15	26	27	36	38	44	47

void quickSort(int a[],int start,int end){
	if(start>=end) return;//只有一个数
	int i=start;
	int j=end+1;
	int key=a[start];
	while(true)
	{
		/*从左到右找比key大的值*/
      while(a[++i]<key)
	  {if(i==end){
		  break;
	  }}
	  /*从右向左找比key小的值*/
	   while(a[--j]>key)
	  {if(j==start){
		  break;
	  }}
     if(i>=j) break;
	 /*交换i,j对应的值*/
	 int temp = a[i];
	 a[i] = a[j];
	 a[j] = temp;}
	/*中枢值与j对应值交换*/
	int temp = a[start];
	a[start] = a[j];
	a[j] = temp;
	quickSort(a,start,j-1);//排j左边部分
	quickSort(a,j+1,end);//排j右半部分
}

排序效率：
（1）空间效率复杂度
快速排序是递归的，最优的情况下空间复杂度为：O(㏒₂n) ；每一次都平分数组的情况。
最差的情况下空间复杂度为：O( n ) ，退化为冒泡排序的情况
(2)时间复杂度：
快速排序最优的情况下时间复杂度为：O( nlog₂n )；
快速排序最差的情况下时间复杂度为：O( n^2 )。