如下图在不同的向量场内,如何评估闭合曲线s的积分
如图一曲线所在的向量场只有y分量,且向量场都是朝向y轴正方向
而我们知道点积F*dr,在同向时为正,垂直时为0,逆向时为负值,
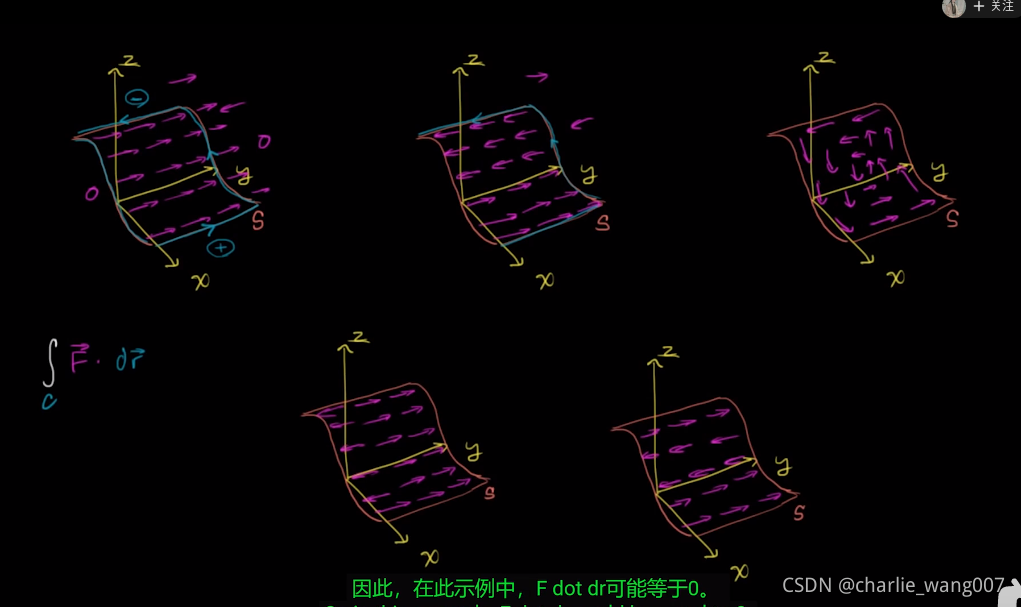
我们可以通过曲线附近的向量场的方向大体判断积分
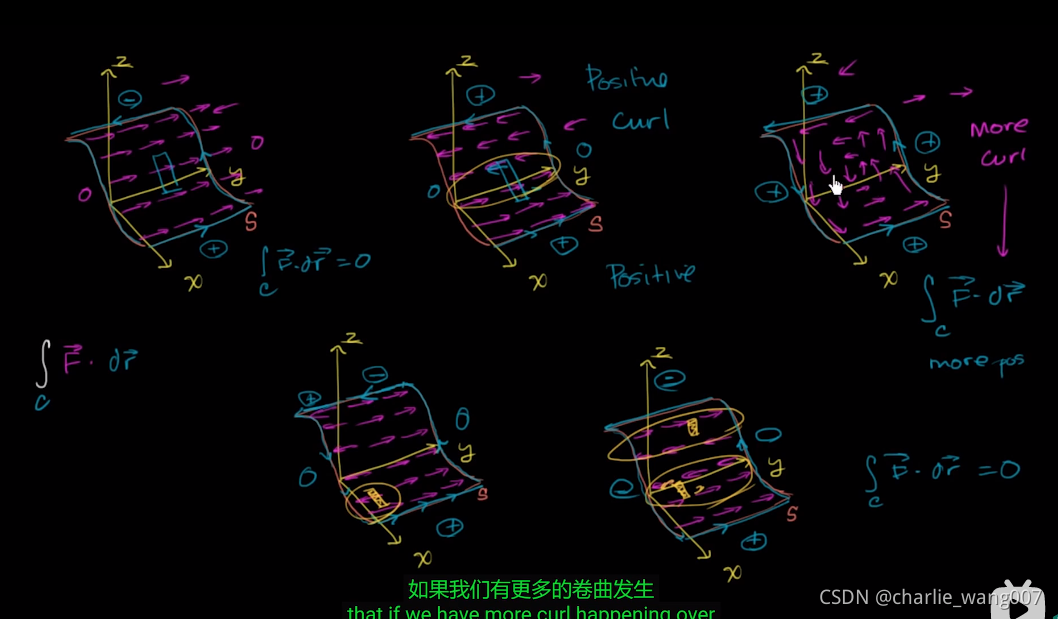
因此我们说三维向量场F内的闭合曲线s的积分,等于曲线围成的曲面内微小面积ds与旋度的积分
也等于通量的积分?
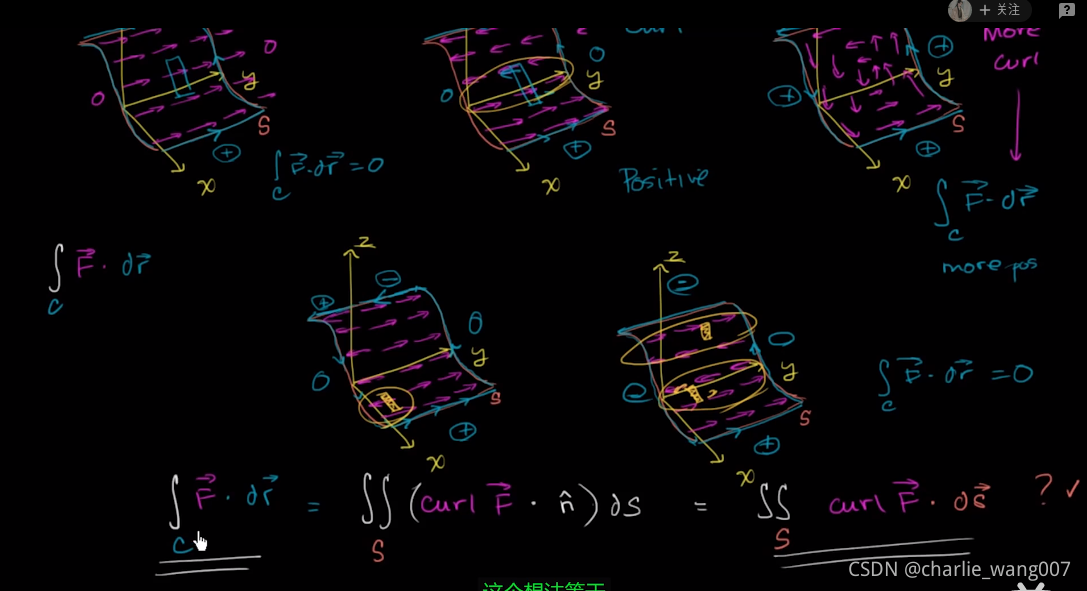
可以理解为stokes定理是格林定理向高维的推广
如下图在三维空间内的向量场F,曲线c所围城的面R
将z分量看做0
则通过计算F的旋度得到∫∫R(∂Q∂x−∂P∂y)ds\int\int_R(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})ds∫∫R(∂x∂Q−∂y∂P)ds

如何确定曲面的单位法向量方向:
想象我们沿着曲线行走,曲面总是在我们的左边,法向量是我们头顶所指的方向
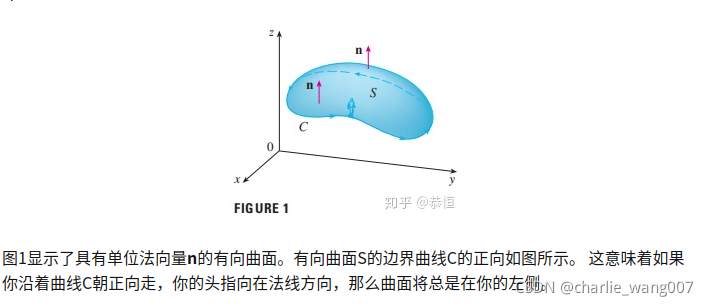
而如果我们的曲线几番方向顺时针的
则法向量朝向z轴负方向
比如拧瓶盖,逆时针时向上走,打开瓶盖,顺时针是向下走,盖上瓶盖
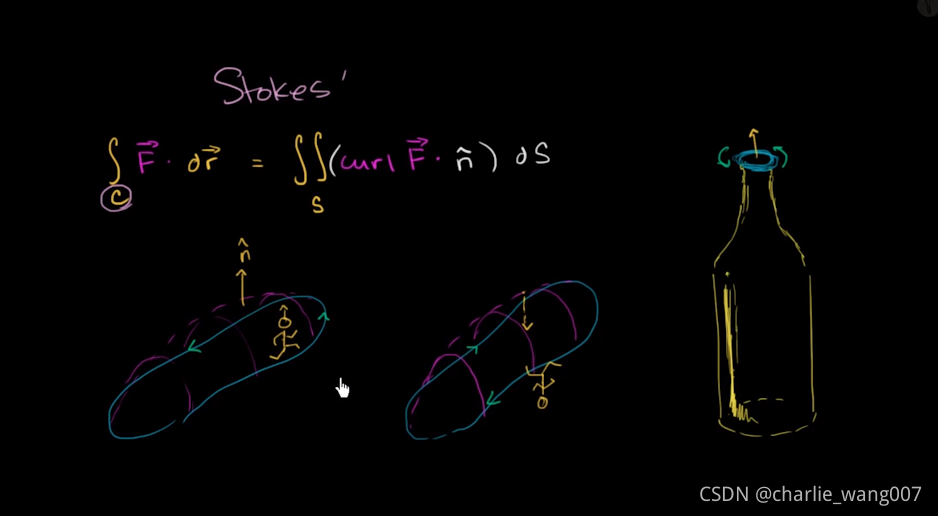
实例:
如下图我们有
曲线c关于x,y发函数
y+z=2
x2+y2=1x^2+y^2=1x2+y2=1
向量场F=−y2i+xj+z2k-y^2i+xj+z^2k−y2i+xj+z2k
如何求曲线c的积分
∫c=F⃗∗dr⃗=∫∫s(curlF⃗n)dS\int_c=\vec{F}*d\vec{r}=\int\int_s(curl \vec{F} n)dS∫c=F∗dr=∫∫s(curlFn)dS
先确定x,y,z以及边界,由单位圆确定角度和半径的边界
将xyz带入

而我们前面通量那节已经学习过法向量乘以ds等于ds⃗d\vec{s}ds

下面进行计算
取r的偏导
r为变量 theta为常数
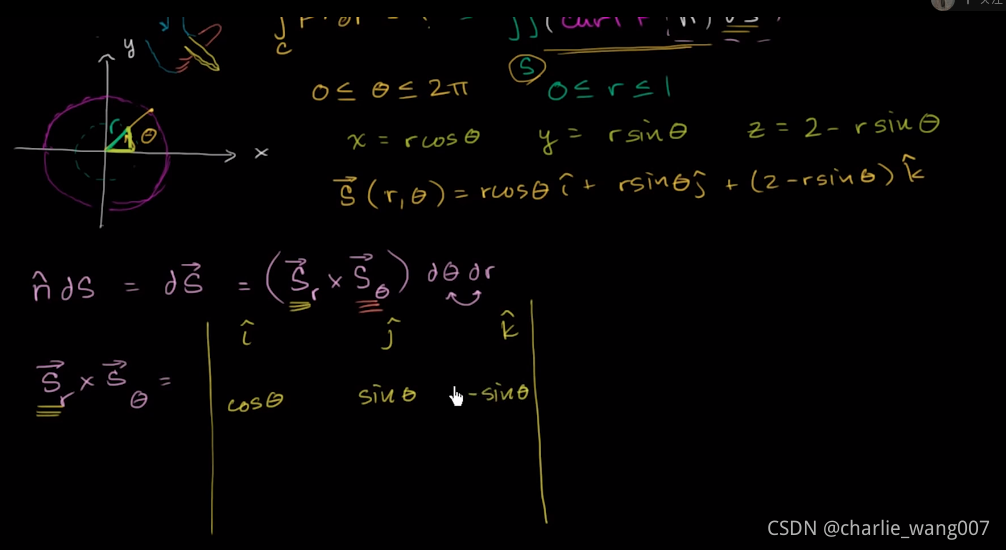
取theta偏导

取他们的叉积
(注意有点乘是取点积,没有点乘是取叉积,乘以标量是缩放)
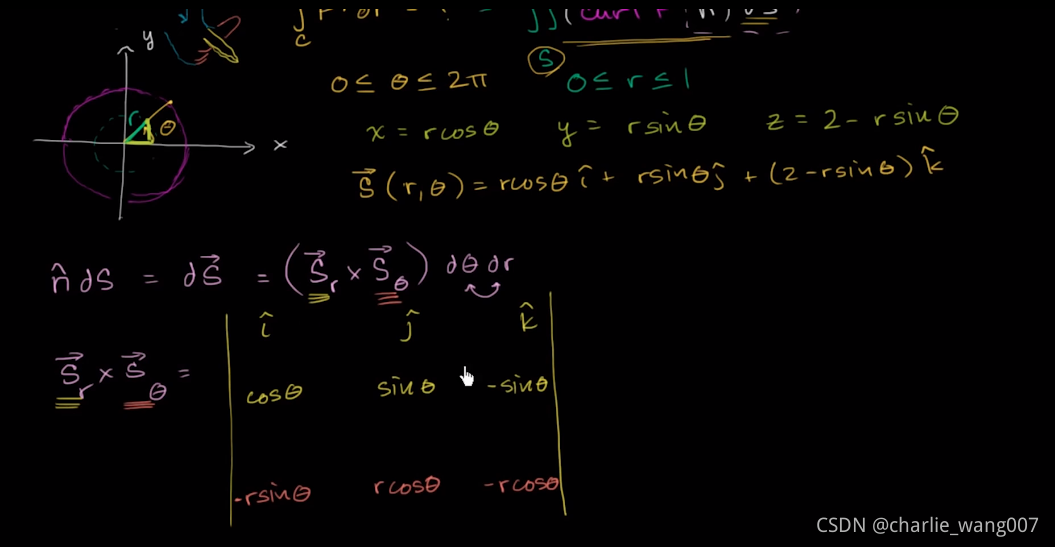
得到rj+rkrj+rkrj+rk
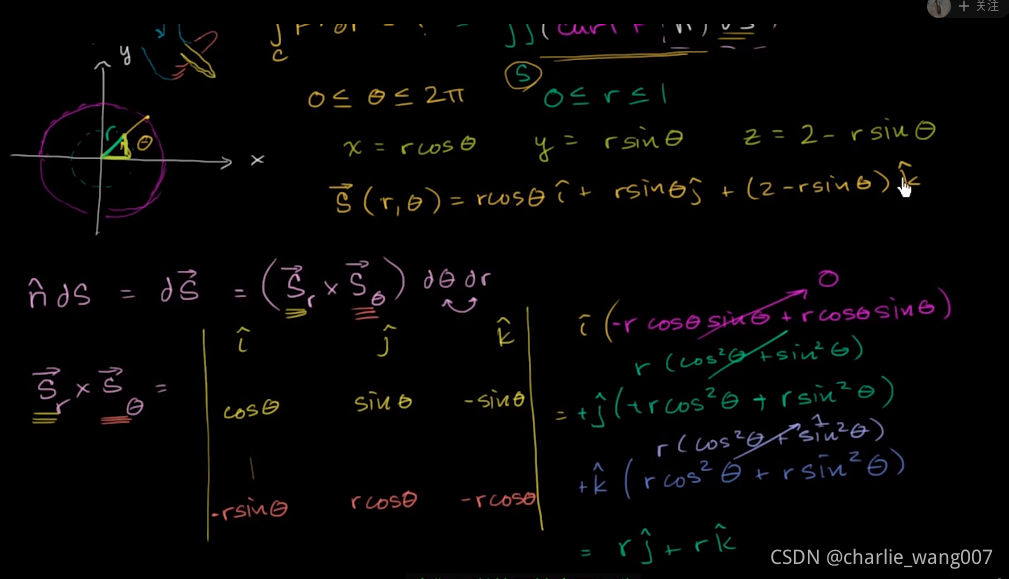
带入面积的双重积分
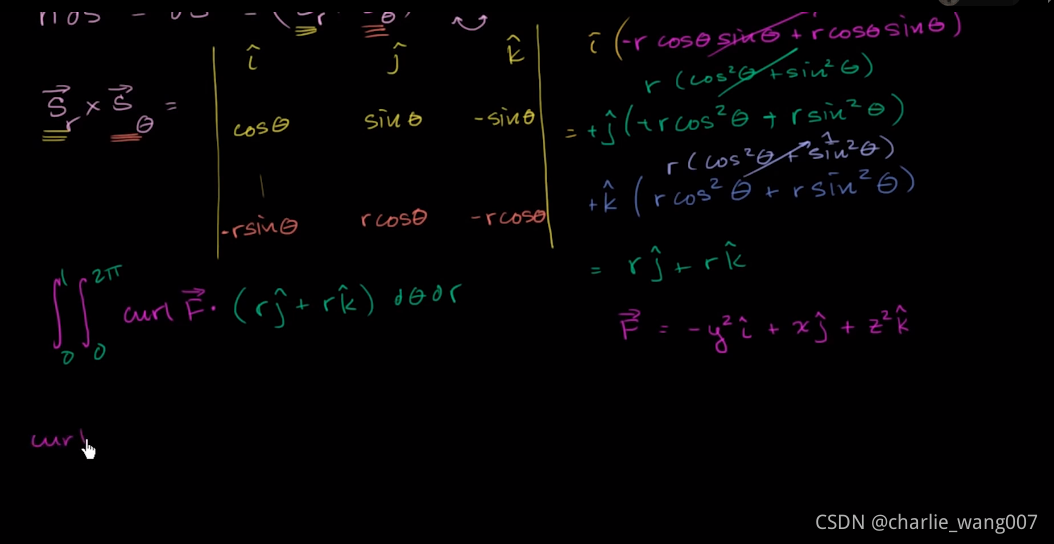
插入nabla算子与梯度,旋度,散度的关系


以上
∇\nabla∇算子作为标量的时候,本身就代表空间的梯度
∇\nabla∇与向量的点积,代表向量的散度
∇\nabla∇与向量的叉积,代表向量的旋度
取∇\nabla∇算子与向量F的叉积得到旋度
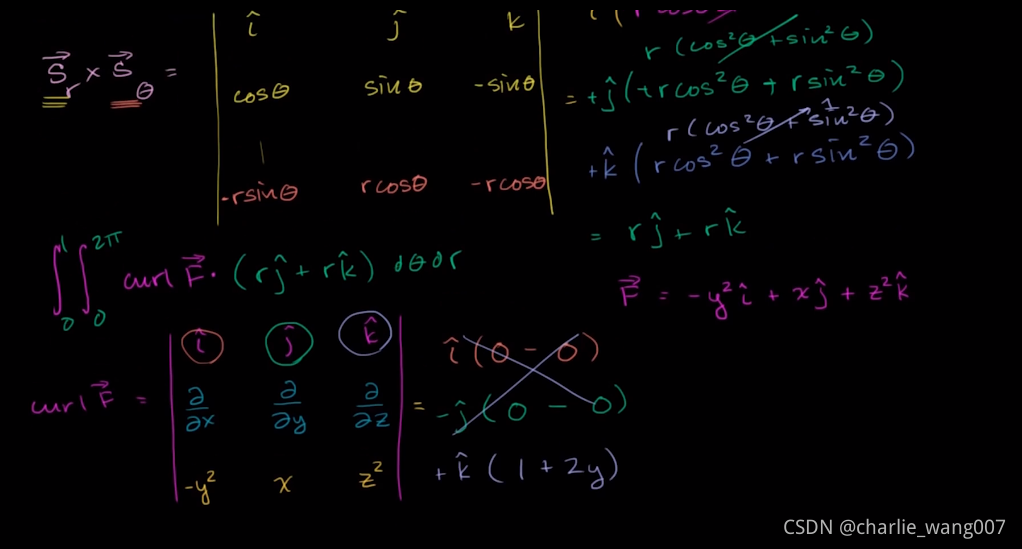
带入积分表达式
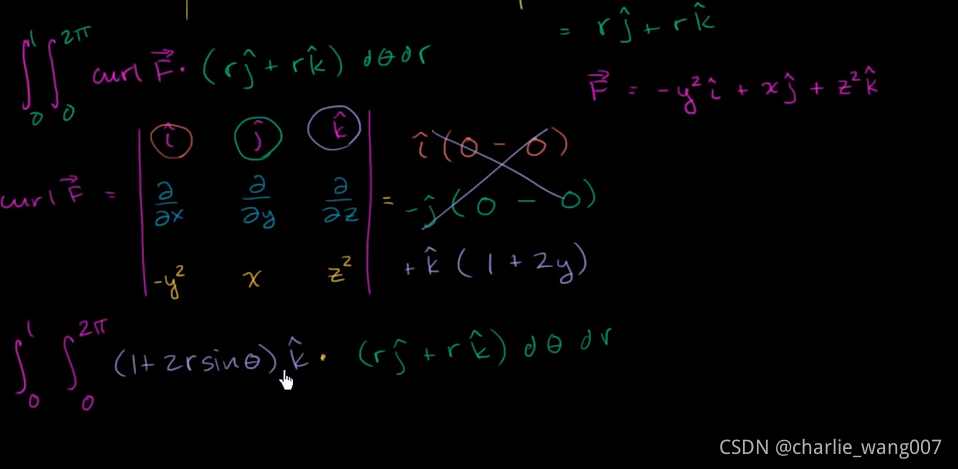
求出F与n的点积
再求theta的反导数
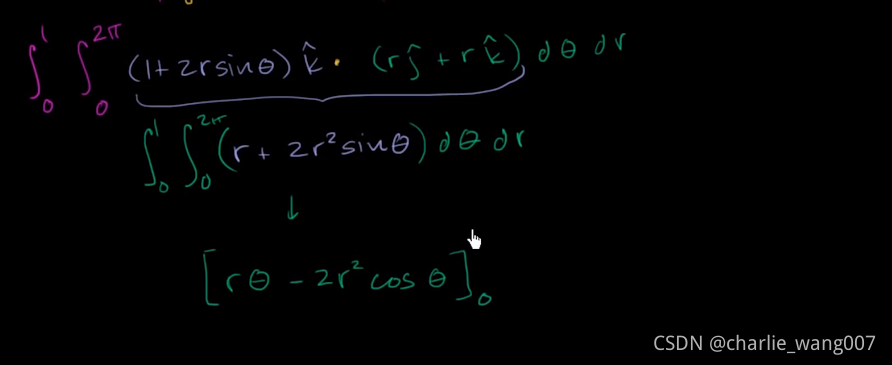

带入2pi和0积分
因为cos2π=cos0=1cos2\pi=cos0=1cos2π=cos0=1
得到2πr2\pi r2πr,它的原函数是πr2\pi r^2πr2
带入1和0积分
得到π\piπ
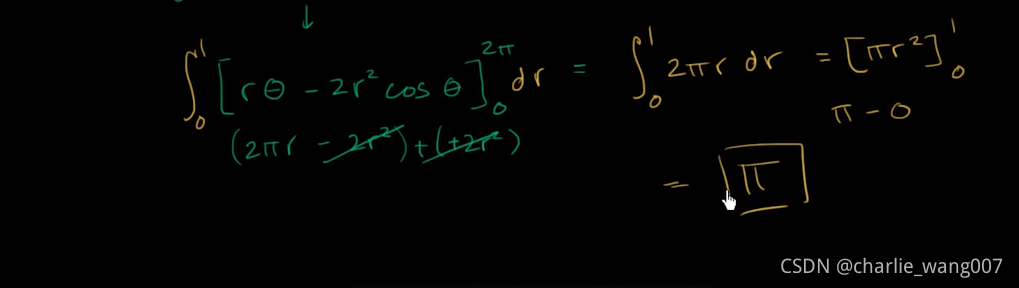
下面来看不用stokes定理如何计算c的积分
一般积分计算是向量场F与dr的点积,

我们已经参数化了xyz,将其带入表达式,再进行积分运算即可
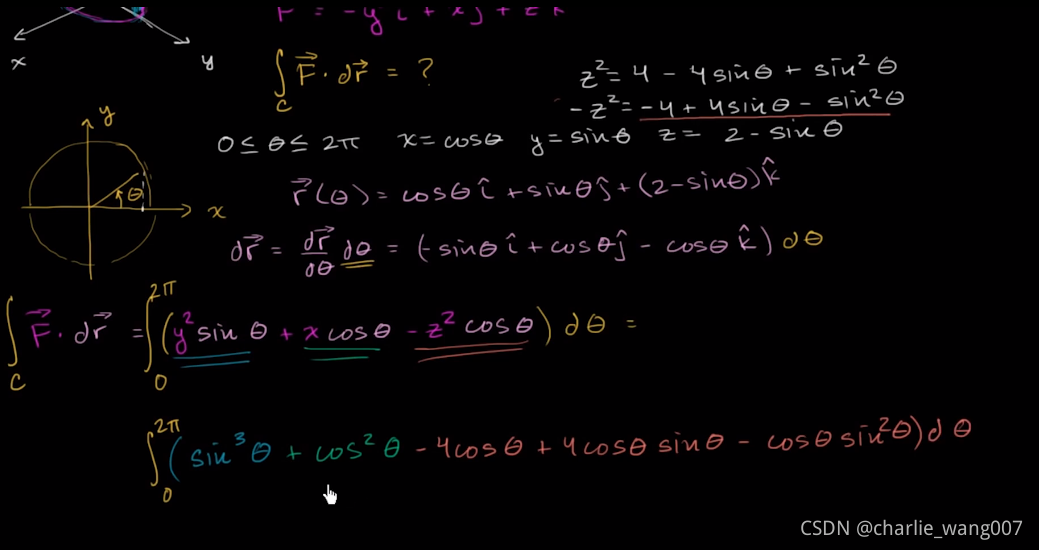








 本文介绍了如何在不同向量场中评估闭合曲线的积分,利用Stokes定理将三维空间中曲线积分转化为曲面积分。通过分析向量场的方向和曲线围成的曲面,确定法向量,并应用Stokes定理计算积分。以一个具体的例子展示了如何计算给定曲线的积分,同时讨论了不使用Stokes定理的常规积分计算方法。
本文介绍了如何在不同向量场中评估闭合曲线的积分,利用Stokes定理将三维空间中曲线积分转化为曲面积分。通过分析向量场的方向和曲线围成的曲面,确定法向量,并应用Stokes定理计算积分。以一个具体的例子展示了如何计算给定曲线的积分,同时讨论了不使用Stokes定理的常规积分计算方法。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








