对抗样本之JSMA原理&coding

最新推荐文章于 2025-02-05 18:59:46 发布

AI Bro

最新推荐文章于 2025-02-05 18:59:46 发布

阅读量5.7k

点赞数 8

分类专栏：深度学习 AI安全之对抗学习文章标签：对抗样本生成之JSMA JSMA代码实现 torch实现JSMA算法 JSMA原理详细解析对抗样本生成之有目标攻击

本文链接：https://blog.youkuaiyun.com/weixin_41466575/article/details/119024968

版权

1 引言

本文代码完成生成JSMA对抗样本的完整过程。直接复制代码就能跑。相信我，不骗你。
使用pytorch实现JSMA。pytorch不会？跳转
2016 论文地址

2 JSMA原理

与FGSM利用模型输出的损失函数梯度信息不同，JSMA主要利用模型的输出类别概率信息，来反向传播求得对应梯度信息。作者将其称为前向梯度。即：
通过如上的前向梯度，我们可以知道每个像素点对模型分类的结果的影响程度，进而利用前向梯度信息来更新干净样本 X，生成的对抗样本就能被分类成为指定的类别。作者宏观思维大体如此。
该论文引入显著图概念，即不同输入特征对分类结果的影响程度。

算法步骤：

1. 计算前向导数
计算模型类别置信度输出层中的每一个类别置信度对于输入X的偏导，该偏导值表示不同位置的像素点对分类结果的影响程度。
在这里插入图片描述
2. 构建显著图
分类器对于一个输入 x 的分类规则为：

假设分类器将 x 分为 j ，我们希望分为 t ，即

构建显著图（按照扰动方式的不同分有正向扰动与反向扰动）：

2.1. 正向扰动
在这里插入图片描述
2.2. 反向扰动

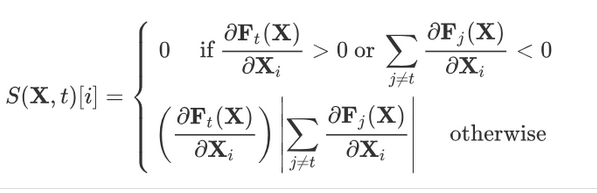
从而计算得到哪些像素位置的改变对目标分类 t 的影响最大。若对应位置导数值为正值（正向扰动），则增大该位置像素，可增加目标 t 分数；若对应位置导数值为负值（反向扰动），则减少该位置像素，可增加目标 t 分数。
至于正向扰动与反向扰动，在代码中作为超参数存在，一旦设定，说明要么干净样本只进行加操作，要么只进行减操作。

3. 使用显著图挑选需要改变的像素位置

作者经实践发现，找到单个满足要求的特征很困难，所以作者提出了另一种解决方案。通过显著图寻找对分类器特定输出影响程度最大的输入特征对，即每次计算得到两个特征。
大白话就是，在步骤 2 中构建的显著图里，找两个绝对值最大的点的像素位置，我们一次迭代只更新这两个像素。

Tips：
找到单个满足要求的特征困难，故提出寻找对特定输出影响最大的输入特征对。
干扰方式分为正向扰动和反向扰动。
JSMA算法为 L0，即修改程度不受限制，但修改的数量受到限制，是尽量减少对原样本修改像素的个数的算法。
由于修改的特征数有限，因此重复的次数需要被约束。
由于JSMA算法可针对具体特征修改，因此通常为定向攻击。通过特定的特征修改，使输出为特定输出。

3 coding

实验步骤：

训练一个简单模型（mnist手写数字分类任务）
通过该模型生成对抗样本
测试生成对抗样本的鲁棒性
可视化展示对抗样本效果

3.1 训练模型

from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

# 加载mnist数据集
# 定义数据转换格式,转化为（1，28*28）
mnist_transform = transforms.Compose([transforms.ToTensor(), transforms.Lambda(lambda x : x.resize_(28*28))])
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, download=True, transform=mnist_transform),
        batch_size=10, shuffle=True)
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True, transform=mnist_transform),
        batch_size=10, shuffle=True)

# 超参数设置
batch_size = 10
epoch = 1
learning_rate = 0.001
# 生成对抗样本的个数
adver_nums = 100

# LeNet Model definition
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(28*28, 300)
        self.fc2 = nn.Linear(300, 100)
        self.fc3 = nn.Linear(100, 10)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

# 选择设备
device = torch.device("cuda" if (torch.cuda.is_available()) else "cpu")

# 初始化网络，并定义优化器
simple_model = Net().to(device)
optimizer1 = torch.optim.SGD(simple_model.parameters(),lr = learning_rate,momentum=0.9)
print (simple_model)

Output：
在这里插入图片描述

如上代码，下载数据，设置超参数以及构建模型
如下代码，开始训练模型，并进行测试，观察模型准确率

# 训练模型
def train(model,optimizer):
  for i in range(epoch):
    for j,(data,target) in tqdm(enumerate(train_loader)):
      data = data.to(device)
      target = target.to(device)
      logit = model(data)
      loss = F.cross_entropy(logit