机器学习————神经网络的算法优化

神经网络的算法优化

TensorFlow

TensorFlow程序可以通过tf.device函数来制定运行每一个操作的设备

这个设备可以是本地的CPU或GPU，也可以是某一台远程的服务器
TensorFlow会给每一个可用的设备一个名称，tf.device函数可以通过设备的名称，来指定运算的设备，比如CPU在TensorFlow中的名称为/cpu:0

在默认情况下，即使机器有多个CPU，TensorFlow也不会区分它们，所有的CPU都是用/cpu:0作为名称

-而一台机器上不同GPU的名称是不同的，第n个GPU在TensorFlow中的名称为/gpu:n
-比如第一个GPU的名称为/gpu:0,第二个GPU名称为/gpu:1，以此类推
-TensorFlow提供了一个快捷的方式，来查看运行每一个运算的设备
-在生成会话时，可以通过设置log_device_placement参数来打印运行每一个运算的设备

-除了可以看到最后的计算结果之外，还可以看到类似“add:/job:localhost/replica:0/task:0/cpu:0“这样的输出
-这些输出显示了执行每一个运算的设备。比如加法操作add是通过CPU来运行的，因为它的设备名称中包含了/cpu:0
-在配置好GPU环境的TensorFlow中，如果操作没有明确的指定运行设备，那么TensorFlow会优先选择GPU

TensorFlow里的变量和常量

placeholder节点和Variable节点属于变量
使用placeholder()给输出的tensor指定数据类型，也可以选择指定形状
如果你指定None对于某一个维度，它的意思代表任意大小
这些节点特点是它们不真正的计算，他们只是在执行的过程中你要它们输出数据的时候去输出数据
constant：常量

正则化

Inverted DropOut反向随机失活

d3 = np.randm.rand(a3.shape[0], a3.shape[1]) < keep_prob

a3 = np.multiply(a3, d3)

a3 /= keep-prob

假设有50个神经元， keep-prob = 0.8， 也就意味着10个左右的神经元要设为0
在这种情况下， z = wa + b 就要减少20%， 这样呢，z会越来越小
为了弥补这种情况，我们需要对a进行弥补，弥补的方式就是用a/keep_prob

梯度下降的优化算法

指数加权平均

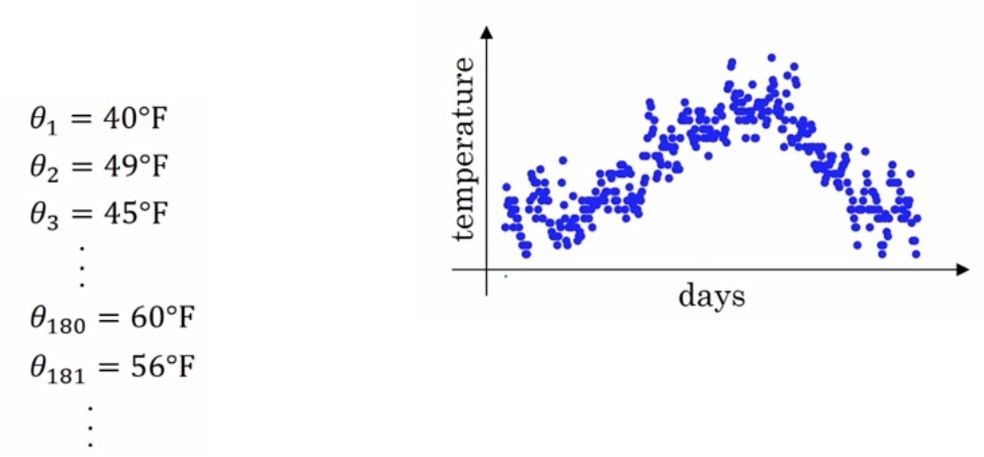
指数加权平均的作用

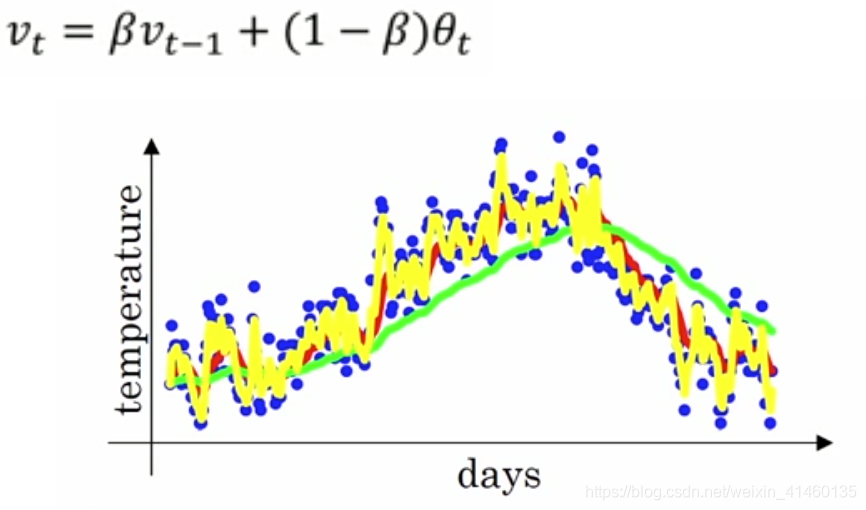
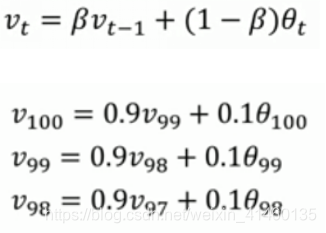
动量梯度算法

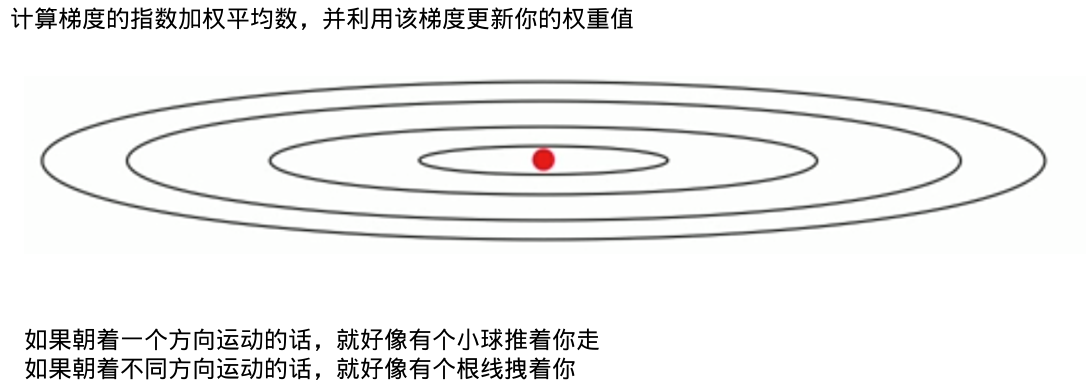
计算梯度的指数加权平均数，并利用该梯度更新你的权重值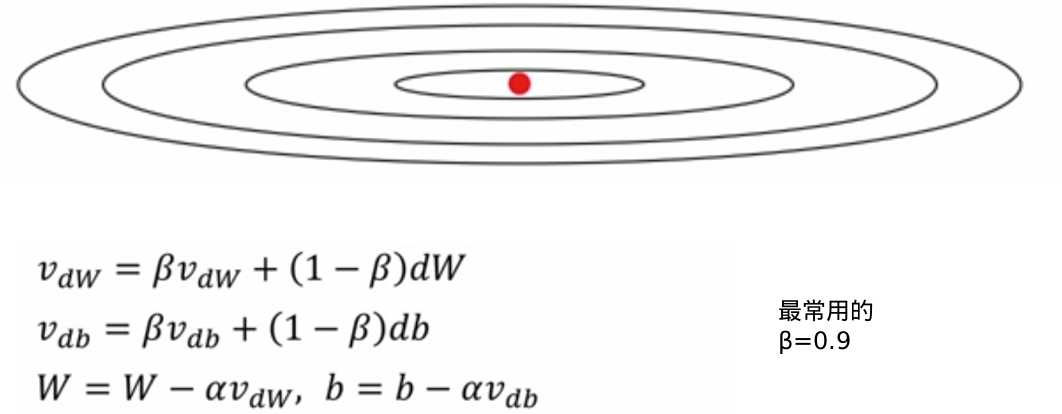

RMSprop

为了进一步优化损失函数在更新中存在摆动幅度过大的问题，并且进一步加快函数的收敛速度，RMSProp算法对权重 W 和偏置 bb的梯度使用了微分平方加权平均数。 其中，假设在第 t 轮迭代过程中，各个公式如下所示：

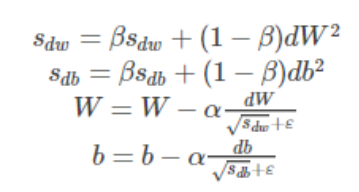
Adam

有了上面两种优化算法，一种可以使用类似于物理中的动量来累积梯度，另一种可以使得收敛速度更快同时使得波动的幅度更小。那么讲两种算法结合起来所取得的表现一定会更好。Adam（Adaptive Moment Estimation）算法是将Momentum算法和RMSProp算法结合起来使用的一种算法

Softmax

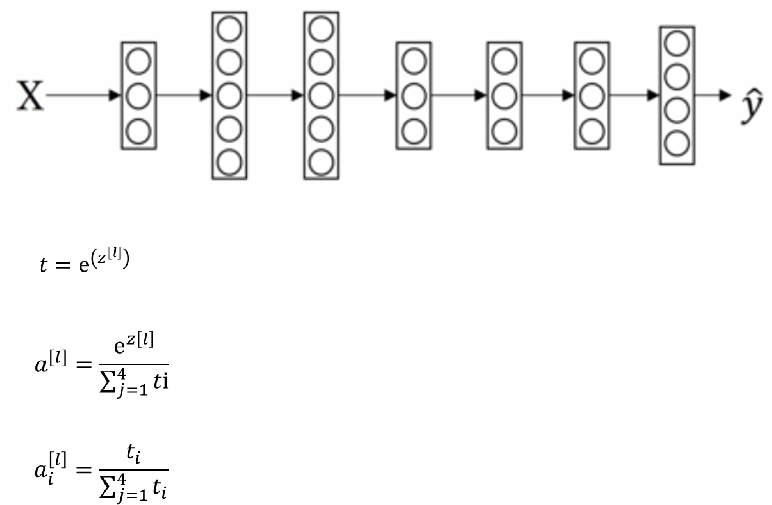
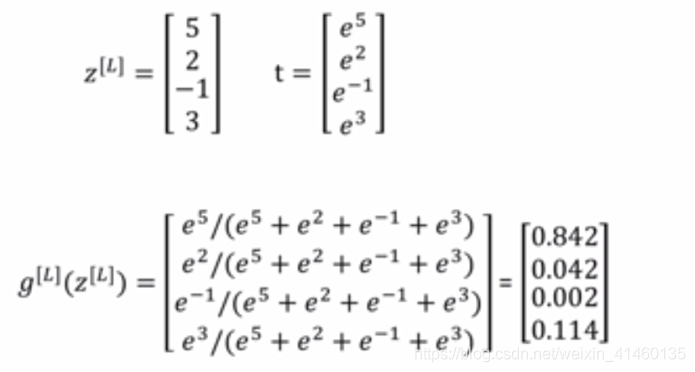
代码实现

tensorflow实现DNN

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
from tensorflow.contrib.layers import fully_connected
import matplotlib.pyplot as plt

# 构建图阶段
n_inputs = 28 * 28
n_hidden1 = 300
n_hidden2 = 100
n_outputs = 10

X = tf.placeholder(tf.float32, shape=(None, n_inputs), name='X')
y = tf.placeholder(tf.int64, shape=(None), name='y')


# 构建神经网络层，我们这里两个隐藏层，基本一样，除了输入inputs到每个神经元的连接不同
# 和神经元个数不同
# 输出层也非常相似，只是激活函数从ReLU变成了Softmax而已
# X输入数据， n_neurons神经元数量， name name_scope名字， activation是不是线性
def neuron_layer(X, n_neurons, name, activation=None):
    # 包含所有计算节点对于这一层，name_scope可写可不写
    with tf.name_scope(name):
        # 取输入矩阵的维度作为层的输入连接个数
        n_inputs = int(X.get_shape()[1])  # (1, 784)  784
        stddev = 2 / np.sqrt(n_inputs)    # 计算标准方差
        # 这层里面的w可以看成是二维数组，每个神经元对于一组w参数
        # truncated normal distribution 比 regular normal distribution的值小
        # 不会出现任何大的权重值，确保慢慢的稳健的训练
        # 使用这种标准方差会让收敛块
        # w参数需要随机，不能为0， 否则输出为0， 最后调整都是一个幅度没意义
        init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)
        w = tf.Variable(init, name='weights')
        b = tf.Variable(tf.zeros([n_neurons]), name='biases')
        # 向量表达的使用比一条一条加和要高效
        z = tf.matmul(X, w) + b
        if activation == 'relu':
            return tf.nn.relu(z)
        else:
            return z

with tf.name_scope("dnn"):
    hidden1 = neuron_layer(X, n_hidden1, 'hidden1', activation="relu")
    hidden2 = neuron_layer(hidden1, n_hidden2, "hidden2", activation="relu")
    # 进入到softmax之前的结果
    logits = neuron_layer(hidden2, n_outputs, "outputs")


# with tf.name_scope("dnn"):
#     # tensorflow使用这个函数帮助我们使用合适的初始化w和b的策略，默认使用ReLu激活函数
#     hidden1 = fully_connected(X, n_hidden1, scope="hidden1")
#     hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden2")
#     logits = fully_connected(hidden2, n_hidden2, scope="outputs", activation_fn=None)

with tf.name_scope("loss"):
    # 定义交叉熵损失函数，并且求个样本平均
    # 函数等价于先使用softmax损失函数，再接着计算交叉熵，并且更有效率
    # 类似的softmax_cross_entropy_with_logits只会给one-hot编码，我们使用的会给0-9分类号
    # 假设我们有十个值：1,2,3...0
    # 如果不用one-hot编码：1,2,3,...0
    # 如果用one-hot编码： 1： 1000000000， 2：0100000000，... 0: 0000000001
    xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)
    loss = tf.reduce_mean(xentropy, name="loss")

learning_rate = 0.01

with tf.name_scope("train"):
    optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    training_op = optimizer.minimize(loss)

with tf.name_scope("eval"):
    # 获取logits里面最大的那1位和y比较类别号是否相同，返回True或者False一组值；in=index
    correct = tf.nn.in_top_k(logits, y, 1)
    accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))

init = tf.global_variables_initializer()
saver = tf.train.Saver()

# 计算图运行阶段
mnist = input_data.read_data_sets("MNIST_data_bak/")

n_epochs = 100
batch_size = 50

with tf.Session() as sess:
    init.run()
    for epoch in range(n_epochs):
        for iteration in range(mnist.train.num_examples // batch_size):
            X_batch, y_batch = mnist.train.next_batch(batch_size)
            sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
        acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
        acc_test = accuracy.eval(feed_dict={X: mnist.test.images,
                                            y: mnist.test.labels})
        print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)

    save_path = saver.save(sess, "./my_dnn_model_final.ckpt")

"""
# 使用模型预测
"""
with tf.Session() as sess:
    saver.restore(sess, "./my_dnn_model_final.ckpt")
    X_new_scaled = mnist.train.images[2000].reshape(1, 784)

    # logits: softmax之前的值 0：2454， 1：1242， 。。。。9：7865
    # softmax之后的值： 0：0.25， 1：0.15，。。。，9：0.43
    y_pred = tf.argmax(logits, axis=1)  # 查看最大的类别是哪个
    Z = y_pred.eval(feed_dict={X: X_new_scaled})

    print(Z)

Softmax_regression

from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf

my_mnist = input_data.read_data_sets("MNIST_data_bak/", one_hot=True)

# The MNIST data is split into three parts:
# 55,000 data points of training data (mnist.train)
# 10,000 points of test data (mnist.test), and
# 5,000 points of validation data (mnist.validation).

# Each image is 28 pixels by 28 pixels

# 输入的是一堆图片，None表示不限输入条数，784表示每一张图片都是一个784个像素值的一维向量
# 所以输入的矩阵式None乘以784二维矩阵
x = tf.placeholder(dtype=tf.float32, shape=(None, 784))
# 初始化都是0， 二维矩阵784乘以10个W值
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

y = tf.nn.softmax(tf.matmul(x, W) + b)

# 训练
# label是每张图片都对应一个one-hot的10个值的向量
y_ = tf.placeholder(dtype=tf.float32, shape=(None, 10))
# 定义损失函数，交叉熵损失函数
# 对于多分类问题，通常使用交叉熵损失函数
# reduction_indices等价于axis，指明按照每行加，还是按照每列加
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)
# print(train_step)
# 评估

# tf.argmax()是一个从tensor中寻找最大值的序号，tf.argmax就是求各个预测的数字中概率最大的哪一个
# 0000001000  000100000
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))

# 用tf.cast将之前correct_prediction输出的bool值转换为float32，再求平均
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# 初始化变量
sess = tf.InteractiveSession()
tf.global_variables_initializer().run()
for _ in range(1000):
    batch_xs, batch_ys = my_mnist.train.next_batch(100)
    sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
    # print("TrainSet batch acc : %s " % accuracy.eval({x: batch_xs, y_: batch_ys}))
    # print("ValidSet acc : %s" % accuracy.eval({x: my_mnist.validation.images, y_: my_mnist.validation.labels}))

# 测试
print("TestSet acc : %s" % accuracy.eval({x: my_mnist.test.images, y_: my_mnist.test.labels}))
# 总结
# 1. 定义算法公式，也就是神经网络forward时的计算
# 2. 定义loss，选定优化器，并指定优化器优化loss
# 3. 迭代地对数据进行训练
# 4. 在测试集或验证集上对准确率进行评测