2024CSP-J模拟赛————S12678

禁止抄袭！！！

一，赛中得分

硬币（coin）	100
数位（digit）	100
划分（partition）	0
路径（path）	0
总分	200

二， 赛中概括

第一第二题30分钟做完，三四题不会。

三，题目解析

硬币（coin）

1.1 问题描述

小明很喜欢 100 这个数字，父母给他一些零花钱，这些零花钱的面值是 a 和 b，即小明有 x 个面值为 a 的硬币，y 个面值为 b 的硬币。小明想从中挑选一些硬币，这些硬币和的价值是 z，求 ∣z−100∣ 的最小值。

1.2 输入格式

从coin.in中读入数据。

一行包含四个整数 a,b,x,y。

1.3 输出格式

输出到coin.out中。

一行一个数，表示答案。

1.4 输入样例1

1

3

2

1

1.5 输出样例1

95

1.6 输入样例2

3

3

3

1

1.7 输出样例2

88

1.8 数据描述

对于测试点 1∼4：	1≤a,b≤5,0≤x,y≤5
对于测试点 5∼8：	1≤a,b≤10,0≤x,y≤10
对于测试点 9∼20:	1≤a,b≤100,0≤x,y≤100

模拟题，直接暴力，也可以01背包或多重背包

AC代码

#include<bits/stdc++.h>
using namespace std;
int main(){
    freopen("coin.in","r",stdin);
	freopen("coin.out","w",stdout);
	long long a,b,x,y,minn=9e18,cnt;
	cin>>a>>b>>x>>y;
	for(int i=0;i<=x;i++){//暴力
		for(int j=0;j<=y;j++){
			if(abs(a*i+b*j-100)<minn)minn=abs(a*i+b*j-100),cnt=a*i+b*j;
		}
	} 
	cout<<minn;
    return 0;
}

数位（digit）

2.1 问题描述

小明现在给你 n 个非负整数 a​1​​,a​2​​,..,a​n​​。

现在小明要求你把这 n 个非负整数从左到右按照十进制表示法写成一行。
然后现在小明会给你 q 次询问。

每次询问给你三个参数 l,r,x，问你a​l​​,a​l+1​​,...,a​r​​ 中数位 x 出现了多少次？

2.2 输入格式

从digit.in中读入数据。

第一行读入两个正整数n,q。

第二行读入 n 个非负整数，表示 a​1​​,a​2​​,..,a​n​​。

接下来 q 行，每行三个整数 l,r,x，表示对应询问。

2.3 输出格式

输出到digit.out中。

输出 q 行，从上到下依次表示对于每组询问的答案。

2.4 输入样例

5	5	//	无！！！	无！！！
30	0	123	0	53
1	2	0	无！！！	无！！！
1	4	0	无！！！	无！！！
2	4	0	无！！！	无！！！
1	5	3	无！！！	无！！！
1	5	1	无！！！	无！！！

2.5 输出样例

2

3

2

3

1

2.6 数据描述

对于测试点 1∼4:	1≤n,q≤1000,0≤a​i​​≤10​^9(1000000000)​​。
对于测试点 5∼8：	1≤n,q≤2×10^​5(100000)​​,0≤a​i​​≤1。
对于测试点 9∼20：	1≤n,q,≤2×10^​5(100000)​​,0≤a​i​​≤10^​9(1000000000)​​

 二位前缀和

#include<bits/stdc++.h>
using namespace std;
long long n,q,a[200005],b[200005][10];
int main(){
    freopen("digit.in","r",stdin);
	freopen("digit.out","w",stdout);
	cin>>n>>q;
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
		for(int j=0;j<=9;j++)b[i][j]=b[i-1][j];//继承之前的
		if(a[i]==0)b[i][0]++;
		while(a[i]){//拆数位+存前缀和
			b[i][a[i]%10]++;
			a[i]/=10;
		}
	}
	while(q--){
		long long l,r,x;
		scanf("%lld%lld%lld",&l,&r,&x);
		printf("%lld\n",b[r][x]-b[l-1][x]);//输出前缀和
	}
    fclose
    fclose
    return 0;

}

划分（partition）

3.1 问题描述

小明有一个长度为 n 的序列 a。

Alice和Bob玩一个关于这个序列的游戏。Alice和Bob交替从序列首部取一个连续段直至序列为空。例如序列是 [1,2,3,4,5]，Alice取 [1,2,3] 后序列变为 [4,5]，Bob取 [4,5] 后序列变为空序列。

Alice执行第一次操作。两人交替进行操作。

小明很喜欢 k 这个数字，要求每个连续段长度至少是 k，且至多是 2×k。每个连续段选出 k 个数，连续段的权值是选出的 k 个数的权值和的最大值。

如果序列长度小于 k，那么游戏立刻结束。

Alice取出的若干个连续段的权值和记为 x，Bob取出的若干个连续段的权值和为 y。Alice想最大化 x，Bob想最大化 y。假设两人采取最优策略，问 x−y 的值是多少。

3.2 输入格式

从partition.in中读入数据。

第一行输入两个正整数 n,k。

第二行输入 n 个数，表示序列 a。

3.3 输出格式

输出到partition.out中。

一行一个数表示最大值。

3.4 输入样例1

3	1	无！！！
8	5	6

3.5 输出样例1

2

3.6 输入样例2

7	2	无！！！	无！！！	无！！！	无！！！	无！！！
3	9	4	3	8	5	9

3.7 输出样例2

-1

3.8 数据描述

对于测试点 1∼4：	1≤k≤n≤10,1≤a​i​​≤10
对于测试点 5∼8：	1≤k≤n≤500,1≤a​i​​≤100
对于测试点 9∼20：	1≤k≤n≤2000,1≤a​i​​≤1000

3.9 数据下载

点击下载

（out文件丢了）

优先队列+DP（好难）

#include<bits/stdc++.h>
using namespace std;
long long n,k,a[2005],b[2005][2005],dp[20005][10];

int main(){
	cin>>n>>k;
	for(int i=1;i<=n;i++)cin>>a[i];
	for(long long i=1;i+k-1<=n;i++){
		priority_queue<long long,vector<long long>,greater<long long>> q;
		long long sum=0;
		for(int j=i;j<=i+k-1;j++){
			q.push(a[j]);
			sum+=a[j];
		}
		b[i][i+k-1]=sum;
		for(int j=i+k;j<=min(n,i+2*k-1);j++){
			if(a[j]>q.top()){
				sum=sum-q.top()+a[j];
				q.pop();
				q.push(a[j]);
				
			}
			b[i][j]=sum;
		}
	}
	for(long long i=n-k+1;i>=1;i--){
		dp[i][0]=-9e18;//A选
		dp[i][1]=9e18;//B选
		for(int j=i+k-1;j<=min(n,i+2*k-1);j++){
			dp[i][0]=max(dp[i][0],b[i][j]+dp[j+1][1]);
			dp[i][1]=min(dp[i][1],dp[j+1][0]-b[i][j]);
		}
	}
    cout<<dp[1][0];
    return 0;
}

路径（path）

4.1 问题描述

n×n的网格图，里面有 k 条线段，线段的斜率是 1 或者 −1。

网格图的每个网格是障碍或者空地。障碍不可以经过，空地可以经过。

线段经过的点表述为障碍

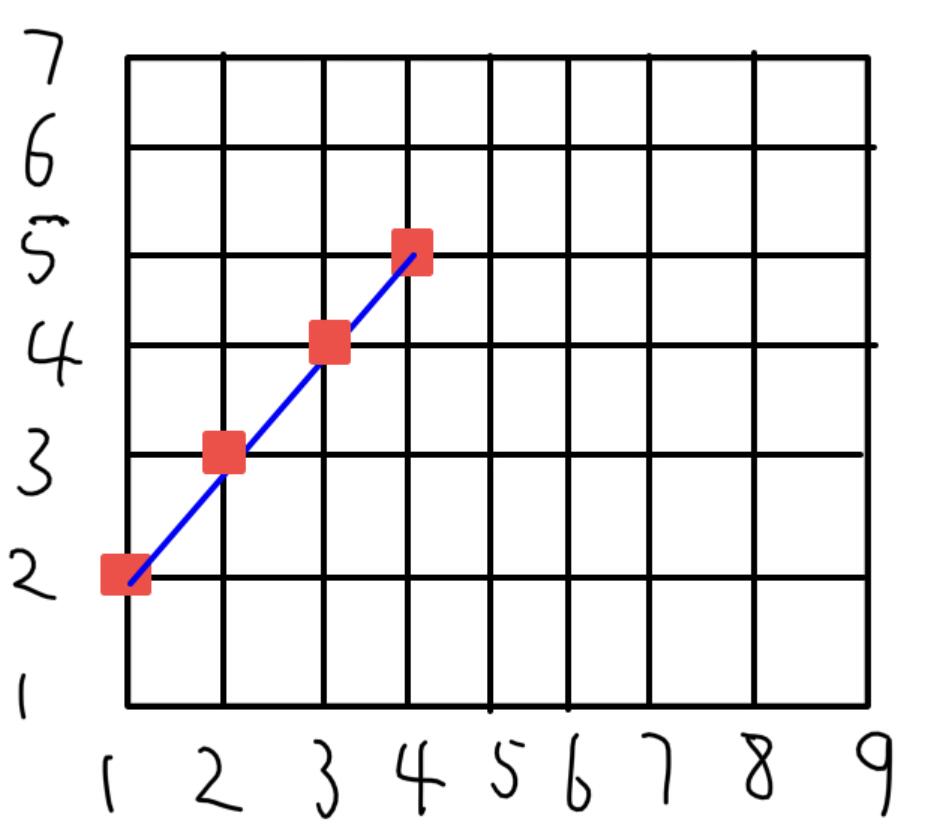
例如 (1,2),(4,5) 是一条斜率是 1 的线段。

q 个询问，每个询问包括两个整数 x,y，问 （1,x) 到 (n,y) 的最短路。

路径长度是从起点到终点经过的格点的个数。

保证起点和终点都没有线段阻挡。

如果从起点出发，不能到达终点，输出 −1。

4.2 输入格式

从path.in中读入数据。

第一行输入三个正整数 n,k,q。

接下来 k 行，每行四个正整数 x​1​​,y​1​​,x​2​​,y​2​​，分别表示线段的两个端点 ,(x​1​​,y​1​​),(x​2​​,y​2​​)。

接下来 q 行，每行两个正整数 x,y，表示询问。

4.3 输出格式

输出到path.out中。

共 q 行，每行一个整数表示答案。

4.4 输入样例

3	1	1	无！！！
1	2	2	3
1	3	无！！！	无！！！

4.5 输出样例

5

4.6 数据描述

对于测试点 1∼4：	1≤n≤1000,1≤k≤15,1≤q≤1
对于测试点 5∼8：	1≤n≤1000,1≤k≤15,1≤q≤10​^2(100)​​
对于测试点 9∼20：	1≤n≤1000,1≤k≤15,1≤q≤10​^5(100000)​​

代码没调出来，所以没有AC代码