机器学习算法（二）逻辑回归 （Logistic Regression）

逻辑回归属于有监督学习的分类算法

1、概要介绍

（1）回归：假设有一些数据点，我们用一条直线对这些点进行拟合，这个拟合的过程就是回归。

拟合：把平面上的一些点用一条光滑的曲线连起来。

（2）逻辑回归

通过将数据拟合进一个逻辑函数来预估一个事件出现的概率（输出值在0~1之间），P>0.5的数据被分为1类，P<0.5的数据被分为0类。

2.原理说明

（1）Logistic回归的主要思想：

根据现有的数据，对分类边界线建立回归公式，以此进行分类。

（2）Logistic回归的过程

a.收集数据

b.分析数据

c.训练算法，为找到最佳回归系数

d.测试算法

3、算法推导

逻辑回归的最终结果是一组特征的系数：，其中就是系数。

（1）回归函数

sigmoid函数： 

  

这里的x就是前面的z

它对x的导数：

值域在0~1之间

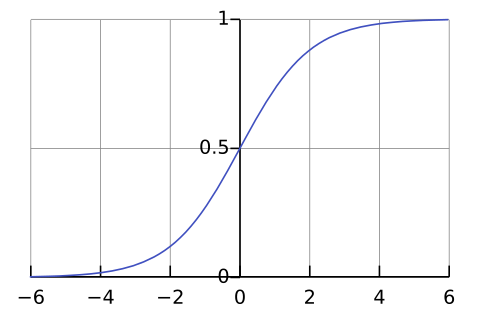
（2）为实现Logistic回归分类器，可以在每个特征上都乘以一个回归系数，然后将所有的结果加起来，将总和代入到sigmoid函数中，即可得到一个0~1之间的值，确定分类器后，要确定最佳回归系数（weight）。sigmoid函数的输入采取向量的写法上式记为,向量x为分类器输入数据，向量w就是要找的最佳回归系数。

注：的参数z是一组列向量，故实现时要支持列项作为参数，并返回列向量。

（3）优化方法——寻找最佳回归系数

1）梯度上升和梯度下降法

梯度上升求最大值，梯度下降求最小值

要找到某函数的最大值，最好的方法是沿着该函数的梯度方向寻找，梯度（），的梯度

（4）训练算法（目的：使用优化算法找到最佳回归系数）

1）在数据集通过梯度上升法找到最佳回归系数，也就是拟合出Logistic回归模型的最佳参数

梯度上升伪代码：

每个回归系数初始化为1：

重复R次：

              计算整个数据集的梯度

              使用alpha gradient更新回归系数的向量

返回回归系数

alpha是向目标移动的步长

2）构造预测函数

判定边界（）对不同类别的数据进行分割的边界）：

最佳参数是

预测函数：

函数的值就是结果为类别1的概率。