快速傅里叶变换（FFT）

快速傅里叶变换（FFT）是一种高效的算法，用于计算离散傅里叶变换（DFT）。FFT由J.W.库利和T.W.图基在1965年提出，其主要目的是减少计算DFT所需的乘法次数，从而显著提高计算效率。与传统的DFT相比，FFT将DFT的复杂度从O(N^2)降低到O(N log N)，特别是在处理大量数据时，这种改进极为显著。

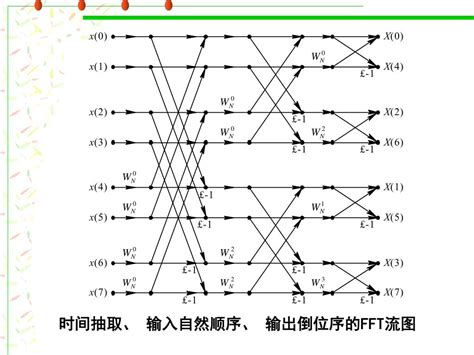
FFT的基本思想是利用DFT的对称性和周期性，通过分治策略将长序列的DFT分解为短序列的DFT，从而减少计算量。具体来说，FFT将输入信号分为偶数索引和奇数索引两部分，分别递归进行FFT，然后合并得到最终结果。此外，FFT还利用了单位根的性质，通过迭代求解、蝴蝶操作等方法进一步优化计算过程。

FFT在多个领域有着广泛的应用，包括信号处理、图像压缩、音频编码解码、雷达系统、地震勘探等。例如，在音频处理中，FFT可以用于频率分析和滤波器设计；在图像处理中，FFT常用于图像压缩和去噪。

总之，快速傅里叶变换（FFT）是一种重要的数学工具，它通过减少计算量，使得大规模数据的傅里叶变换成为可能，并在多个科学和工程领域中得到了广泛应用.

快速傅里叶变换（FFT）的历史发展和J.W.库利与T.W.图基的贡献是什么？

快速傅里叶变换（FFT）的历史发展可以追溯到19世纪，但其现代形式主要由J.W.库利和T.W.图基在1965年提出。这一算法的提出极大地推动了数字信号处理技术的发展，并在多个领域得到了广泛应用。

FFT算法的基本思想是将一个长序列的离散傅里叶变换（DFT）分解为两个较短序列的DFT，从而显著降低计算复杂度