昨天赶在ddl之前(也不算啦,上午就都完成了)把week two的课程内容和要完成的作业(must and optional)都做完了,赶紧写篇博客来总结分享一下学习到的芝士。
Linear regression with multiple variables
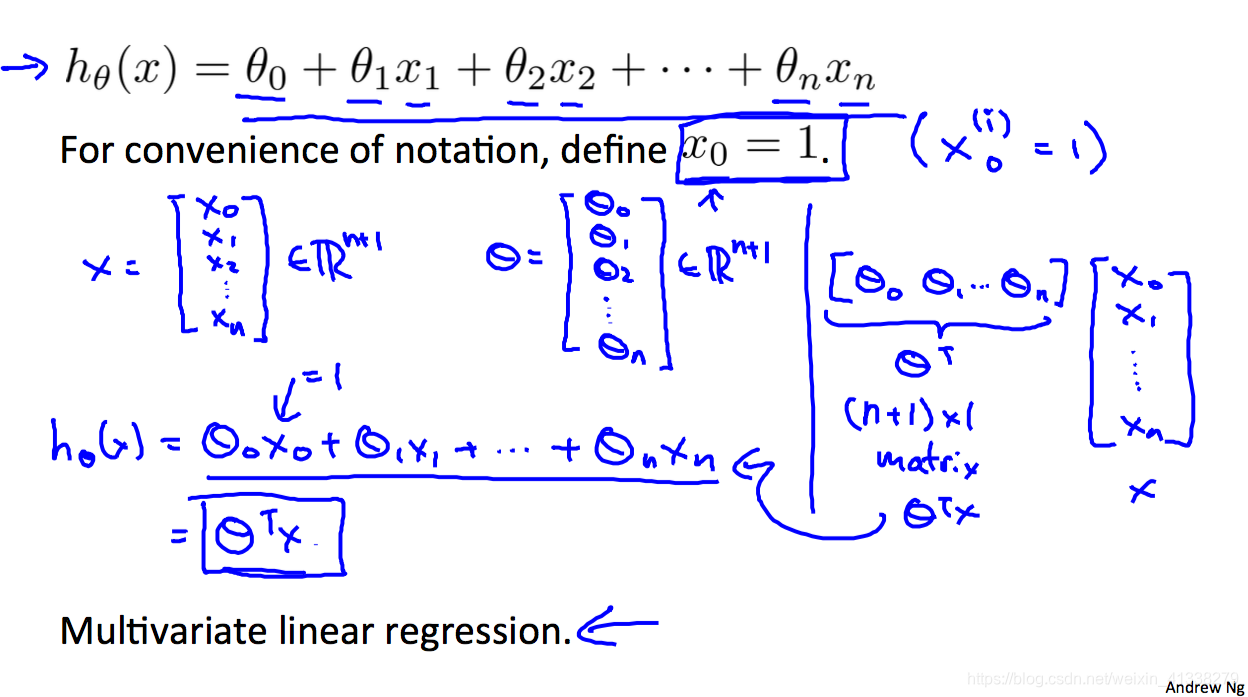
多输入变量的线性回归其实和最开始学习的最基本、简单的single variable是类似的,只不过现在input vector的dimension大于2(the input with single variable加上了一列1所以是two-dimensional vector)规模更大罢了,其他都还是一样的。
下面是该模型的hypothesis,应该非常眼熟啦!
Gradient descent for multiple variables
也和之前的是一样的,只不过每次迭代更新的参数个数更多一些,对了一定要是同时更新,simultaneously.

Feature scaling & Mean normalization
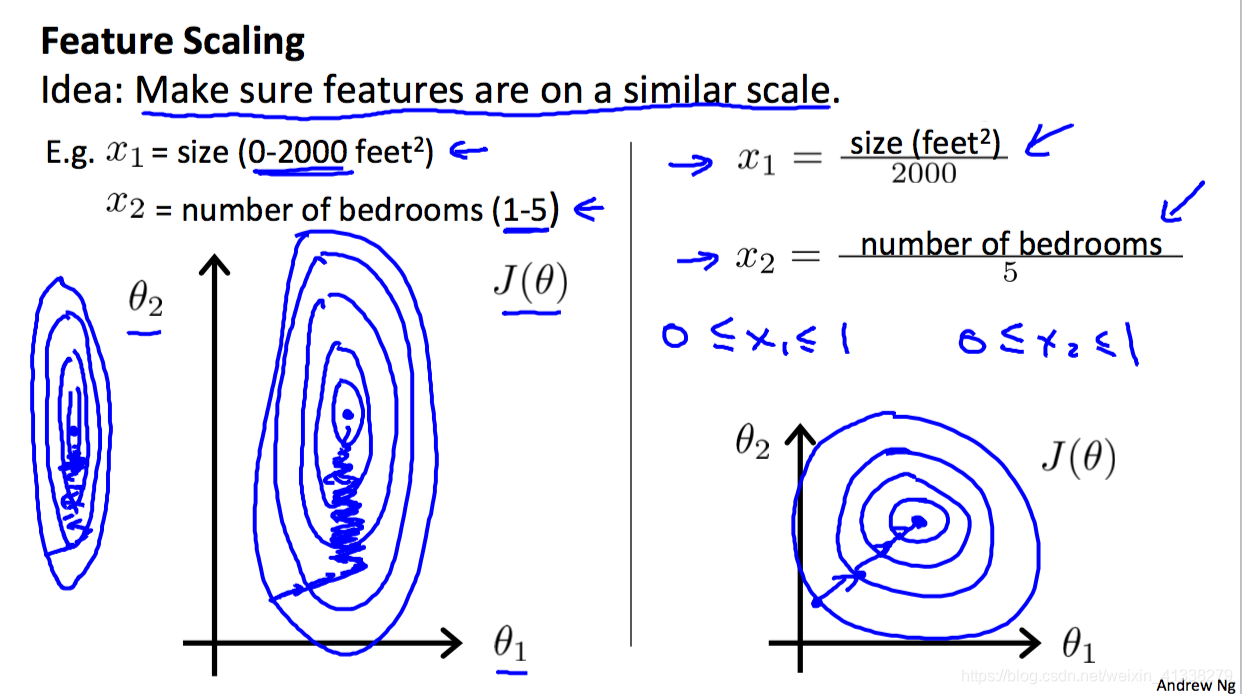
这两个对于特征的处理操作方法太重要了,它们是为了保证多变量的取值范围尽量相似(make sure features are on a similar scale),目标是加快cost function的收敛速度,换句话来说就是快点找到objective function。这里有两种常见的操作,第一种是feature scaling;第二种是mean normalization。
Feature scaling
Get every feature into approximately a [-1, 1] range
将每一个特征的取值范围处理到[-1, 1]这个区间内。
具体怎么实现呢,很简单,就是把数据集中某一个特征的所有值分别/(特征的最大值-特征的最小值),这里提醒一下X0是不需要处理的,本来也都是1(X0=1)。还有一点需要注意的是,虽然这里的目标是将取值范围处理到[-1, 1]这个范围内,但并不需要严格执行,只要保证不同特征之间的取值范围不要相差上百、千个数量级就好,就算有个特征的取值范围是[-2, 5]也是ok不需要进一步处理的,非要处理也没有关系,只是处理前后对cost function收敛的速度并没有多大的影响,有点多此一举。
Mean normalization
Replace X with X-μ to make features have approximately zero mean(Do not apply to X0)
这是第二种方法,目标是让各个特征的均值为0,实现办法其实就是将feature scaling的公式的分子X 换成 X-μ(μ为平均值),分母是(max-min)不变,也可以是标准平方差(standard deviation)。

Learning rate
介绍完了两种处理输入变量进而让cost function收敛速度更快的方法后,还有一个手动设置的参数learning rate,其对cost function收敛的趋势和效果也是有非常重大影响的。这就引入了两个问题:1)how to make sure gradient descent is working correctly? 2)how to choose appropriate value for learning rate?
不急,跟着Andrew老师来一个个分析解决吧?
1)how to make sure gradient descent is working correctly?
其实我们希望看到的结果就是,随着迭代次数的增加,cost function的值是越来越小的。
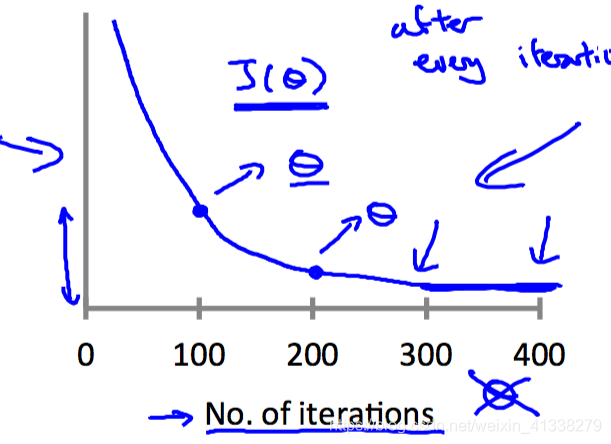
所以可以通过画一个以迭代次数为横坐标(No. of iterations as horizontal axias),cost function的值为纵坐标(values of cost function as vertical axias)的二维图,将gradient descent的过程可视化出来,通过观察曲线图的走向和变化趋势,就可以判断gradient descent是否正常工作了。
如果出现下面这种和预期不符的图,则说明是learning rate的取值不够合适。
- cost function的值随着迭代次数越来越大,根本没有收敛(convergent)的迹象,反而发散(diverse);
- cost function的值忽大忽小,上下波动;
- cost function的值不断下降,不过趋向收敛的速度很慢。
第一种情况的出现是因为learning rate取值太大了,所以在gradient descent的时候,参数更新的幅度太大,跨过了global optimum,到达了另外斜率更大的一边,结果更新幅度更大,又大步跨向了另一边,于是参数的取值让cost function的值越来越大,无法收敛,向外发散。
第二种情况也是learning rate取值比较大,值忽大忽小这种情况的产生也取决于参数初始的值为多少。
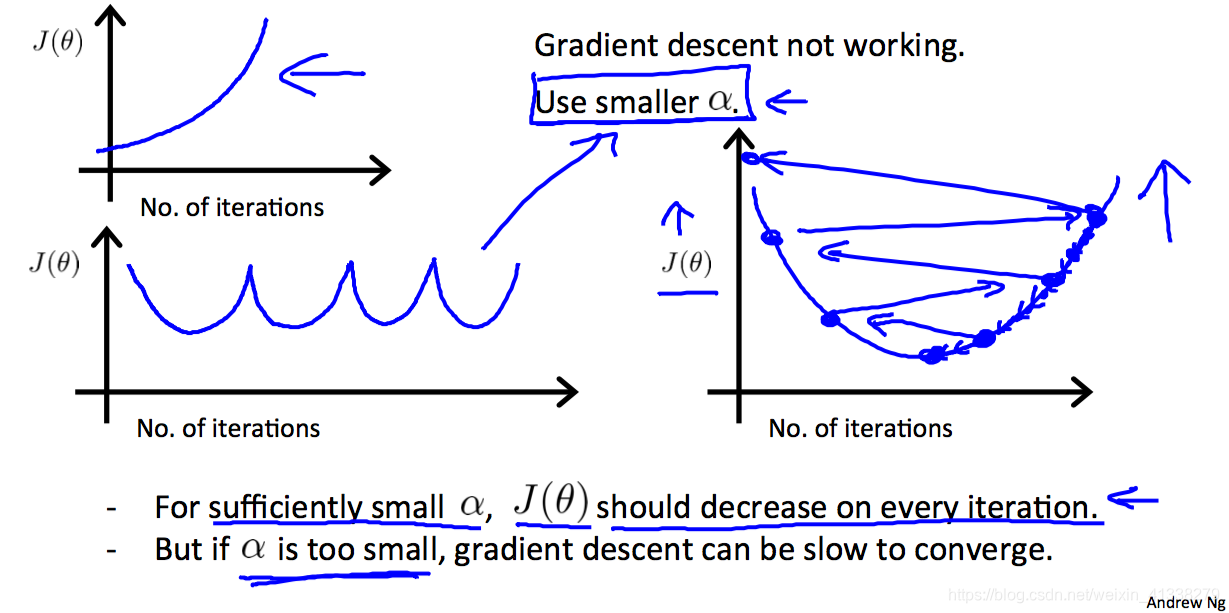
最后一种情况则是learning rate的值取值过小,也称之为baby step,虽然gradient descent是work的,但是收敛的速度明显可以通过加大learning rate来实现。
2)how to choose appropriate value for learning rate?
既然通过上面介绍的那个图可以看出learning rate选择的是否合适,那到底应该如何确定一个最合适的值呢?Andrew老师给出的建议是try and see:让learning rate从0.001开始取值,然后每次翻3倍,翻到1甚至更大,然后在每一个取值下观察cost function随着迭代次数的变化趋势,最后找到最适合的那个值就ok啦!
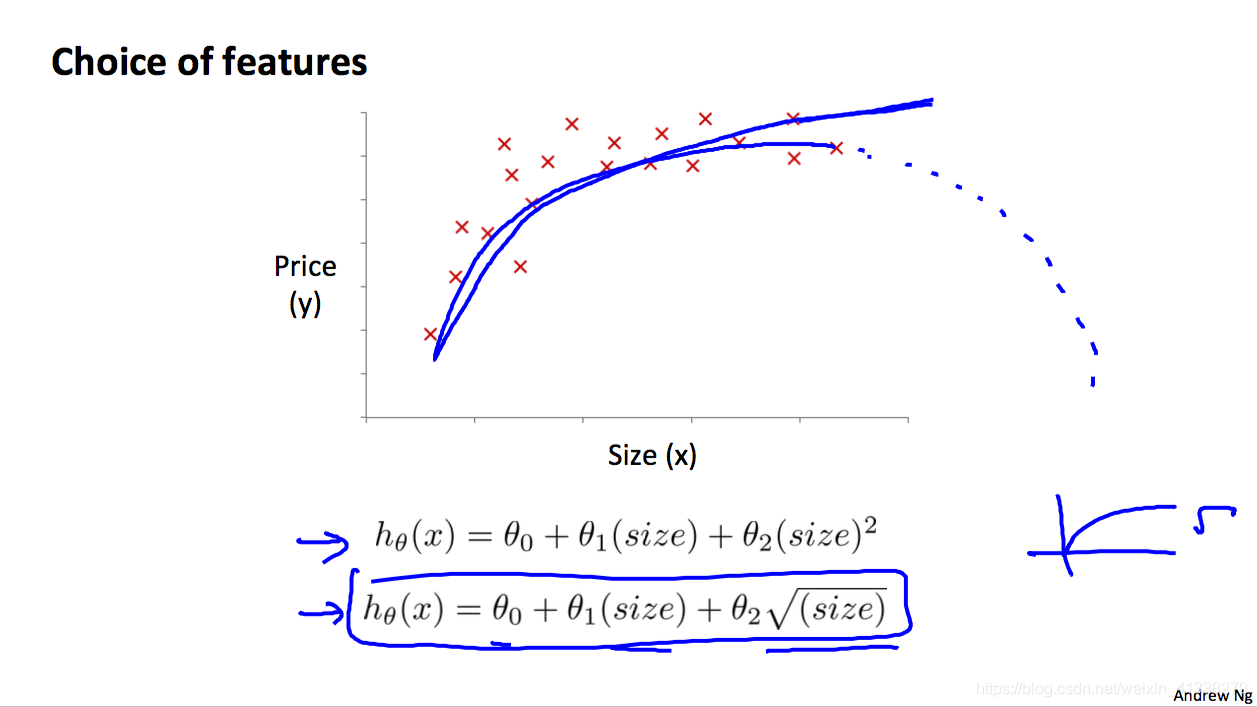
Features and polynomial regression
这是对linear regression拟合的一个拓展,当线性回归的拟合效果并不能很好的时候。Polynomial regression就是多项式回归,其实就是把特征的二次方、三次方甚至更高次方作为数据集的新特征参与模型的训练,具体选取几次方可以通过绘制特征值与对应输出的散点图,看是用二次方的函数曲线拟合效果会比较好还是其他次方,如1/2,3次方等。除了观察图之外也可以做实验啦,看什么情况下cost function的最小值最小。
Normal equation
用来直接求得参数theta的数学公式。
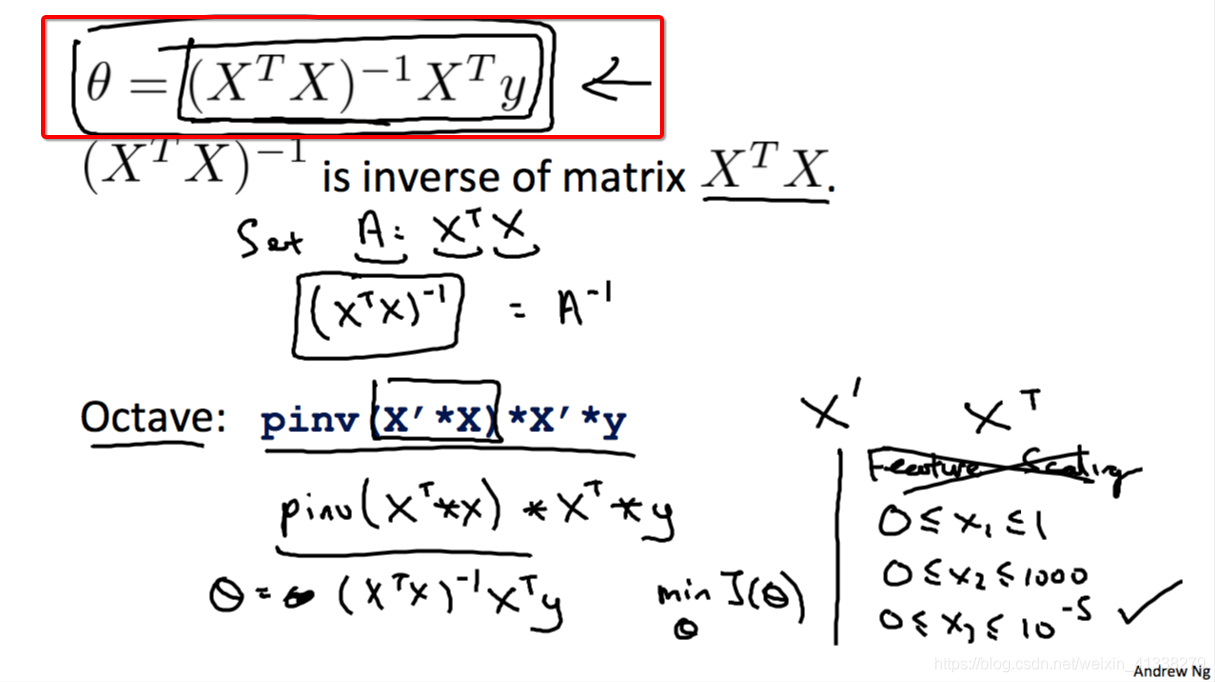
Gradient descent和normal equation之间的比较如下:
|
Gradient decent |
Normal equation |
|
需要给learning rate设置值 |
无需learning rate |
|
需要很多次迭代 |
无需迭代 |
|
当特征数量n很大时,也可以正常工作 |
当特征数量n很大时,计算速度很慢 |
所以可以看出,主要是看训练集输入的规模,也就是特征个数的多少来判断到底是使用gradient decent还是normal equation来得到模型的参数theta。Andrew老师也分享了他自己的经验,当n为10,100,1000,10000这样的数量级时,他会选择用normal equation,因为无需迭代和为learning rate确定合适的值,计算速度也不赖;当到n的数量级到10到6次方这种级别,Andrewa老师则会选择gradient decent而不是要花很长很长时间才能计算出结果的normal equation。

最后分享一道我做了三遍才做对的测试题。
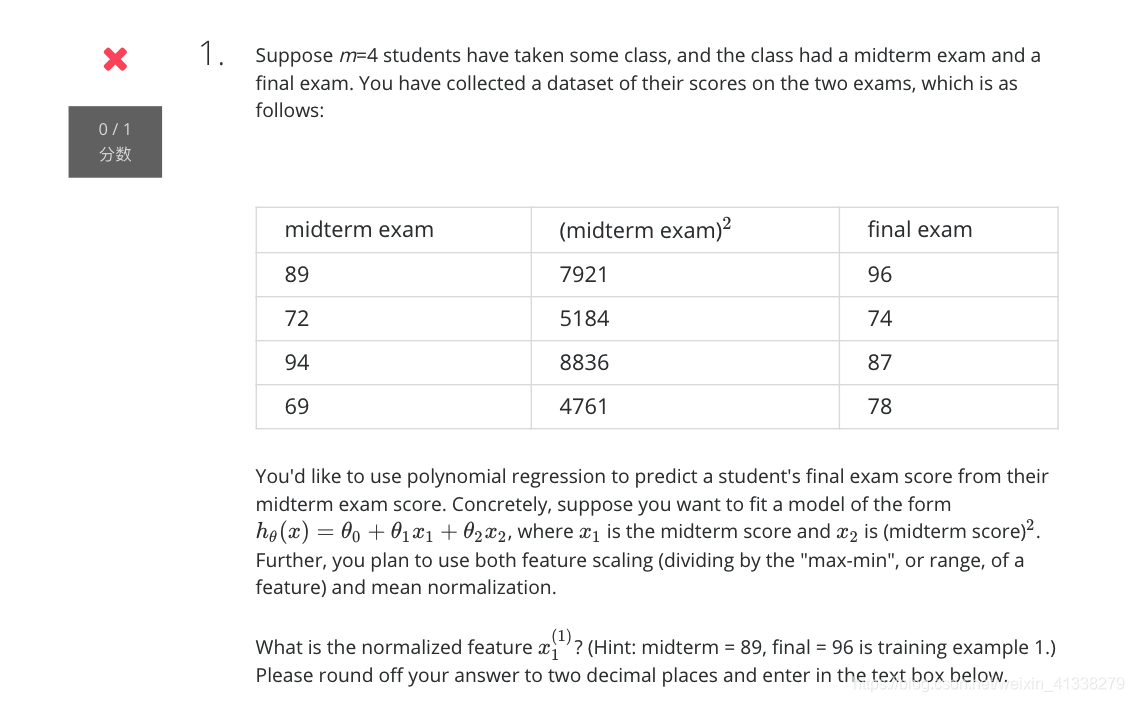
我当时做错的原因是,我认为分数嘛,取值范围不就是0到100吗,所以把max-min设为100。但其实不应该mean normalization公式的分母并不是特征可能的最大值-特征可能的最小值(不要过于主观),而是数据集中该特征的最大值-数据集中该特征的最小值,这一点非常重要!
这道题的计算过程如下:
μ=(89+72+94+69)/4=81
max = 94
min = 69
max - min = 25
the final result is: (89-81)/25=0.28
好啦,今天的分享到这里结束,明天介绍Octave的简单使用!加油?




















 1430
1430

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








