活动调度算法-优快云博客

题目：

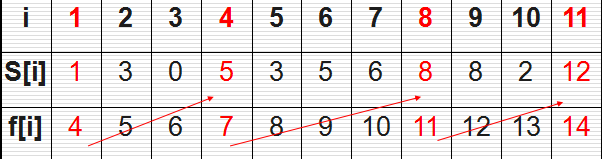
有n个需要在同一天使用同一个教室的活动a1,a2,.....,an,教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi 。一旦被选择后，活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠，ai和aj两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行（最大兼容活动子集）。例如下图所示的活动集合S，其中各项活动按照结束时间单调递增排序。

{a3,a9,a11}是一个兼容的活动子集，但它不是最大子集，因为子集{a1,a4,a8,a11}更大，实际上它是我们这个问题的最大兼容子集，但它不是唯一的一个{a2，a4，a9，a11}

动态规划算法解决思路

我们使用 $s_{ij}$ 代表在活动 $a_{i}$ 结束之后，且 $a_{j}$ 开始之前的那些活动的集合，我们使用c[i,j] 代表 $s_{ij}$ 的最大兼容子集的大小，对上述问题就是求 c[0,12]的解。

a, 当 i > j 或者 $s_{ij}$ 中没有任何活动元素的时候， c[i,j] = 0;

a, 当 i < j

$s_{ij}$ 不存在活动 c[i,j] = 0;

$s_{ij}$ 存在活动的时候，c[i，j] = c[i,t] + c[t,j] + 1 , $a_{t}$ 属于 $s_{ij}$ 中的一个活动（这里是遍历 $s_{ij}$ 集合，然后求得最大兼容子集）

    class Program
    {
        static void Main(string[] args)
        {
            int[] s = { 0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12, 24 };
            int[] f = { 0, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 24 };

            List<int>[,] sij = new List<int>[s.Length,s.Length];

            for (int i = 0; i < s.Length; i++)
            {
                for (int j = 0; j < s.Length; j++)
                {
                    sij[i, j] = new List<int>();
                }
            }
            // j s[j]用来表示第j个活动开始时间
            for (int j = 0; j < s.Length; j++)
            {
                // i f[i]用来表示第 i 个活动结束时间 
                for (int i = 0; i < j; i++)
                {
                    List<int> tmpSij = new List<int>();

                    for (int n = 1; n < s.Length; n++)   //n 第n个活动
                    {
                        if (s[n] >= f[i] && f[n] <= s[j])  //第n个活动开始时间 要大于第i个活动结束时间
                        {
                            tmpSij.Add(n);
                        }
                    } 
                    if (tmpSij.Count > 0)
                    {
                        int maxCount = 0;
                        List<int> tmpList = new List<int>();
                        foreach (int t in tmpSij)
                        {
                            int count = sij[i, t].Count + sij[t, j].Count + 1;    //  存在活动的时候，c[i，j] = c[i,t] + c[t,j] + 1 
                            if (maxCount < count)
                            {
                                maxCount = count;
                                tmpList = sij[i, t].Union<int>(sij[t, j]).ToList<int>();
                                tmpList.Add(t);
                            }
                        }
                        sij[i, j] = tmpList;
                    }
                }
            }

            List<int> l = sij[0, s.Length - 1];
            foreach (int item in l)
            {
               Console.WriteLine("活动：" + item);
            }
            Console.ReadKey();
        }
    }

运行结果

贪心算法

想要使用贪心算法的话，得先找到适合贪心算法的规律（局部最优选择）

对于任何非空的活动集合 S ,假如 $a_{m}$ 是 S 中结束时间最早的活动，则 $a_{m}$ 一定在 S 的某个最大兼容子集中。（如何证明上面结论？反证法）

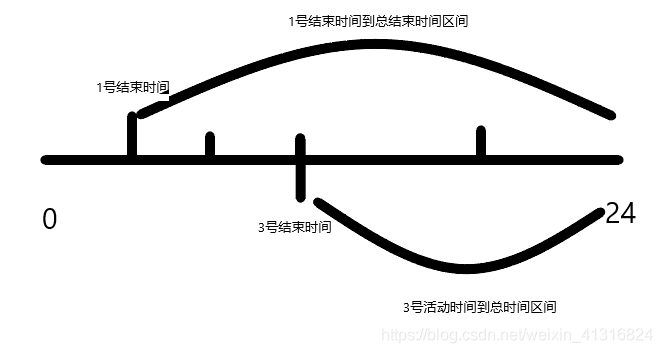
假设活动 1 在最大兼容子集中，那么就存在最大兼容子集 =1号活动 + （1号活动结束的时间到总的结束时间之间的活动子集）

假设活动 3 在最大兼容子集中，那么就存在最大兼容子集 =3号活动 + （3号活动结束的时间到总的结束时间之间的活动子集）

1号活动结束的时间到总的结束时间区间 > 3号活动结束的时间到总的结束时间区间

所以 $a_{m}$ 是 S 中结束时间最早的活动，则 $a_{m}$ 一定在 S 的某个最大兼容子集中。

递归解决

  class Program
    {

        static int[] s = { 0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12, 24 };
        static int[] f = { 0, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 24 };
        static void Main(string[] args)
        {
            List<int> result = Activity(1,s.Length - 1,0,24);
            foreach (var item in result)
            {
                Console.Write(item + " ");
            }

            Console.ReadKey();
        }
        /// <summary>
        /// 
        /// </summary>
        /// <param name="startActivity"> 开始活动编号 </param>
        /// <param name="endActivity"> 结束活动编号 </param>
        /// <param name="startTime"> 开始时间 </param>
        /// <param name="endTime"> 结束时间 </param>
        /// <returns></returns>
        static List<int> Activity(int startActivity, int endActivity, int startTime, int endTime)
        {
            // 当开始活动序号 > 结束活动序号 说明以及不存在可递归的活动了 或者 开始时间 >= 结束时间 没有时间进行活动了
            if (startActivity > endActivity || startTime >= endTime)
            {
                return new List<int>();
            }

            List<int> tmp = new List<int>();
            int tmpActivity = startActivity;
            for (int i = startActivity; i <= endActivity; i++)
            {
                if (s[i] >= startTime && f[i] < endTime)
                {
                    tmpActivity = i;
                    tmp.Add(i);
                    break;
                }
            }
            return tmp.Union<int>(Activity(tmpActivity + 1, endActivity, f[tmpActivity], endTime)).ToList<int>();
        }
    }

运行结果：

迭代解决

    class Program
    {
        static void Main(string[] args)
        {
            
            int[] s = { 0, 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12, 24 };
            int[] f = { 0, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 24 };

            int startTime = 0;
            int endTime = 24;
            int startActivity = 1;
            List<int> resultList = new List<int>();
            for (int i = startActivity; i < s.Length; i++)
            {
                if (s[i] >= startTime && f[i] < endTime)
                {
                    startTime = f[i];
                    resultList.Add(i);
                }
            }

            foreach (var item in resultList)
            {
                Console.Write(item + " ");
            }

            Console.ReadKey();
        }
    }

活动选择问题