本文详细解析了标准差和协方差的概念，通过实例说明标准差如何衡量数据的散布度，以及协方差如何度量两个随机变量之间的关系。深入浅出，帮助读者更好地理解统计学中的关键概念。
【1】标准差给我们描述的则是样本集合的各个样本点到均值的距离之平均。
例子：以这两个集合为例，[0，8，12，20]和[8，9，11，12]，两个集合的均值都是10，但显然两个集合差别是很大的，计算两者的标准差，前者是8.3，后者是1.8，显然后者较为集中，故其标准差小一些，标准差描述的就是这种“散布度”。
之所以除以n-1而不是除以n，是因为这样能使我们以较小的样本集更好的逼近总体的标准差，即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。
【2】协方差就是这样一种用来度量两个随机变量关系的统计量
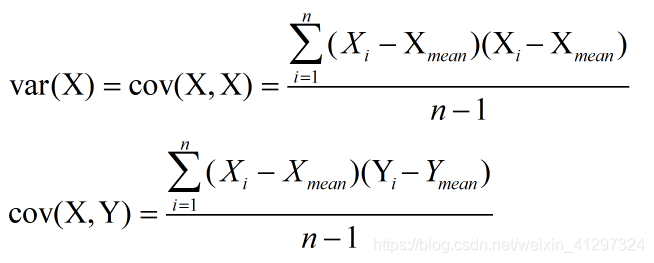
多个协方差就可以构成协方差矩阵
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
