Berkeley CS61B Spring 2019 打卡(2)

刷题记录在Dropbox Paper上

2019 June 25 || Subtype Polymorphism vs. HoFs

• Subtype Polymorphism vs. HoFs

1. Dynamic Method Selection Puzzle
2. Subtype Polymorphism vs. Explicit HoFs
3. Application 1: Comparables
4. Application 2: Comparators

• Casting is just a trick for compiler; It DOESN’T do any practical thing.
• Polymorphism: “providing a single interface to entities of different types”
• Using built-in Comparable interface And compareTo has many implementations such as for Strings.

    public interface Comparable<T> {
         public int compareTo(T obj);
    } 

• For comparison under different criteria, use Comparator interface. It is built on Comparable interface and its compareTo method.

import java.util.Comparator;
public interface Comparator<T> {
	int compare(T o1, T o2);
}

• Interfaces provide us with the ability to make callbacks:

1. Sometimes a function needs the help of another function that might not have been written yet.
   < Example: max needs compareTo
   < The helping function is sometimes called a “callback”.
2. Some languages handle this using explicit function passing.
3. In Java, we do this by wrapping up the needed function in an interface (e.g. Arrays.sort < needs compare which lives inside the comparator interface)
4. Arrays.sort “calls back” whenever it needs a comparison.
   < Similar to giving your number to someone if they need information.
   < See Project 1B to explore how to write code that uses comparators.

2019 June 26 || Lists and Sets in Java

• Primitive type cannot be dereferenced! (cannot be treated as an ordinary Object)
  Thus,

1. .equals(Object) cannot be used to the primitive types. AND it is not usable for user-defined classes, so we need to override the default equals() method.
2. You should use the according non-primitive types, like using Integer for int.

• Any class in java is derived from Object class.

• Generic type variable / Actual type variable
  

• Exceptions: Something breaks the control flow of java.

1. Implicit exceptions:
   ex. Exception in thread "main" java.lang.NullPointerException
2. Explicit exceptions: (our own exceptions)
   ex. throw new IllegalArgumentException("Cannot add null!"); which we can use catch later.

• throw some exceptions crash the codes, instead we need to do something to avoid the exceptions.
  Ex. (To avoid NullPointerException)

1. Ignore nulls. (return if Null is detected.)
2. Fix contains so that it doesn’t crash if items[i] is null. (For this, we should use “==” instead of .equals() for Null.)

• Enhanced for loop
  for (int i : javaset){}

• Iteration
  To support the enhanced for loop:

1. Add an iterator() method to your class that returns an Iterator.
2. The Iterator returned should have a useful hasNext() and next() method.
3. Add implements Iterable to the line defining your class.

• Added a toString() method.
  Beware of String concatenation.

• Added an equals(Object) method.
  Make sure to deal with null and non-ArraySet arguments!
  Used getClass to check the class of the passed object. Use sparingly.

• For every Object class we need to know weather our method should override the existing method for Object class!

• Iterable<T> listOfItems;
String.join(",",listOfItems);

• Variable Arguments (Varargs) : here a is implicitly declared as an array of the type.

public static <Glerp> ArraySet<Glerp> of(Glerp... stuff){
	ArraySet<Glerp> returnSet = new ArraySet<Glerp>();
	for(Glerp x : stuff){
		returnSet.add(x);
	}
	return returnSet;
}

2019 June 27 || Asymptotics I

• To characterize the order of growth
• Big O (equals or more than (Upper Bound))
  
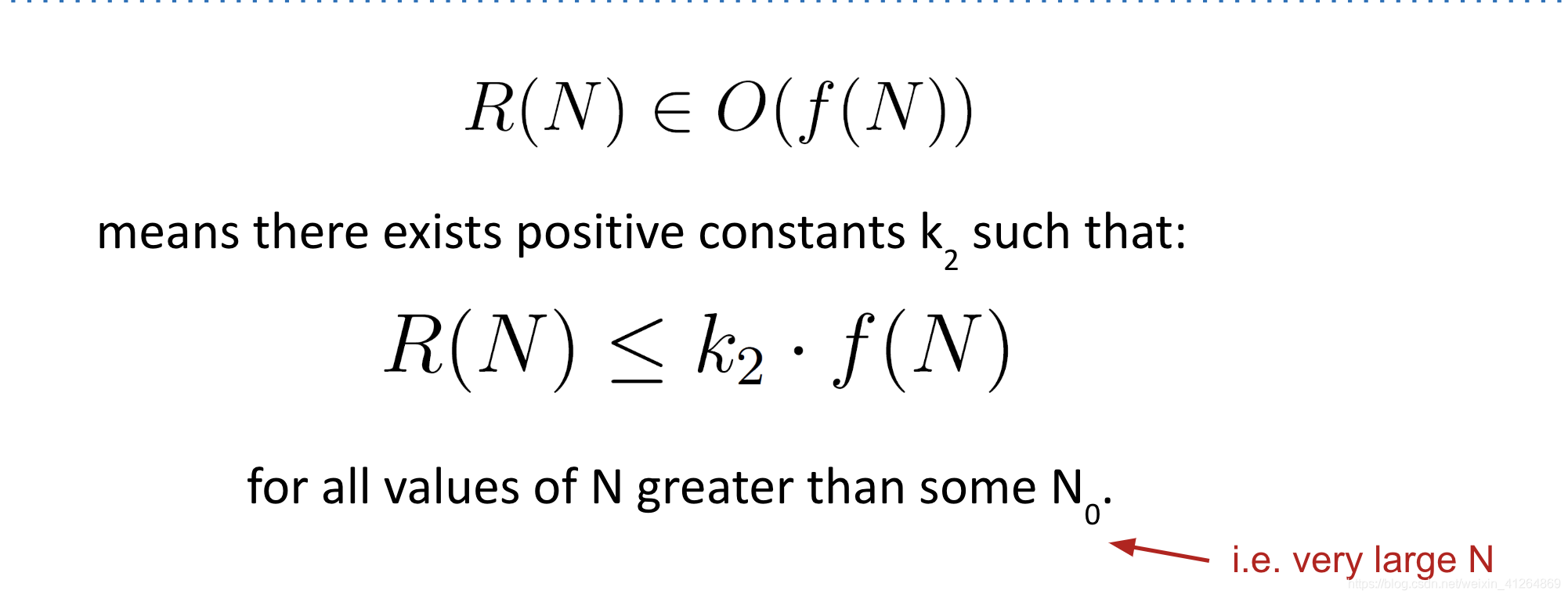
• Big Theta (equals)
  

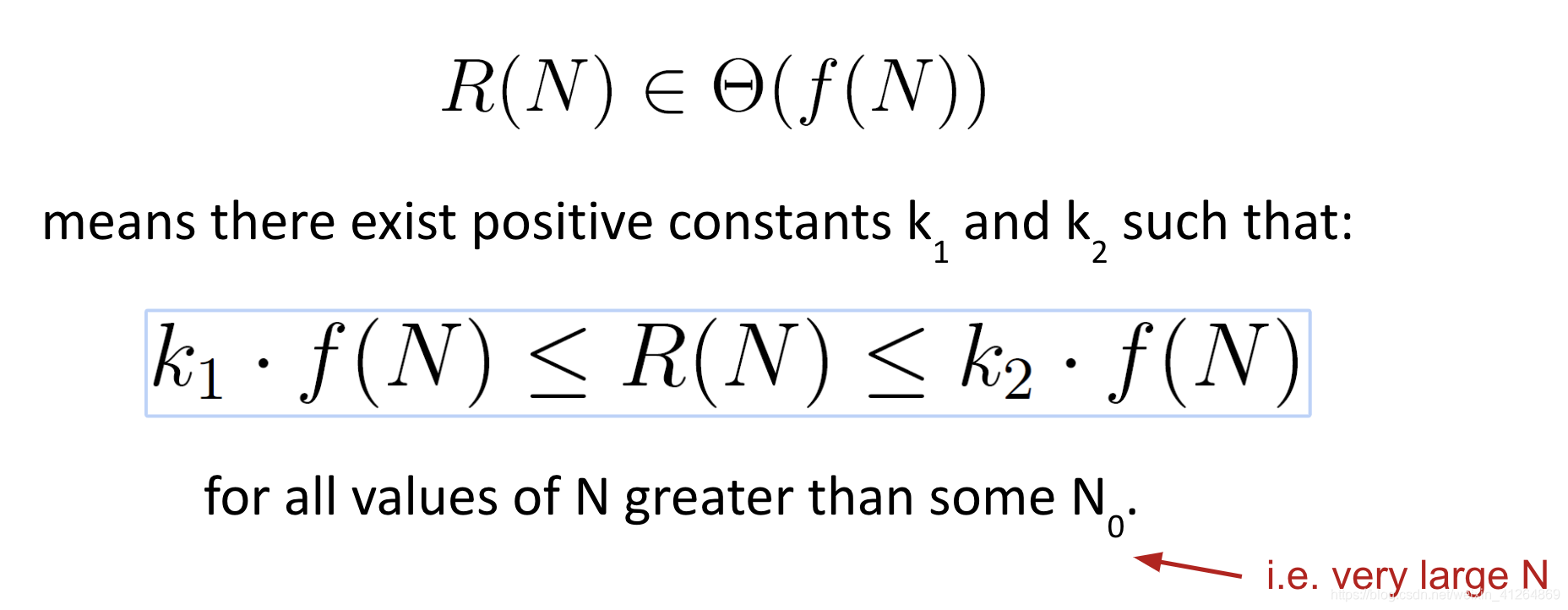
2019 June 27 || Disjoint Sets

• The ideas that made our implementation efficient:

  • Represent sets as connected components (don’t track individual connections).
    • ListOfSetsDS: Store connected components as a List of Sets (slow, complicated).
    • QuickFindDS: Store connected components as set ids.
    • QuickUnionDS: Store connected components as parent ids.
      • WeightedQuickUnionDS: Also track the size of each set, and use size to decide on new tree root.
        • WeightedQuickUnionWithPathCompressionDS: On calls to connect and isConnected, set parent id to the root for all items seen.

• Complexity
  

2019 June 28 || Asymptotics II

• Theoretical analysis of algorithm performance requires careful thought.

  • There are no magic shortcuts for analyzing code.
  • In our course, it’s OK to do exact counting or intuitive analysis.
    • Know how to sum 1 + 2 + 3 … + N and 1 + 2 + 4 + … + N.
    • We won’t be writing mathematical proofs in this class.
  • Many runtime problems you’ll do in this class resemble one of the five problems from today. See textbook, study guide, and discussion for more practice.
    This topic has one of the highest skill ceilings of all topics in the course.

• Different solutions to the same problem, e.g. sorting, may have different runtimes.

  • N^2 vs. N log N is an enormous difference.
  • Going from N log N to N is nice, but not a radical change.

2019 June 28 || ADTs, Sets, Maps, BSTs

• Abstract data types (ADTs) are defined in terms of operations, not implementation.

  • Several useful ADTs: Disjoint Sets, Map, Set, List.
  • Java provides Map, Set, List interfaces, along with several implementations.

• We’ve seen two ways to implement a Set (or Map): ArraySet and using a BST.

  • ArraySet: Θ(N) operations in the worst case.
  • BST: Θ(log N) operations if tree is balanced.

• BST Implementations:

  • Search and insert are straightforward (but insert is a little tricky).
  • Deletion is more challenging. Typical approach is “Hibbard deletion”.

2019 June 29 || B-Trees

• BSTs have best case height Θ(log N), and worst case height Θ(N).

  • Big O is not the same thing as worst case!

• B-Trees are a modification of the binary search tree that avoids Θ(N) worst case.

  • Nodes may contain between 1 and L items.
  • contains works almost exactly like a normal BST.
  • add works by adding items to existing leaf nodes.
    • If nodes are too full, they split.
  • Resulting tree has perfect balance. Runtime for operations is O(log N).
  • Have not discussed deletion. See extra slides if you’re curious.
  • Have not discussed how splitting works if L > 3 (see some other class).
  • B-trees are more complex, but they can efficiently handle ANY insertion order.

• The deletion of B tree contains 3 conditions

https://docs.google.com/presentation/d/1zhQDvbcDZ9RJgJl0bmqwFFlHP8ExbDFo36Q9ZWH9EgU/edit#slide=id.g508ece10b0_1_1228

2019 June 29 || Red Black Trees

• Left-Leaning Red Black Binary Search Tree (LLRB) Properties

  • Some handy LLRB properties:
    • No node has two red links [otherwise it’d be analogous to a 4 node, which are disallowed in 2-3 trees].
    • Every path from root to a leaf has same number of black links [because 2-3 trees have the same number of links to every leaf]. LLRBs are therefore balanced.

• LLRB Construction general rules

  • Insert as usual into a BST.
  • Use zero or more rotations to maintain the 1-1 mapping.

• LLRB Construction detailed rules

  • When inserting: Use a red link.

  • If there is a right leaning “3-node”, we have a Left Leaning Violation.
    Rotate left the appropriate node to fix.

  • If there are two consecutive left links, we have an Incorrect 4 Node Violation.
    Rotate right the appropriate node to fix.

  • If there are any nodes with two red children, we have a Temporary 4 Node.
    Color flip the node to emulate the split operation.

  • It is possible that a rotation or flip operation will cause an additional violation that needs fixing.

• LLRB Runtime

  • The runtime analysis for LLRBs is simple if you trust the 2-3 tree runtime.

    • LLRB tree has height O(log N).
    • Contains is trivially O(log N).
    • Insert is O(log N).
      • O(log N) to add the new node.
      • O(log N) rotation and color flip operations per insert.

  • We will not discuss LLRB delete.

    • Not too terrible really, but it’s just not interesting enough to cover. See optional textbook if you’re curious (though they gloss over it, too).

2019 June 29 || Hashing

2019 June 30 || Heaps and PQs

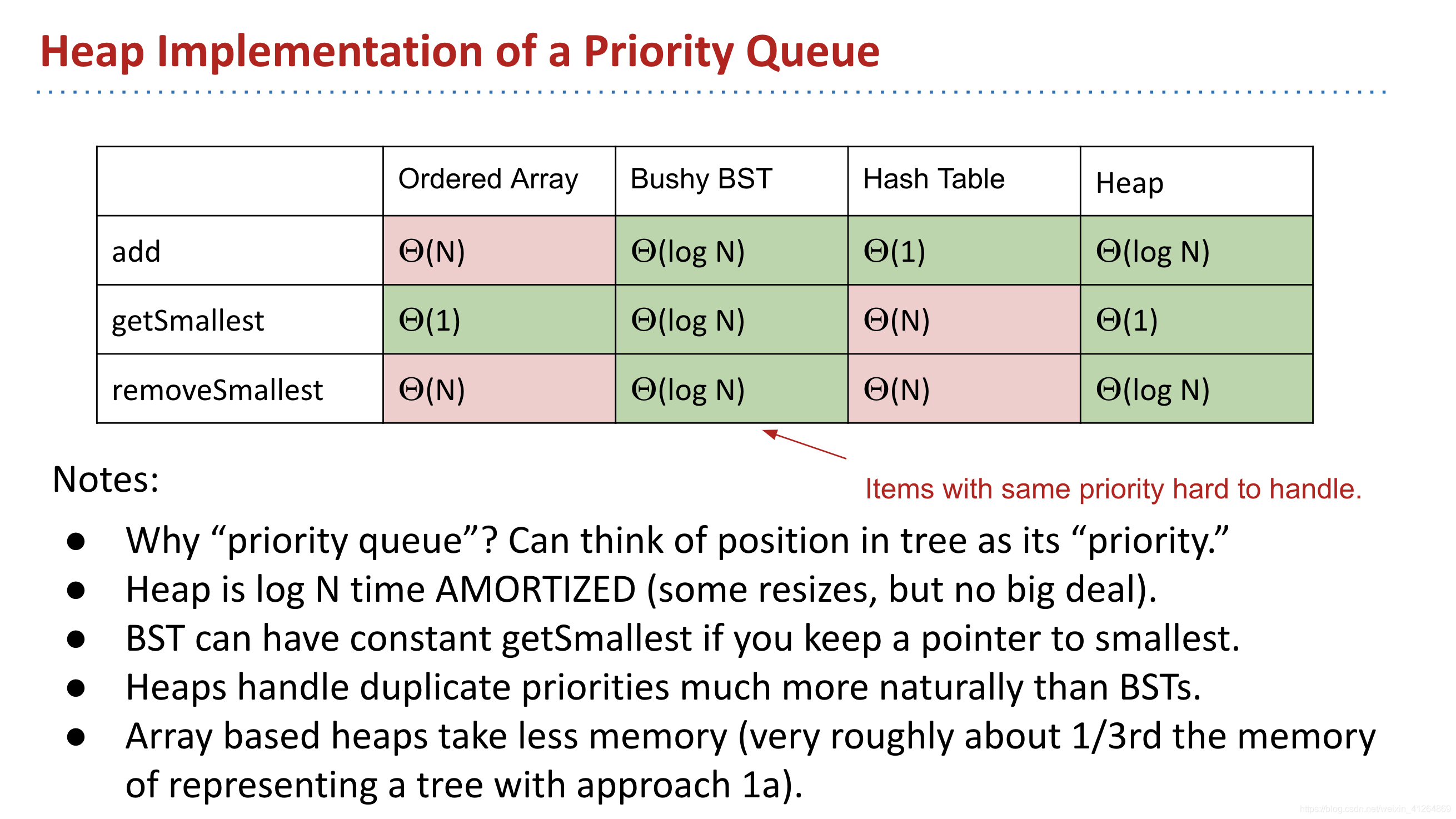
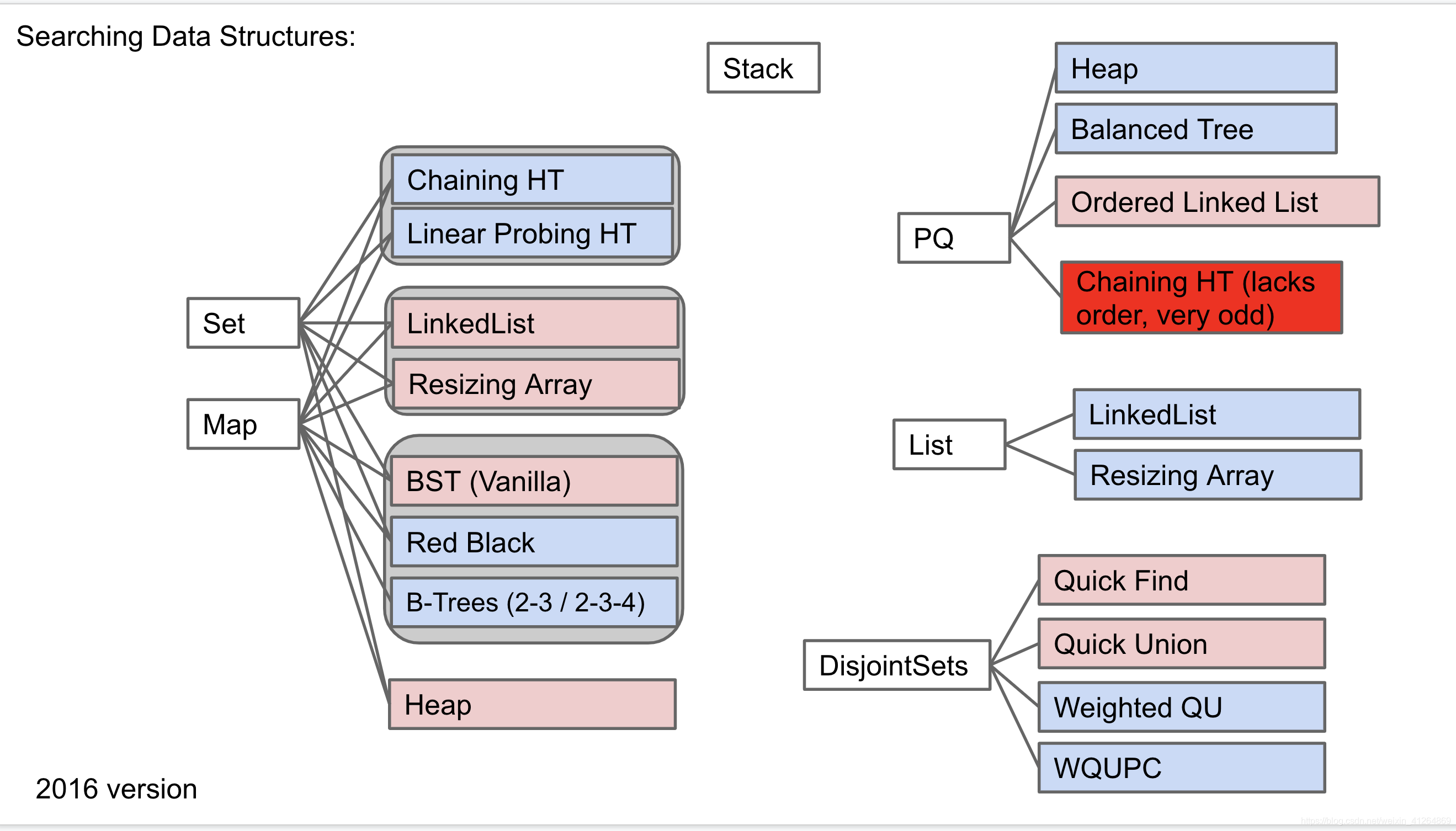
2019 July 1 || Prefix Operations and Tries

• Comparable and Comparator

// Comparable
public class Employee implements Comparable<Employee> {
public int compareTo(Employee emp) {

// Comparator
public class EmployeeComparatorByIdAndName implements Comparator<Employee> {
    @Override
    public int compare(Employee o1, Employee o2) {