排列数

最新推荐文章于 2019-09-12 10:47:42 发布

原创最新推荐文章于 2019-09-12 10:47:42 发布 · 1.6k 阅读

0 ·

CC 4.0 BY-SA版权

组合数学专栏收录该内容

11 篇文章

订阅专栏

do{
}while(next_permutation(a+1,a+n+1));
//a[]数组一定要是已经从小到大排序好的,才能遍历全排列

排列组合常用公式:

（1）证明 0!=1；

（2）证明 C(n,m)=C(n,n-m)；

（3）证明 C(n+1,m)=C(n,m)+C(n,m-1)；

（4）证明 C(n,r)+C(n,r+1)=C(n+1,r+1)；

（5）证明 C(n,0)+C(n,1)+C(n,2)+...+C(n,n)=2^n

A(n,m) = N!/(n-m)!，C(n,m)=N!/((n-m)!*m!)

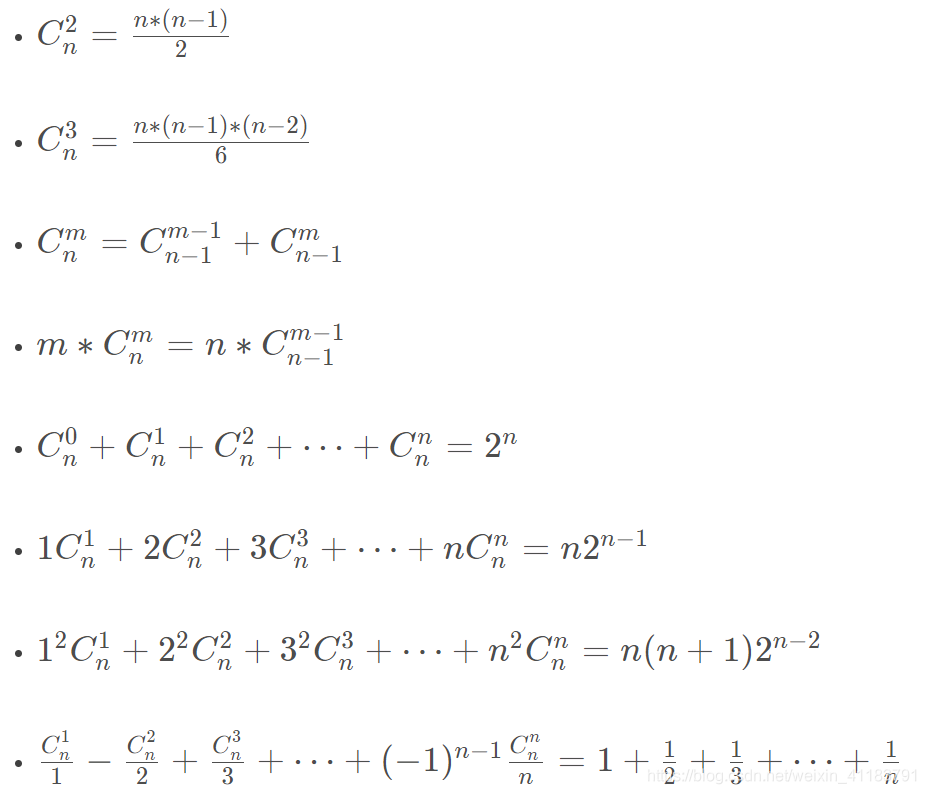
排列组合打表:

ll C[MAXN][MAXN];//组合数

void init(int n)
{
    C[0][0]=1;
    for(int i=1;i<=n;i++)
    {
        C[i][0]=1;
        for(int j=1;j<=i;j++)
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
    }
}

求比较大的排列组合:

1费马小定理求逆元，

2预处理一个n！的数组，

3为了防止乘法，乘方爆long long int ，采用了快速乘法和快速幂

#include<bits/stdc++.h>
#define ll long long
#define mod (ll)(1e9+7)
using namespace std;
ll a[100005];
ll Pow(ll a,ll b){
    a%=mod;
    ll ans = 1;
    while(b)
    {
        if(b&1)
            ans = (ans*a)%mod;
        a = (a*a)%mod;
        b/=2;
    }
    return ans%mod;
}
ll Quk(ll a,ll b){
    a%=mod;
    ll ans = 0;
    while(b)
    {
        if(b&1)
            ans = (ans+a)%mod;
        a = (a+a)%mod;
        b/=2;
    }
    return ans%mod;
}
ll C(ll n,ll m){
    return Quk(Quk(a[n],Pow(a[n-m],mod-2)),Pow(a[m],mod-2))%mod;
}
ll A(ll n,ll m){
    return Quk(a[n],Pow(a[n-m],mod-2))%mod;
}
int main()
{
    a[0]=a[1]=1;
    for(ll i=2;i<=100000;i++)
        a[i]=Quk(a[i-1],i);
    ll n,m;
    while(~scanf("%lld%lld",&n,&m))
        printf("%lld\n",C(n,m));
    return 0;
}

例题1:

https://ac.nowcoder.com/acm/problem/18203

解析:

对于每个数字在长度为 k 的子序列中出现的次数为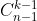 $C_{n-1}^{k-1}$ 次

对于 ai这个数来说，如果它出现在子序列中，在剩下n-1个数中在选k-1个数入序列所以结果为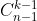 $C_{n-1}^{k-1}$ .
如果 ai这个数字需要计入结果中，那么 ai一定不是最大值或者最小值，所以我们从反面考虑：
1) 假设 ai 是最大值的情况,我们把ai排序,遍历,如果ai是最大值

我们只需要从前 i 个数中选取 k−1个数即可，方法数为 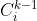$C_{i}^{k-1}$ (前i个选k-1个入序列和最大的数组成序列,需要去掉)
2) 同理，ai 是最小值的情况的方法数为 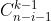$C_{n-i-1}^{k-1}$
综上，令 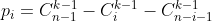$p_i= C_{n-1}^{k-1}-C_{i}^{k-1}-C_{n-i-1}^{k-1}$ 对于 ai这个数来说，它对答案的贡献为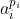 $a_i^{p_i}$
最终的答案为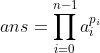： $ans=\prod_{i=0}^{n-1}a_i^{p_i}$
最后，只需要预处理组合数取模即可。

1e9+7是素数,其phi为1e9+6

ac:

#include <bits/stdc++.h>
#define ll long long
#define mod 1000000007
#define N 1005
using namespace std;
ll c[N][N];

ll poww(ll a,ll b){
    ll ans = 1;
    while(b){
        if(b&1){
            ans = (ans*a)%mod;
        }
        b>>=1;
        a = (a*a)%mod;
    }
    return ans;
}

void init()//组合数预处理
{
    c[0][0] = 1;
    for(int i=0;i<=1000;++i){
        for(int j=0;j<=i;++j){
            if(j==0||i==j){
                c[i][j] = 1;
            }else{
                c[i][j] = (c[i-1][j]+c[i-1][j-1])%(mod-1);//mod的欧拉值为(mod-1)
            }
        }
    }
}

int t,n,m;
ll a[N];
int main()//1e9+7是素数,其phi为1e9+6
{
    scanf("%d",&t);
    init();
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        sort(a,a+n);
        ll sum = 1;
        for(int i=0;i<n;i++)
        {
            ll tmp = c[n-1][m-1];
            tmp = (tmp-c[n-i-1][m-1]+mod-1)%(mod-1);
            tmp = (tmp - c[i][m-1] + mod-1)%(mod-1);
            sum = sum*poww(a[i],tmp)%mod;
        }
        printf("%lld\n",sum);
    }
    return 0;
}

例题2:

subsequence 1

题意:

给定s串和t串,求s串中子序列组成的串字典序大于t串的数目

解析:

字典序大于s串的情况有两种:1.长度大于s(不能有前导零),2.长度等于s 分别计算

1.对于长度大于s的

C(n,m)-所以包含前导零的子序列:

for(int i=1;i<=n;i++){
    if(s[i]=='0'){
        for(int j=m;j<=n-1;j++)
            ans=(ans-C[n-i][j]+mod)%mod;
    }
}

以非零开头的所以子序列:

for(int i=1;i<=n;i++){
    if(s[i]=='0')
        continue;
    for(int j=m;j<=n-i;j++)
        ans=(ans+C[n-i][j])%mod;
}

2.长度等于s的串:

设dp[i][j]:在s串的钱i个字符里,选出的子序列和t串匹配了j个字符的种类数

首先dp[i][j]=dp[i-1][j](不选t[i])

如果s[i]==t[j],呢么要加上:dp[i-1][j-1](选t[i])

如果s[i]>t[j]:呢么s[i]后面的所以子序列随便选m-j个都符合要求,i之前取j-1个的种类数*i之后取m-j个的情况种类数

ans+=dp[i-1][j-1]*C[n-i][m-j];

ac:

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 3e3+10;
const ll mod = 998244353;
ll dp[N][N],ans,C[N][N];
char s[N],t[N];
int n,m;
//dp[i][j]:在s串的钱i个字符里,选出的子序列和t串匹配了j个字符的种类数
void init()
{
    C[0][0]=1;
    for(int i=1;i<=N-10;i++)
    {
        C[i][0]=1;
        for(int j=1;j<=i;j++)
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
    }
}

int main(void)
{
    int T;
    scanf("%d",&T);
    init();
    while(T--)
    {
        scanf("%d%d%s%s",&n,&m,s+1,t+1);
        ans=0;
        for(int i=0;i<=n;i++)//初始化，选出0位数的序列数肯定为1
            dp[i][0]=1;

        for(int i=1;i<=n;i++)//计算子序列长为m
        {
            for(int j=1;j<=i&&j<=m;j++)
            {
                dp[i][j]=dp[i-1][j];//继承前面的匹配数,先不选的情况下
                if(s[i]==t[j])//如果s[i]==t[j],呢么种类有已经匹配(前i-1匹配j个(不选第i个))+(前i-1匹配j-1个(选择第i个))
                    dp[i][j]=(dp[i][j]+dp[i-1][j-1])%mod;
                if(s[i]>t[j])//如果s[i]>t[j],呢么在已选i的情况下,后面随便选m-j个,都是符合要求的自选,所以后面答案+前面匹配种类数*后面可以选择数
                    ans=(ans+dp[i-1][j-1]*C[n-i][m-j])%mod;
            }
        }
        for(int i=1;i<=n;i++){
            if(s[i]=='0')
                continue;
            for(int j=m;j<=n-i;j++)
                ans=(ans+C[n-i][j])%mod;
        }
        /*
        for(int i=m+1;i<=n;i++)
            ans=(ans+=C[n][i])%mod;
        for(int i=1;i<=n;i++){
            if(s[i]=='0'){
                for(int j=m;j<=n-1;j++)
                    ans=(ans-C[n-i][j]+mod)%mod;
            }
        }
        */
        printf("%lld\n",ans);
    }
    return 0;
}

康拓展开:

https://blog.youkuaiyun.com/weixin_41183791/article/details/86618778