八大排序算法的小总结

@toc(

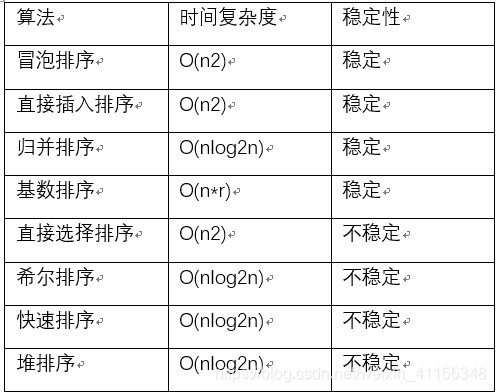
主要的排序算法有以下8种

冒泡排序

算法思路：
遍历数组，把每次遍历数组中最大的那个数移到最后，这个数字以后就不用遍历了，遍历的方法主要从0开始与后一位的数字比较大小，如果前面的数比后面的数大，就交换位置，时间复杂度O(n2)
代码如下：

public static void bubbleSort(int[] arr){
	    for (int i = 0; i < arr.length; i++) {
			for (int j = 0; j < arr.length-i-1; j++) {
				if(arr[j]>arr[j+1]) {
					swap(arra, j, j+1
				}
			}
		}
	}

直接插入排序

算法思路：遍历数组，把遍历到的每个数字插到前面（前面已经排好序）应该在的位置，通过不断与前面的数字比较大小，如果比前面的数字小，就与前面的数字交换，直到比前面的数字大为止，复杂度O(n2)。

    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
                swap(arr, j, j + 1);
            }
        }
    }

归并排序

算法思路：分冶思想，把数组分成两半进行排序，，等这两半排序好后，需要分配额外的空间new一个数组来把这两半的数组组合起来，组合过程中进行排序，时间复杂度O(nlog2n)。

    public static void mergeSort(int[] arr) {
       if ( arr == null || arr.length < 2 ) {
           return;
       }
       mergeSort(arr, 0, arr.length - 1 ) ;
   }

   public static void mergeSort(int[] arr, int l, int r) {
       if (l == r) {
           return;
       }
       int mid = l + ((r - l) >> 1);
       mergeSort(arr, l, mid);
       mergeSort(arr, mid + 1, r);
       merge(arr, l, mid, r);
   } 

   public static void merge(int[] arr, int l, int m, int r) {
       int[] help = new int[r - l + 1];
       int i = 0;
       int p1 = l;
       int p2 = m + 1;
       while (p1 <= m && p2 <= r) {
           help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
       }
       while (p1 <= m) {
           help[i++] = arr[p1++];
       }
       while (p2 <= r) {
           help[i++] = arr[p2++];
       }
       for (i = 0; i < help.length; i++) {
           arr[l + i] = help[i];
       }
   }

基数排序

算法思路：分别建立10个桶0，1，2，3，4，5，6，7，8，9。然后遍历数组中数字，然后把数字放在与个位数对应的桶中，把数字从桶中拿出来，然后再把数字放在与十位数对应的桶中，然后把数字从桶中拿出来…遍历次数为数组中最大的数的位数（r），时间复杂O(n*r)

public static void radixSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        radixSort(arr, 0, arr.length - 1, maxbits(arr));
    }

    public static int maxbits(int[] arr) {
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            max = Math.max(max, arr[i]);
        }
        int res = 0;
        while (max != 0) {
            res++;
            max /= 10;
        }
        return res;
    }

    public static void radixSort(int[] arr, int begin, int end, int digit) {
        final int radix = 10;
        int i = 0, j = 0;
        int[] count = new int[radix];
        int[] bucket = new int[end - begin + 1];
        for (int d = 1; d <= digit; d++) {
            for (i = 0; i < radix; i++) {
                count[i] = 0;
            }
            for (i = begin; i <= end; i++) {
                j = getDigit(arr[i], d);
                count[j]++;
            }
            for (i = 1; i < radix; i++) {
                count[i] = count[i] + count[i - 1];
            }
            for (i = end; i >= begin; i--) {
                j = getDigit(arr[i], d);
                bucket[count[j] - 1] = arr[i];
                count[j]--;
            }
            for (i = begin, j = 0; i <= end; i++, j++) {
                arr[i] = bucket[j];
            }
        }
    }

    public static int getDigit(int x, int d) {
        return ((x / ((int) Math.pow(10, d - 1))) % 10);
}

#直接选择排序
算法思路：遍历数组找到最小的数字，与前面的数字交换，然后继续遍历后面的数字找到最小的与前面的交换，时间复杂度，O(n2)

public static void selectionSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                minIndex = arr[j] < arr[minIndex] ? j : minIndex;
            }
            swap(arr, i, minIndex);
        }
    }

希尔排序

算法思路：选择一个距离dir(一般这个dir取arr.length/2), 位置相隔为dir的元素分为一组，那一共就有dir个小组，每个小组用插入排序进行排序，等所有小组都排好序后，然后dir=dir/2，继续分组，每个小组继续使用插入排序…直到dir<1（dir条件为dir>=1), 算法复杂度O(n2),不稳定;

public static void shellSort(int arr[]) {
      int dir=arr.length/2;
      int x,j,k=1;
      while(dir>=1) {
         for(int i=dir;i<arr.length;i++) {
            x=arr[i];
           j=i-dir;
            //直接插入排序，会向前找所适合的位置
            while(j>=0 && arr[j]>x) {
                //交换位置
                arr[j+dir]=arr[j];
                j=j-dir;
            }
          arr[j+dir]=x;
         }
         dir=dir/2;
      }

快速排序

算法思路：取一个标为通常为数组第一个当作标为，整体思路就是把小于标位的元素凡在数组左边，把大于标位的元素放在数组右边，然后把标位放到中间，是左边的所有元素小于右边的元素，但左右两边的元素是无序的，然后再通过分冶思想，再继续对左右两边的进行快排，算法复杂度O(nlog2n)

void quickSort(int r[ ],int left,int right)
{	int i=left, j=right;
	int x=r[i];
	while (i<j)
	{   while ( (r[j]>=x) && (j>i) )  
                              j=j-1;           
                 r[i]=r[j];                    
	     while ( (r[i]<=x) && (j>i) )
                              i=i+1;         
	     r[j]=r[i]; }              
	r[i]=x;                       
	quicksort(r,left,i-1);  
	quicksort(r,i+1,right); 
}

堆排序

算法思路：一共分为两部分
1，建立大根堆（父节点一定大于子节点）
2，建立完大根堆后，把数组最后一个数（最后一个叶子节点）和数组第一个数(根节点）交换，然后根节点一层一层的下沉又变成叶子节点，整个数组又变成了大根堆，然后继续2步骤，知道所有元素都当过根节点，算法复杂度O(nlong2n)

    public int[] sort(int[] arr ) throws Exception 
        int len = arr.length;
        //建立大根堆
        buildMaxHeap(arr, len);
        for (int i = len - 1; i > 0; i--) {
        //把数组最后一个数（最后一个叶子节点）和数组第一个数(根节点）交换
            swap(arr, 0, i);
            len--;
            //然后根节点一层一层的下沉又变成叶子节点，整个数组又变成了大根堆
            heapify(arr, 0, len);
        }
        return arr;
    }

    private void buildMaxHeap(int[] arr, int len) {
        for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
            heapify(arr, i, len);
        }
    }

    private void heapify(int[] arr, int i, int len) {
        int left = 2 * i + 1;
        int right = 2 * i + 2;
        int largest = i;

        if (left < len && arr[left] > arr[largest]) {
            largest = left;
        }
        if (right < len && arr[right] > arr[largest]) {
            largest = right;
        }
        if (largest != i) {
            swap(arr, i, largest);
            heapify(arr, largest, len);
        }
    }

    private void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }