引言
在高项的第21章,运筹学中有一个相对比较复杂的算法,匈牙利算法,很多机构的老师在这一张的教学中,会告诉我们说这个只会考一分,可以不需要掌握,而经历过2025年第二批的考生就会发现,案例的计算题中居然也出了这道算法题,而我也没太关注这个算法,导致案例题没过,所以今天就和大家一起认认真真学习一下匈牙利算法。
一、什么是匈牙利算法?
匈牙利算法由匈牙利数学家Dénes Kőnig在1931年提出,后来由Harold Kuhn在1955年进一步完善。该算法主要用于解决二分图最大匹配问题,特别是指派问题(Assignment Problem),即在给定的成本矩阵中找到最优的任务分配方案,使得总成本最小(或收益最大)。
适用场景
-
任务分配(如员工与岗位的匹配)
-
资源调度(如出租车与乘客的匹配)
-
图像处理(如目标跟踪中的特征匹配)
二、匈牙利算法的核心思想
匈牙利算法的核心在于调整成本矩阵,通过行归约和列归约来找到最优匹配。其基本步骤如下:
步骤 1:构建成本矩阵
假设我们有4个任务和4个工人,每个工人完成不同任务的成本如下:
| 任务1 | 任务2 | 任务3 | 任务4 | |
| 工人A | 6 | 7 | 11 | 2 |
| 工人B | 4 | 5 | 9 | 8 |
| 工人C | 3 | 1 | 10 | 4 |
| 工人D | 5 | 9 | 8 | 2 |
步骤 2:行归约
对每一行,减去该行的最小值,使得每行至少有一个0:
-
工人A:最小值为2 → 减去2
-
工人B:最小值为4 → 减去4
-
工人C:最小值为1 → 减去1
-
工人D:最小值为2 → 减去2
调整后的矩阵:
| 任务1 | 任务2 | 任务3 | 任务4 | |
| 工人A | 4 | 5 | 9 | 0 |
| 工人B | 0 | 1 | 5 | 4 |
| 工人C | 2 | 0 | 9 | 3 |
| 工人D | 3 | 7 | 6 | 0 |
步骤 3:列归约
对每一列,减去该列的最小值(如果该列还没有0):
-
任务1:最小值已经是0(不调整)
-
任务2:最小值是0(不调整)
-
任务3:最小值是5 → 减去5
-
任务4:最小值是0(不调整)
调整后的矩阵:
| 任务1 | 任务2 | 任务3 | 任务4 | |
| 工人A | 4 | 5 | 4 | 0 |
| 工人B | 0 | 1 | 0 | 4 |
| 工人C | 2 | 0 | 4 | 3 |
| 工人D | 3 | 7 | 1 | 0 |
步骤 4:寻找独立零
尝试用最少的横线或竖线覆盖所有0,如果线条数等于矩阵的阶数(这里是3),如果这个数量大于等于矩阵的行列数,那么直接跳到最后一步,则找到最优解。
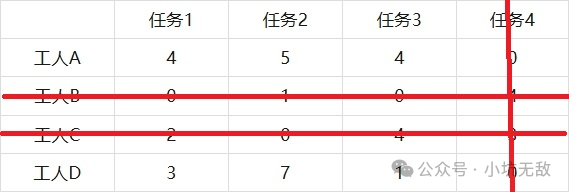
步骤5:剩余矩阵处理
-
剩余矩阵减去矩阵最小值1
-
交点加最小值1
得到矩阵如下
| 任务1 | 任务2 | 任务3 | 任务4 | |
| 工人A | 3 | 4 | 3 | 0 |
| 工人B | 0 | 1 | 0 | 5 |
| 工人C | 2 | 0 | 4 | 4 |
| 工人D | 2 | 6 | 0 | 0 |
重复步骤四直到直线数量等于矩阵行或列
步骤6:得到最优解
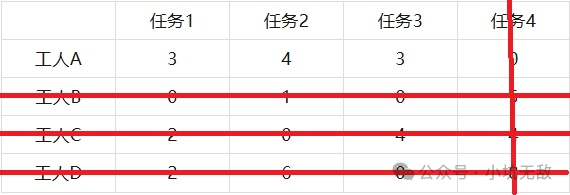
找到当前某行仅有1个0,划掉这个0对应的行列,重复操作直到匹配完成
| 任务1 | 任务2 | 任务3 | 任务4 | |
| 工人A | 3 | 4 | 3 | 0 |
| 工人B | 0 | 1 | 0 | 5 |
| 工人C | 2 | 0 | 4 | 4 |
| 工人D | 2 | 6 | 0 | 0 |
在本例中,我们可以这样匹配:
-
工人A → 任务4
-
工人B → 任务1
-
工人C → 任务2
-
工人D → 任务3
这样,总成本 = 2(A-4) + 4(B-1) +1(C-2) + 8(D-3) = 15
我们就可以很快的计算出了最优解
三、2025年高项案例题
接下来我们看一下2025年案例题
根据作者搜集资料,题目大概就是,我们已知各组完成各项活动的总费用,让我们确保项目能够用最小费用完成,表格如下
| A | B | C | D | E | F | |
| 1组 | 7 | 12 | 13 | 9 | 11 | 10 |
| 2组 | 3 | 11 | 13 | 6 | 6 | 9 |
| 3组 | 3 | 13 | 12 | 8 | 8 | 6 |
| 4组 | 3 | 13 | 11 | 5 | 11 | 10 |
| 5组 | 6 | 14 | 14 | 8 | 6 | 7 |
| 6组 | 3 | 11 | 14 | 5 | 8 | 6 |
按照上面步骤,我们计算一次
步骤 1:行归约
| A | B | C | D | E | F | |
| 1组 | 0 | 5 | 6 | 2 | 4 | 3 |
| 2组 | 0 | 8 | 10 | 3 | 3 | 6 |
| 3组 | 0 | 10 | 9 | 5 | 5 | 3 |
| 4组 | 0 | 10 | 8 | 2 | 8 | 7 |
| 5组 | 0 | 8 | 8 | 2 | 0 | 1 |
| 6组 | 0 | 8 | 11 | 2 | 5 | 3 |
步骤 2:列归约
| A | B | C | D | E | F | |
| 1组 | 0 | 0 | 0 | 0 | 4 | 2 |
| 2组 | 0 | 3 | 4 | 1 | 3 | 5 |
| 3组 | 0 | 5 | 3 | 3 | 5 | 2 |
| 4组 | 0 | 5 | 2 | 0 | 8 | 6 |
| 5组 | 0 | 3 | 2 | 0 | 0 | 0 |
| 6组 | 0 | 3 | 5 | 0 | 5 | 2 |
步骤 3:寻找独立零
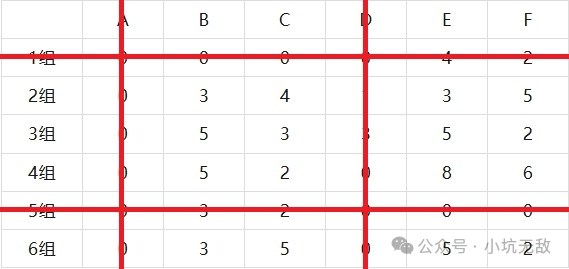
步骤5:剩余矩阵处理
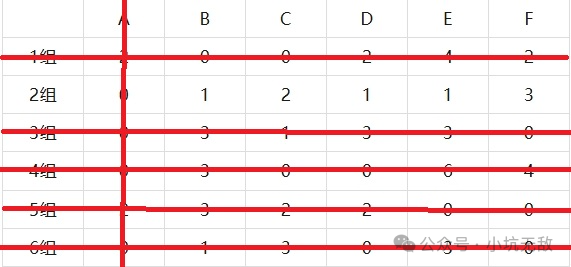
步骤6:得到最优解
| A | B | C | D | E | F | |
| 1组 | 2 | 0 | 0 | 2 | 4 | 2 |
| 2组 | 0 | 1 | 2 | 1 | 1 | 3 |
| 3组 | 0 | 3 | 1 | 3 | 3 | 0 |
| 4组 | 0 | 3 | 0 | 0 | 6 | 4 |
| 5组 | 2 | 3 | 2 | 2 | 0 | 0 |
| 6组 | 0 | 1 | 3 | 0 | 3 | 0 |
最小成本= 12(1组-B) + 3(2组-A) + 6(3组-F) + 11(4组-C) + 6(5组-E) + 5(6组-D) = 43
最后向大家分享下我的学习资料
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








