贪心类型问题

最新推荐文章于 2022-03-10 20:53:16 发布

原创最新推荐文章于 2022-03-10 20:53:16 发布 · 478 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#python #算法 #leetcode

刷题专栏收录该内容

6 篇文章

订阅专栏

本文介绍了贪心算法在解决区间调度、气球引爆、会议室安排和视频剪辑等问题中的应用。通过排序和局部最优选择，实现高效的解决方案，如无重叠区间、最少箭引爆气球、最小会议室数量和视频拼接。同时，讨论了跳跃游戏中的贪心策略，展示如何通过每步最优解更新全局最优解。最后，探讨了在加油站问题中如何利用贪心算法找到可行的路径。

文章目录

前言
1. 贪心算法之区间调度问题
- 435. 无重叠区间（中等）
- 452.用最少数量的箭引爆气球（中等）
2. 扫描线技巧：安排会议室
- 253.会议室 II（中等）
3.剪视频剪出一个贪心算法
- 1024.视频拼接（中等）
4. 如何运用贪心思想玩跳跃游戏
- 55.跳跃游戏（中等）
- 45.跳跃游戏 II（中等）
5. 当老司机学会了贪心算法
- 134.加油站（中等）

前言

贪心算法可以认为是动态规划算法的一个特例，相比动态规划，使用贪心算法需要满足更多的条件（贪心选择性质），但是效率比动态规划要高。

比如说一个算法问题使用暴力解法需要指数级时间，如果能使用动态规划消除重叠子问题，就可以降到多项式级别的时间，如果满足贪心选择性质，那么可以进一步降低时间复杂度，达到线性级别的。

什么是贪心选择性质呢，简单说就是：每一步都做出一个局部最优的选择，最终的结果就是全局最优。注意哦，这是一种特殊性质，其实只有一部分问题拥有这个性质。

1. 贪心算法之区间调度问题

435. 无重叠区间（中等）

在这里插入图片描述
方法一
首先看看动态规划的思路
需要移除的数量就是总数量减去不重合的区间个数，这题可以看成一个子序列问题，只不过每个序列中的元素包含起点和终点
首先按起点从小到大排序
状态：当前的序列是从开头到以 i 结尾
选择：前一个选择的interval是哪个，前提是要符合条件，即interval[choice][1] <= interval[i][0]
dp数组含义：dp[i] 表示从开头到以 i 结尾的子序列的最多不重叠区间有多少个

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        intervals.sort(key = lambda x: x[0])
        n = len(intervals)
        dp = [1] * n
        for i in range(n):
            for j in reversed(range(i)): # i-1, i-1,...,0
                if intervals[j][1] <= intervals[i][0]:
                    dp[i] = max(dp[i], dp[j] + 1)
        return n - dp[n-1]

注意到方法一本质上是一个「最长上升子序列」问题，因此我们可以将时间复杂度优化至 O(n \log n)O(nlogn)，具体可以参考「300. 最长递增子序列的官方题解」。

方法二
贪心算法
子问题就是在由 intervals[i:] 这个子序列中, 找到结束时间最小的。
通过对结束时间从小到大排序，
对于每个子问题，第一个符合要求（intervals[i][0] >= right）的interval就是最优解
不用比较，不用选择，第一个就是，这就是贪心，每次找一个最值就好

class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        intervals.sort(key = lambda x: x[1])
        n = len(intervals)
        right = intervals[0][1]
        res = 1
        for i in range(1, n):
            if intervals[i][0] >= right:
                right = intervals[i][1]
                res += 1
        return n-res

下面这个解释很详细cite
在这里插入图片描述

452.用最少数量的箭引爆气球（中等）

和上一道题相同的解法，不过对非重叠区间的定义由区别，这道题因为箭射到气球边也可以射爆，那么相邻的气球算作重叠区间。所以在判断的时候是points[i][0] > right

class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        points.sort(key = lambda x: x[1])
        res = 1
        right = points[0][1]
        for i in range(1, len(points)):
            if points[i][0] > right:
                res += 1
                right = points[i][1]
        return res

2. 扫描线技巧：安排会议室

253.会议室 II（中等）

先说下题目，给你输入若干形如 [begin, end] 的区间，代表若干会议的开始时间和结束时间，请你计算至少需要申请多少间会议室。比如给你输入 meetings = [[0,30],[5,10],[15,20]]，算法应该返回 2，因为后两个会议和第一个会议时间是冲突的，至少申请两个会议室才能让所有会议顺利进行。换句话说，如果把每个会议的起始时间看做一个线段区间，那么题目就是让你求最多有几个重叠区间，仅此而已。和1094. 拼车（中等）很像，可以用差分数组做，但是这里介绍贪心算法
一图胜万言
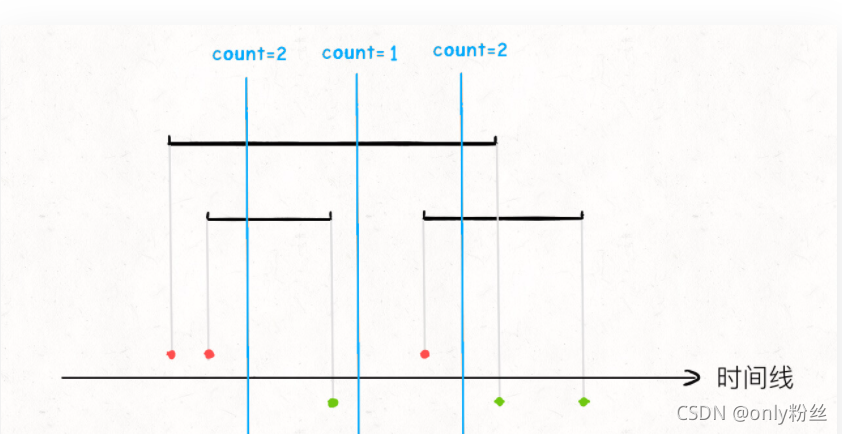
在这里插入图片描述
思路就是从左看到右，遇到红点就加一，毕竟领导要开会，会议室一定要好好布置，遇到绿色就减一，会开完了屋子跟着就不用了。和拼车一样，但是拼车还多一件事，就是可能一下来好几个乘客，所以每个红点和绿点还要跟着一个几位乘客的标签

from typing import List
def minMeetingRooms(meetings:List[List[int]])->int:
    start_list = []
    end_list = []
    for start, end in meetings:
        start_list.append(start)
        end_list.append(end)
    start_list.sort()
    end_list.sort()
    maxCount, count,i,j = 0,0,0,0
    while i < len(meetings) and j < len(meetings):
        if start_list[i] < end_list[j]:
            i += 1
            count += 1
        else:
            j += 1
            count -= 1
        maxCount = max(maxCount, count)
    return maxCount
        
meetings = [[0,30],[5,10],[15,20]]
minMeetingRooms(meetings)
# 2

3.剪视频剪出一个贪心算法

1024.视频拼接（中等）

在这里插入图片描述
方法一：
动态规划，
状态：进行到的时间
dp[i] 表示到第 i 时间时，需要最少区间数量
选择：下一个选择哪个符合条件的区间

class Solution:
    def videoStitching(self, clips: List[List[int]], time: int) -> int:
        dp = [float(inf)] * (time + 1)
        dp[0] = 0
        for i in range(1, time + 1):
            for a, b in clips:
                if a < i <= b:
                    dp[i] = min(dp[a] + 1, dp[i])
        return dp[time] if dp[time] != float(inf) else -1

方法二：
maxn = [0] * time 记录了每个时间作为起点，最远终点的位置
pre 是上一个被使用的子区间的结束位置，每次我们越过一个被使用的子区间，就说明我们要启用一个新子区间，这个新子区间的结束位置即为当前的 last。也就是说，每次我们遇到 i==pre，则说明我们用完了一个被使用的子区间。这种情况下我们让答案加 1，并更新 pre 即可。

class Solution:
    def videoStitching(self, clips: List[List[int]], time: int) -> int:
        maxn = [0] * time
        last = ret = pre = 0
        for a, b in clips:
            if a < time:
                maxn[a] = max(maxn[a], b)
        
        for i in range(time):
            last = max(last, maxn[i])
            if i == last:
                return -1
            if i == pre:
                ret += 1
                pre = last
        
        return ret

方法三
首先按起点升序排列，起点相同的按终点降序
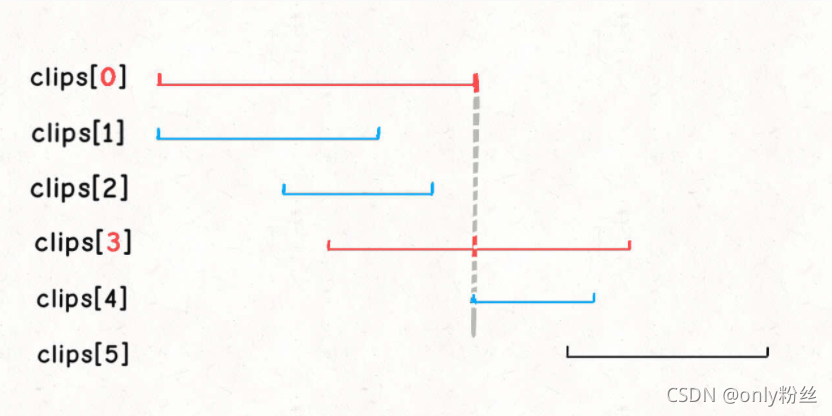
在这里插入图片描述
贪心策略就是每次选择都选择符合条件情况下（start<= right）右边界最大的当右边界大于等于T的时候就完成了剪辑

class Solution:
    def videoStitching(self, clips: List[List[int]], time: int) -> int:
        clips.sort(key = lambda x: (x[0], -x[1]))
        if clips[0][0] != 0:
            return -1
        right = clips[0][1]
        ans = 1
        i = 1
        while i < len(clips) and right < time:
            nextright = right
            # 当没有任何起点小于当前终点时，中间有空挡，无法完成
            if clips[i][0] > right:
                return -1
            # 对所有起点小于当前终点的区间， 选一个最大的终点nextright
            while i < len(clips) and clips[i][0] <= right:
                nextright = max(nextright, clips[i][1])
                i += 1
                
            right = nextright
            ans += 1
        return ans if right >= time else -1

4. 如何运用贪心思想玩跳跃游戏

55.跳跃游戏（中等）

在这里插入图片描述每一步都计算一下从当前位置最远能够跳到哪里，然后和一个全局最优的最远位置 farthest 做对比，通过每一步的最优解，更新全局最优解，这就是贪心。

class Solution:
    def canJump(self, nums: List[int]) -> bool:
        farthest = 0
        for i in range(len(nums)):
            if i > farthest:
                return False
            farthest = max(farthest, nums[i] + i)
        return True

45.跳跃游戏 II（中等）

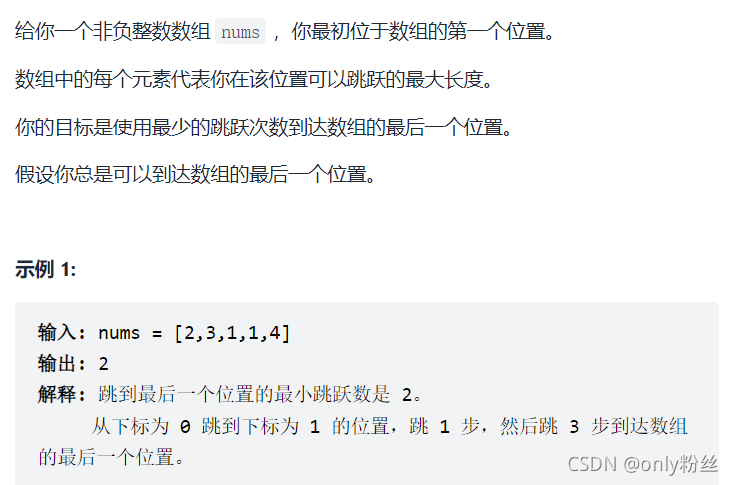
在这里插入图片描述
farthest[i] 定义是以 i 或小于 i 的位置为起点最远能到多远

class Solution:
    def jump(self, nums: List[int]) -> int:
        farthest = [0] * len(nums)
        farthest[0] = nums[0]
        for i in range(1, len(nums)):
            farthest[i] = max(farthest[i-1], i + nums[i])
        res,end = 0,0
        while end < len(nums)-1:
            end = farthest[end]
            res += 1
        return res

5. 当老司机学会了贪心算法

134.加油站（中等）

在这里插入图片描述

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        gas_left = [g - c for g,c in zip(gas, cost)]
        if sum(gas_left) < 0:
            return -1
        # 加和大于等于0 时一定存在一个解？？？
        gas_left = 2 * gas_left
        #[-2, -2, -2, 3, 3]  + [-2, -2, -2, 3, 3]
        #找最大连续子数组 的开头就是起点
        #反证法，如果不是起点，一定有一段前缀和为负数，那么这一段一定不在最大连续子数组里
        curSum = 0
        maxSum = 0
        start, end = 0, 0
        subStart = 0
        subEnd = 0
        for i in range(len(gas_left)):
            curSum += gas_left[i]
            if curSum >= 0:
                subEnd += 1
            if curSum < 0:
                subStart = i+1
                subEnd = i+1
                curSum = 0
            if curSum > maxSum:
                maxSum = curSum
                start = subStart
                end = subEnd
        return start

网上有更好的贪心算法
原理是当到 i 时如果油量小于0，那么对于从起始点到 i 中的所有的，就算tank 不为0，到 i 点的时候都小于0，那么当他们作为起始点tank 是0 的时候，到 i 点一定tank 小于0，所以起始点一定大于 i，即设定新的起始点为 i + 1并初始化tank = 0

class Solution:
    def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
        if sum(gas) -sum(cost) < 0:
            return -1
        tank = 0
        start = 0
        for i in range(len(gas)):
            tank += gas[i] - cost[i] 
            if tank < 0:
                tank = 0
                start = i + 1
        return start