动态规划----算法导论中的理解与leetcode实践

前言

动态规划（dynamic programming）：考虑“当前问题”的每种“切割”下，分化为与当前问题形式相同的子问题，这些子问题的最优解通常已在“前面”的步骤中求得并记录与备忘录（memo）中，然后在“当前问题”下，比较每种“切割”的“子最优解”，选取“最优切割方案”及对应的“子最优解”记录于备忘录中，以供后续问题作参考。
注：
（1）原问题的代价为：子问题的最优解的代价再加上这次切割的选择的直接代价；
（2）具体实施通过状态转移方程及备忘录实现
核心内容：

• 递归+记忆化→递推
• 状态的定义：opt[n]
• 状态转移方程：opt[n]=best_of(opt[n-1],opt[n-2],…)
• 最优子结构

DP与回溯算法和贪心算法的区别：

• 回溯（递归）：会带有重复计算
• 贪心：局部（当前）最优
• DP：记录局部最优子结构/多种记录值

动态规划求解的最优化问题所要具备的两个要素：
（1）最优子结构（optimal substructure）：可利用子问题的最优解进而获得整个问题的最优解；
（2）子问题重叠：子问题所在的“空间”一般很小，用来接原问题的递归算法可反复的解同样子问题

DP问题的分类：可根据备忘录的大小和每个表项所依赖的其他表项的数量对DP算法进行分类，如果一个DP算法的表格的大小为O(n^t)，每个表项依赖其他O(n^e)个表项，则称这是一个tD/tE的DP算法。
如下面的钢条切割为1D/1D，矩阵链乘法为2D/1D,最长公共子序列为2D/0D。最长回文子串为2D/0D

最优化问题的DP求解

（1）钢条切割问题（1D/1D问题）
Serling公司购买长钢条，将其切割为短钢条出售。切割工序本身没有成本支出。公司管理层希望知道最佳的切割方案。假定我们知道Serling公司出售一段长为i英寸的钢条的价格为pi(i=1,2,…，单位为美元)。钢条的长度均为整英寸。下图给出了一个价格表的样例。

问题描述：给定一段长度为n英寸的钢条和一个价格表pi(i=1,2,…n)，求切割钢条方案，使得销售收益rn最大。注意，如果长度为n英寸的钢条的价格pn足够大，最优解可能就是完全不需要切割。

问题分析：长度为n英寸的钢条共有2n-1种不同的切割方案（暴力算法），因为在距离钢条左端i(i=1,2,…n)英寸处，总是可以选择切割或不切割。
如果一个最优解将钢条切割为k段（1≤k≤n），则有
最优切割方案：

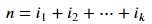
该方案下的最佳收益：

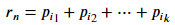
其中i为每段钢条的长度，p为对应的收益

朴素递归求解方法：将钢条从左边切割下长度为i的一段，只对右边剩下的长度为n-i的一段继续进行分析（子问题），对左边的一段则不再考虑切割：

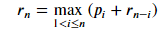
朴素递归算法之所以效率很低，是因为它反复求解相同的子问题。因此，动态规划方法仔细安排求解顺序，对每个子问题只求解一次，并将结果保存下来。如果随后再次需要此子问题的解，只需查找保存的结果，而不必重新计算。因此，动态规划方法是付出额外的内存空间来节省计算空间。

我们下面用**自底向上法（bottom-up）**方法进行求解，这种方法一般需要恰当定义子问题“规模”的概念，使得任何子问题的求解都只依赖于“更小的”子问题的求解。因此，我们可以将子问题按照规模顺序，由小至大顺序进行求解。当求解某个子问题时，它所依赖的那些更小的子问题都已求解完毕，结果已经保存。每个子问题只需求解一次，当我们求解它时，它的所有前提子问题都已求解完成。

bottom-up-cut-rod(p, n)
1    let r[0…n] be a new array
2    r[0] = 0
3    for j=1 to n
4        q = -∞
5        for i=1 to j
6            q = max(q, p[i] + r[j-i])
7        r[j] = q
8    return r[n]

注释：
1.数组r用于保存子问题（最佳收益）的解
2.长度为0的钢条没有收益
3.每种长度的钢条
4.初始化该总长度下的最优收益
5.切割位置从长度为1开始遍历，直至整根
6.求得子问题最优解
8.返回最优解（收益）

重构解（解本身，切割方案）
我们可以使用一个一维数组来存储最佳收入，另一个一维数组来存储当前长度下切割的最佳划分处

extended-bottom-up-cut-rod(p, n)
1    let r[0…n] and s[0…n] be new arrays
2    r[0] = 0
3    for j=1 to n
4        q = -∞
5        for i=1 to j
6            if q < p[i]+r[j-i]
7                q = p[i]+r[j-i]
8                s[j] = i
9        r[j] = q
10    return r and s 

注释：
6.当第一段长度为i，剩下长度为j-i，其最大收益已知为r[j-i]
7.q < p[i]+r[j-i]情况下更新q
8.记录每个总长度j下，每一段长度为i时的最优解
10.返回每种钢条总长度n下，最优收益r和第一段分割s

print-cut-rob-solution(p, n)
1    (r, s) = extended-bottom-up-cut-rod(p, n)
2    while n>0
3        print s[n]
4        n = n-s[n]

（2）矩阵链乘积（2D/1D问题）
以两个矩阵相乘为例，A1A2，A1和A2为两个矩阵，假设A1的行列数是pq，A2的行列数是qr。注意这里由于是A1乘以A2，所以A1的列数要等于A2的行数，否则无法做矩阵乘法，满足上述条件的矩阵，我们称之为“相容”的。那么对于A1A2而言，我们需要分别执行pr次对应A1的行元素乘以A2的列元素，根据线性代数知识，不难得出我们一共需要执行pq*r次乘法
问题描述：对于两个矩阵相乘，一旦矩阵的大小确定下来了，那么所需执行的乘法次数就确定下来了。那么对于两个以上的矩阵呢？是不是也是这样呢。实际上，对于多个矩阵相乘，乘法执行的次数与“划分”有关。
问题分析：我们也可以将矩阵链看成一根要分割的“钢管”，但这里记录的两个数组需要是二维的，与上面的问题不一样的是，该矩阵链“钢管”的每一段不同“质”，所以我们需要记录的不仅是从哪里“断开”，还需要记录"每一段"到哪里截止。
思路：设m[i,j]表示从i到j的矩阵链的最小计算代价，s[i,j]=k表示在i和j中间的矩阵k后面加一个括号，则m的递推方法是：

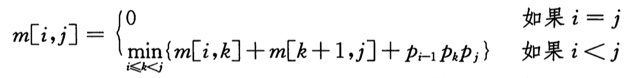
第一项是前半部分，第二项是后半部分，第三项是前后两部分组合的计算代价。最终m[1,n]就是最小代价。由于是ijk三重遍历，所以复杂度是O(n3)；所以m[i,j]的值给出了子问题最优解的代价，s[i,j]保存了矩阵链i到j最优括号化的分割点位置k。
自底向上：

MAXTRIX_CHAIN_ORDER(p)     # 输入矩阵大小的序列<p0,p1,p2,...pn>
1  n = length[p]-1;
2  let m[1,...,n,1...n] and s[1,...,n,1...n] be new tables
3  for i=1 to n
4      do m[i][i] = 0;
5  for l = 2 to n  //t is the chain length
6      do for i=1 to n-l+1
7             j=i+l-1;
8             m[i][j] = MAXLIMIT;
9             for k=i to j-1
10                  q = m[i][k] + m[k+1][i] + qi-1qkqj;
11                  if q < m[i][j]
12                         m[i][j] = q;
13                         s[i][j] = k;
14 	return m and s;

注释：
1.总长度为n的矩阵链
2.初始化最优解表格m，重构解表格s
3.对所有的i计算m[i,i]=0
5.列举每种长度l的矩阵链，对所有的i，计算m[i,i+l]的最小计算代价
6.列举每个初始点i
7.由i，l即可确定终点j
8.初始化当前问题最优计算代价
9.列举划分点
10.由序列p以及最优解的memo m得到候选解q
11.计算m[i,j]时依赖于已经计算出的表项m[i,k]和m[k,j]
12.满足条件下更新m[i,j]，s[i,j]

(3)最长公共子序列（2D/0D问题）
一个数列S，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则 S 称为已知序列的最长公共子序列（Longest Common Sequence）。
例如：输入两个字符串BDCABA和 ABCBDAB，字符串 BCBA和BDAB 都是是它们的最长公共子序列，则输出它们的长度4，并打印任意一个子序列. （Note: 不要求连续）
问题分析：
DP方法：
设序列 X=<x1, x2, …, xm> 和 Y=<y1, y2, …, yn> 的一个最长公共子序列 Z=<z1, z2, …, zk>，则：
（1）若 xm = yn，则 zk = xm = yn ，且 Zk-1 是 Xm-1 和 Yn-1 的最长公共子序列；
（2）若 xm ≠ yn， 要么Z是 Xm-1 和 Y 的最长公共子序列，要么 Z 是X和 Yn-1 的最长公共子序列：
2.1)若 xm ≠ yn 且 zk≠xm ，则 Z是 Xm-1 和 Y 的最长公共子序列；
2.2)若 xm ≠ yn 且 zk ≠yn ，则 Z 是X和 Yn-1 的最长公共子序列
综合一下：就是求二者的大者

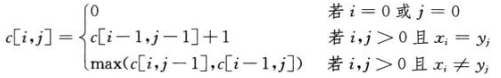
LCS-LENGTH(X, Y):
m = X.length
n = Y.length
let b[1...m, 1...n] and c[0...m, 0...n] be new table

for i = 1 to m
    c[i, 0] = 0
for j = 1 to n
    c[0, j] = 0

for i = 1 to m                           # 列举X的各种长度
    for j = 1 to n                       # 列举Y的各种长度
    
        if x[i] == y[j]                  # 情况（1）
           c[i,j] = c[i-1, j-1]+1
           b[i,j] = 'diag'

        elseif c[i-1, j] >= c[i, j-1]    # 情况2.1)
            c[i,j] = c[i-1, j]
            b[i,j] = 'up'

        else                             # 情况2.2)
            c[i,j] = c[i, j-1]
            b[i,j] = 'left'

return c and b                           # 返回最优解c和重构解b

leetcode实战

5.Longest Palindromic Substring（最长回文子串）
问题描述：
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:
Input: “babad”
Output: “bab”
Note: “aba” is also a valid answer.

Example 2:
Input: “cbbd”
Output: “bb”
即给定一个字符串S，找出其中的最长回文子串，并返回该子串。

动态规划解法思路：在暴力搜索法的基础上，加入“备忘录”以达到减少重复计算的目的（如判断“ababa”为回文，当已知“bab”为回文时，仅需知道最左字符和最右相同即可）
定义目标字符串的第i个字符到第j个字符是否为回文为p(i,j)（状态的定义），有：

那么状态转移方程为：

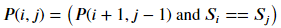
基本情况为：

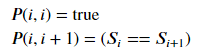
class Solution():
    def longestPalindrome(self, s):
        if not s:
            return ""
        lens=len(s)
        if lens<2:
            return s
        maxlen=0                               # 初始化 最长回文长度
        start=0                                # 初始化 回文起始位置
        dp=[[0]*lens for row in range(lens) ]  # dp数组 维护字串状态

        #step 1  初始化dp数组,完成长度小于3的子串状态判断
        
        for i in range(lens):          # i 为字符索引
            dp[i][i]=1
            if i<lens-1 and s[i]==s[i+1]:
                print (i,":",s[i]," ",i+1,':' ,s[i+1] )
                dp[i][i+1]=1
                start=i                               
                maxlen=2                           

        #step 2  i为子串长度，j为子串起始地址，r为子串结束地址
        #        逐步得到长度为i的子串状态，利用状态转移方程完成这一判断
        
        for i in range(3,lens+1):                # 遍历子串长度为3以上的子串 
            for j in range(0,lens-i+1):          # 子串起始索引
                r=j+i-1                          # 根据长度i得到终止索引
                if dp[j+1][r-1] and s[j]==s[r]:  # 状态转移方程
                    dp[j][r]=1
                    maxlen=i                     # 更新回文长度
                    start=j

        #step 3 根据第二步得到的最长子串长度和起始位置，得到最终结果
        if maxlen>=2:
            return s[start:start+maxlen]
        return s[0]

120.Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle

[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

Note:

Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
问题描述：将一个二维数组排列成金字塔的形状，找到一条从塔顶到塔底的路径，使路径上的所有点的和最小，从上一层到下一层只能挑相邻的两个点中的一个。
问题分析：把triangle二维数组转化，每一行的数列都左对齐，使其上一行到下一行就两个选择，横坐标不变或加一

class Solution(object):
    def minimumTotal(self, triangle):
        n = len(triangle)

        dp = triangle[-1] # 创建与金字塔底层同样长度的dp数组，记录状态，初始化为底层元素
                          # dp[i]表示从底层到这一层的第i个元素所有路径中最小的和

        for i in range(n-2,-1,-1):  # 从倒数第二行开始
            for j in range(i+1):    # 每行的每个元素计算最优值
                # 递推关系：
                # 下一行与它相邻的两个节点中比较小的再加上它自己的值
                # 从倒数第二层开始网上，变化数字，dp[-1]一开始就用不到了
                dp[j] = min( dp[j], dp[j+1] ) + triangle[i][j]
        return dp[0]