本文详细介绍了多元微分的基本概念，包括n维空间、二元函数、偏导数及其计算，以及方向导数、梯度和Hessian矩阵。此外，还探讨了函数的极值与最值，包括无条件极值和条件极值（拉格朗日乘子法），并讨论了基于梯度的优化方法，如梯度下降法和牛顿迭代法。这些理论在机器学习和最优化问题中有着广泛应用。
文章目录
多元微分求偏导
多元函数相关概念
n维空间
设 n n n为取定的一个正整数，我们用 R n R^n Rn表示 n n n元有序实数组 ( x 1 , x 2 , . . . , x n ) (x_1,x_2,...,x_n) (x1,x2,...,xn)的全体所构成的集合，即
KaTeX parse error: Expected 'EOF', got '}' at position 88: …, i = 1,2,...,n}̲
R n R^n Rn中的元素 ( x 1 , x 2 , . . . , x n ) (x_1,x_2,...,x_n) (x1,x2,...,xn)有时也用单个字母 x x x来表示，即 x = ( x 1 , x 2 , . . . , x n ) x = (x_1,x_2,...,x_n) x=(x1,x2,...,xn).当所有的 x i ( i = 1 , 2 , . . . , n ) x_i(i = 1,2,...,n) xi(i=1,2,...,n)都为零时，称这样的元素为 R n R^n Rn中的零元，记为0或O。在解析几何中，通过直角坐标系， R 2 R^2 R2（或 R 3 R^3 R3）中的元素分别与平面（或空间）中的点或向量建立一一对应的关系。
为了在集合 R n R^n Rn中的元素之间建立联系，在 R n R^n Rn中定义线性运算如下：
x + y = ( x 1 + y 1 , x 2 + y 2 , . . . , x n + y n ) λ x = ( λ x 1 , λ x 2 , . . . , λ x n ) x + y = (x_1 + y_1 , x_2 + y_2, ... , x_n + y_n) \\ \lambda x = (\lambda x_1, \lambda x_2, ..., \lambda x_n) x+y=(x1+y1,x2+y2,...,xn+yn)λx=(λx1,λx2,...,λxn)
这样定义了线性运算的集合 R n R^n Rn称为 n n n维空间。
此外， R n R^n Rn中点 x x x和点 y y y之间的距离，记作 ρ = ( x , y ) \rho = (x, y) ρ=(x,y)，规定
ρ = ( x , y ) = ( x 1 + y 1 ) 2 + ( x 2 + y 2 ) 2 + . . . + ( x n + y n ) 2 \rho = (x, y) = \sqrt{
{(x_1 + y_1)}^2 + {(x_2 + y_2)}^2 + ... + {(x_n + y_n)}^2} ρ=(x,y)=(x1+y1)2+(x2+y2)2+...+(xn+yn)2
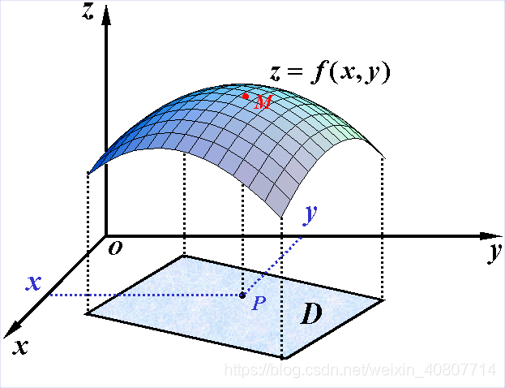
二元函数
设 D D D是 R 2 R^2 R2的一个非空子集，称映射 f : D − > R f:D->R f:D−>R为定义在 D D D上的二元函数，通常记为
z = f ( x , y ) , ( x , y ) ∈ D z = f(x, y) , (x,y) \in D z=f(x,y),(x,y)∈D
或
z = f ( P ) , P ∈ D z = f(P) , P \in D z=f(P),P∈D
求偏导数
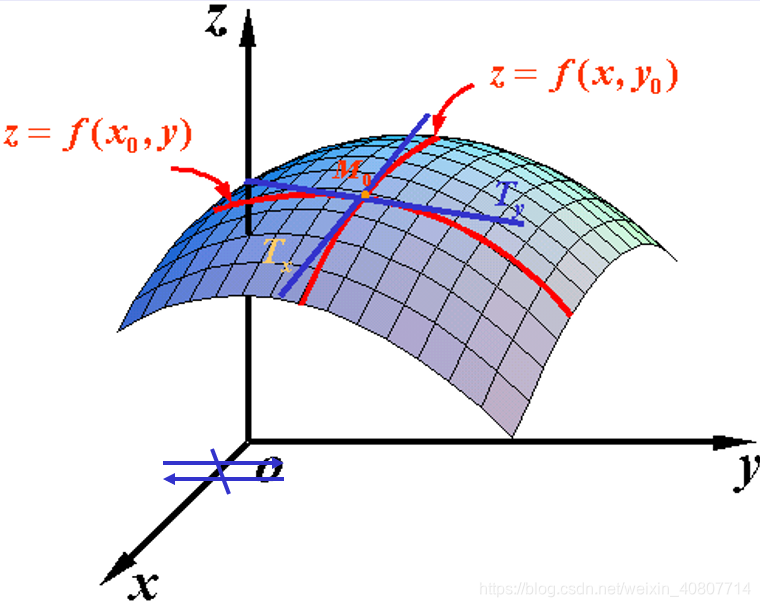
个人理解：为什么要求偏导，而不是像在一元函数中那样求导数？在一元函数中，我们仅需要求解 f ( x ) f(x) f(x)对 x x x的导数即可获得函数的性态，因为此时 f ( x ) f(x) f(x)只与 x x x对应。而在多元函数（这里以二元函数为例）中， f ( x , y ) f(x,y) f(x,y)与 x x x和 y y y对应。观察下图，我们发现，此时， M 0 M_0 M0点的方向不再固定，为了能够更好地描述函数性态，我们主要对 x x x和 y y y两个方向进行求导，也就是 f ( x , y ) f(x,y) f(x,y)分别对 x x x和 y y y求偏导数，类似于做降维处理（一元函数求导），简化了计算。当然，从数学角度讲，可能延伸到求二元极限（导数的定义）、求全微分等内容，这里不作展开。
偏导数定义如下图：
举例：求 z = x 2 + 3 x y + y 2 z = x^2 + 3xy + y^2 z=x2+3xy+y2在点 ( 1 , 2 ) (1,2) (1,2)处的偏导数。
把 y y y看做常数，得
∂ z ∂ x = 2 x + 3 y \frac{\partial z}{\partial x} = 2x + 3y ∂x∂z=2x+3y
把 x x x看做常数，得
∂ z ∂ y = 3 x + 2 y \frac{\partial z}{\partial y} = 3x + 2y ∂y∂z=3x+2y
将 ( 1 , 2 ) (1,2) (1,2)带入上面结果即可求解。
方向导数求梯度
在上一小节中，提到了多元函数求偏导时的方向问题。这里就引出了方向导数，那么方向导数可以理解为在函数定义域内的某一点，对该点的某一方向求得的导数。结合一元导数的意义（变化率），可以进一步理解为一个函数沿指定方向的变化率。
以下图为例，可以把它看作“山”的模型，而山的表面可以通过一个函数来表达。此时，我们在山上的某一点想要下山。在下山的过程中，我们总是有很多的方向（方向导数）可以选择，有的方向可以引导我们更快地下山，有的方向甚至可以引导我们上山，那么沿着哪个方向才是最快的下山路径？这就引出了梯度这一概念。
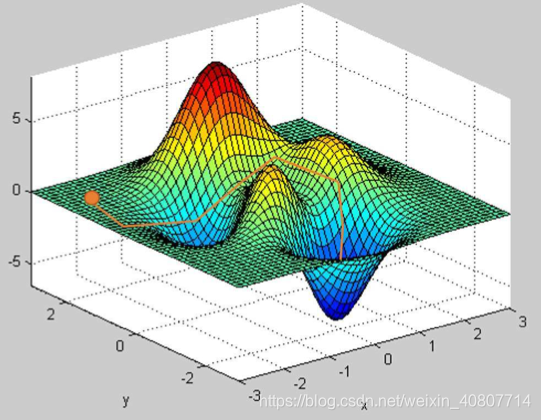
通过上面的例子，易知梯度是有方向的，它是一个向量，这与方向导数有本质的区别（方向导数本质上是数值，可以直观理解为“下山”例子中的“下山速度”）。
梯度表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（该梯度的方向）变化最快，变化率最大（该梯度的模）。
定义：设二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在平面区域 D D D上具有一阶连续偏导数，则对于每一个点 P ( x , y ) P(x,y) P(x,y)都可定义出一个向量 { ∂ f ∂ x , ∂ f ∂ y } = f x ( x , y ) i + f y ( x , y ) j \{\frac{\partial f}{\partial x} , \frac{\partial f}{\partial y}\} = f_{x}(x,y)\boldsymbol{i} + f_{y}(x,y)\boldsymbol{j} {
∂x∂f,∂y∂f}=fx(x,y)i+fy(x,y)j，该函数就称为函数 z = f ( x , y ) z=f(x,y) z=f(x,y)在点 P ( x , y ) P(x,y) P(x,y)的梯度，记为 g r a d f ( x , y ) \boldsymbol{grad} {\,} f(x,y) gradf(x,y)或 ∇ f ( x , y ) \nabla {\,} f(x,y) ∇f(x,y)。
其中， ∇ \nabla ∇称为（二维的）向量微分算子或Nabla算子。
举例：计算 f ( x , y ) = x 2 + y 2 f(x,y) = x^2 + y^2 f(x,y)=x2+y2的梯度向量。
一阶偏导求Jacobian矩阵
假设𝐹:ℝ𝑛→ℝ𝑚是一个从 n n n维欧氏空间映射到 m m m维欧氏空间的函数。该函数由 m m m个实函数组成: y 1 ( x 1 , . . . , x n ) , . . . , y m ( x 1 , . . . , x n ) y_1(x_1, ... , x_n) , ... , y_m(x_1, ... , x_n) y1(x1,...,xn),...,ym(x1,...,xn)。这些函数的偏导数（如果存在）可以组成一个 m m m行 n n n列的矩阵，这个矩阵就是所谓的Jacobian（雅可比）矩阵：
[ ∂ y 1 ∂ x 1 ⋯ ∂ y 1 ∂ x n ⋮ ⋱ ⋮ ∂ y m ∂ x 1 ⋯ ∂ y m ∂ x n ] \left[ \begin{matrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{matrix} \right] ⎣⎢⎡∂x1
最低0.47元/天 解锁文章
扫一扫
887
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
