视频背景建模主要使用到:
高斯混合模型(Mixture Of Gauss,MOG)
基于混合高斯模型去除背景法
高斯模型去除背景法也是背景去除的一种常用的方法,经常会用到视频图像侦测中。这种方法对于动态的视频图像特征侦测比较适合,因为模型中是前景和背景分离开来的。分离前景和背景的基准是判断像素点变化率,会把变化慢的学习为背景,变化快的视为前景。
一、理论
混合高斯背景建模是基于像素样本统计信息的背景表示方法,利用像素在较长时间内大量样本值的概率密度等统计信息(如模式数量、每个模式的均值和标准差)表示背景,然后使用统计差分(如3σ原则)进行目标像素判断,可以对复杂动态背景进行建模,计算量较大。
在混合高斯背景模型中,认为像素之间的颜色信息互不相关,对各像素点的处理都是相互独立的。对于视频图像中的每一个像素点,其值在序列图像中的变化可看作是不断产生像素值的随机过程,即用高斯分布来描述每个像素点的颜色呈现规律【单模态(单峰),多模态(多峰)】。
对于多峰高斯分布模型,图像的每一个像素点按不同权值的多个高斯分布的叠加来建模,每种高斯分布对应一个可能产生像素点所呈现颜色的状态,各个高斯分布的权值和分布参数随时间更新。当处理彩色图像时,假定图像像素点R、G、B三色通道相互独立并具有相同的方差。对于随机变量X的观测数据集{x1,x2,…,xN},xt=(rt,gt,bt)为t时刻像素的样本,则单个采样点xt其服从的混合高斯分布概率密度函数:
其中k为分布模式总数,η(xt,μi,t, τi,t)为t时刻第i个高斯分布,μi,t为其均值,τi,t为其协方差矩阵,δi,t为方差,I为三维单位矩阵,ωi,t为t时刻第i个高斯分布的权重。
详细算法流程:


createBackgroundSubtractorMOG2(int history=500, double varThreshold=16,bool detectShadows=true);- 1
K最近邻(k-NearestNeighbor,kNN)
 用了之后,发现我用的都是KNN,所以查阅了一下相关文献,才对KNN理解正确了,真是丢人了。
用了之后,发现我用的都是KNN,所以查阅了一下相关文献,才对KNN理解正确了,真是丢人了。
左图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:如果一个样本在特征空间中的k个最相 似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决 策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方 法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
 用了之后,发现我用的都是1NN,所以查阅了一下相关文献,才对KNN理解正确了,真是丢人了。
用了之后,发现我用的都是1NN,所以查阅了一下相关文献,才对KNN理解正确了,真是丢人了。
左图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:如果一个样本在特征空间中的k个最相 似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决 策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方 法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
kNN算法本身简单有效,它是一种lazy-learning算法,分类器不需要使用训练集进行训练,训练时间复杂度为0。kNN分类的计算复杂度和训练集中的文档数目成正比,也就是说,如果训练集中文档总数为n,那么kNN的分类时间复杂度为O(n)。
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成正比。
该算法在分类时有个主要的不足是,当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的 K个邻居中大容量类的样本占多数。因此可以采用权值的方法(和该样本距离小的邻居权值大)来改进。该方法的另一个不足之处是计算量较大,因为对每一个待分 类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。目前常用的解决方法是事先对已知样本点进行剪辑,事先去除对分类作用不大的样本。该 算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
createBackgroundSubtractorKNN(int history=500, double dist2Threshold=400.0, bool detectShadows=true);- 1
history:history的长度。
varThreshold:像素和模型之间马氏距离的平方的阈值。
detectShadows:默认为true,检测阴影并标记它们(影子会被标记为灰色)。 会降低了部分速度。
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main(int argc, char**) {
VideoCapture capture(0);//调用摄像头
//capture.open("F:/video_003.avi");
if (!capture.isOpened()) {
printf("could not find the video file...\n");
return -1;
}
// create windows
Mat frame;
Mat bsmaskMOG2, bsmaskKNN;
namedWindow("input video", CV_WINDOW_AUTOSIZE);
namedWindow("MOG2", CV_WINDOW_AUTOSIZE);
namedWindow("KNN Model", CV_WINDOW_AUTOSIZE);
//形态学开操作
Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3), Point(-1, -1));
// intialization BS
//高斯混合模型背景建模
Ptr<BackgroundSubtractor> pMOG2 = createBackgroundSubtractorMOG2();
//KNN-K个最近邻
Ptr<BackgroundSubtractor> pKNN = createBackgroundSubtractorKNN();
while (capture.read(frame)) {
imshow("input video", frame);
// MOG BS
pMOG2->apply(frame, bsmaskMOG2);//
//形态学开操作去噪点
//对处理后的帧进行开操作,减少视频中较小的波动造成的影响
morphologyEx(bsmaskMOG2, bsmaskMOG2, MORPH_OPEN, kernel, Point(-1, -1));
imshow("MOG2", bsmaskMOG2);//高斯混合模型背景模型
// KNN BS mask
pKNN->apply(frame, bsmaskKNN);
morphologyEx(bsmaskKNN, bsmaskKNN, MORPH_OPEN, kernel, Point(-1, -1));//形态学开操作去噪点
imshow("KNN Model", bsmaskKNN);//KNN背景模型
char c = waitKey(50);
if (c == 27) {
break;
}
}
capture.release();
waitKey(0);
return 0;
} 用了之后,发现我用的都是1NN,所以查阅了一下相关文献,才对KNN理解正确了,真是丢人了。
用了之后,发现我用的都是1NN,所以查阅了一下相关文献,才对KNN理解正确了,真是丢人了。
左图中,绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:如果一个样本在特征空间中的k个最相 似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。KNN算法中,所选择的邻居都是已经正确分类的对象。该方法在定类决 策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 KNN方法虽然从原理上也依赖于极限定理,但在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方 法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
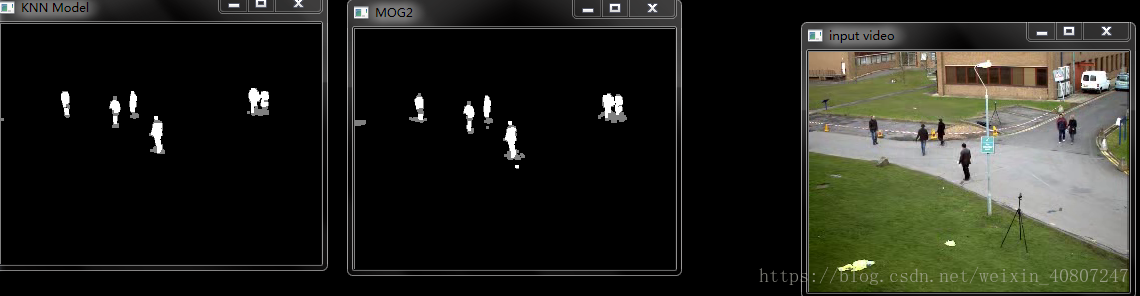








 本文介绍了视频背景建模中的两种主流方法:高斯混合模型(MOG)和K最近邻(KNN)算法。高斯混合模型能够处理复杂的动态背景,而KNN算法则适用于样本不平衡的情况。此外,还提供了这两种方法的具体实现代码。
本文介绍了视频背景建模中的两种主流方法:高斯混合模型(MOG)和K最近邻(KNN)算法。高斯混合模型能够处理复杂的动态背景,而KNN算法则适用于样本不平衡的情况。此外,还提供了这两种方法的具体实现代码。
















 576
576

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








