[STL]树

GITHUB：红黑树
《STL源码剖析》

二叉搜索树

---

二叉搜索树在平衡的情况下，可提供对数时间的元素插入和访问。

查找与插入

如果二叉查找树相对平衡，那么查找和插入的复杂度为O(logN)。

1. 查找
查找某个元素很简单，从根节点开始，根据根节点的值确定要在左子树还是右子树上搜索即可，如果到达尾端NULL节点，则表示元素不存在。
如果要在某个二叉搜索树中找到最大元素或最小元素，也是一件很简单的事情：一直往左走或者一直往右走即可。

2. 插入
插入新元素时，从根节点开始，遇到键值较大的就往左，遇到键值较小的就往右，一直到尾端，即为插入的位置。

删除

如果二叉查找树相对平衡，那么删除的复杂度为O(logN)。

假设要删除旧节点A，情况分为3种：

1. A没有子节点：直接删除即可；
2. A有一个子节点：直接将A的子节点连至A的父节点，再将A删除：
   
3. A有两个子节点：用A的右子树中的最小的节点取代A（前面说到，查找某个二叉搜索树的最小元素，只需要一直向左走到底即可）：
   

二叉搜索树的平衡

二叉搜索树在比较平衡的状态下才具有较好的性能，“平衡”的大致意义是：没有任何一个节点过深（深度过大）。不同的平衡条件，造就不同的效率表现，以及不同的实现复杂度。

平衡二叉搜索树的种类有多种：AVL-tree，RB-tree。

AVL tree

---

AVL树是一个”加上了额外平衡条件“的二叉搜索树，其平衡条件的建立是为了确保整棵树的深度为O(logN)。直观上的最佳平衡条件是每个节点的左右子树都有着相同的高度，但这样的平衡条件很难达到。AVL tree退而求其次，要求任何节点的左右子树高度相差<=1。

向AVL tree中插入节点，平衡条件可能会被破坏。假设节点X的平衡条件被破坏，则具体有以下四种情况：

1. 插入点位于X的左子节点的左子树——左左；
2. 插入点位于X的左子节点的右子树——左右；
3. 插入点位于X的右子节点的左子树——右左；
4. 插入点位于X的右子节点的右子树——右右。

情况1,4彼此对称，称为外侧插入，可以用单旋（左旋或右旋）操作进行调整；
情况2,3彼此对称，称为内侧插入，可以用双旋操作进行调整。

单旋转

下面展示插入节点11之后导致节点k2不平衡的例子（左左），在该例子中，k2的左子树深度为3，右子树的右子树深度为2。调整的方法（其实就是右旋）见下图：

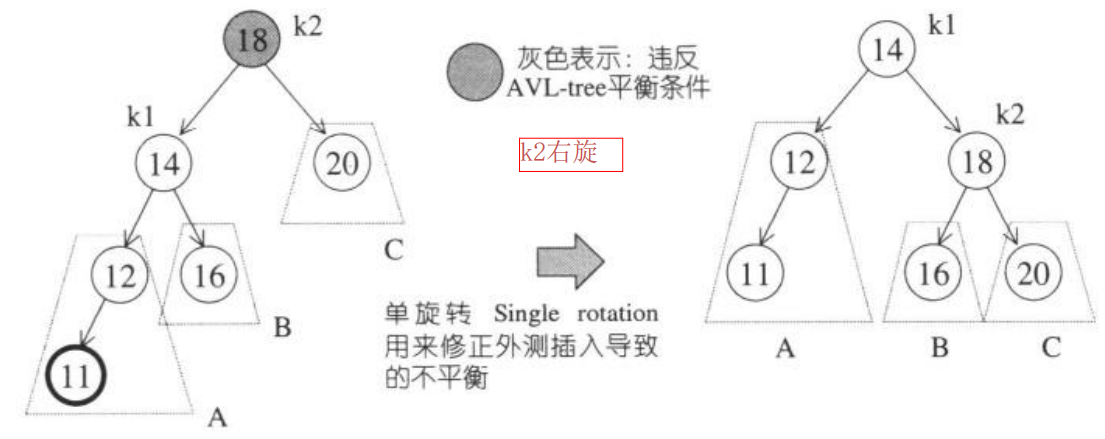
双旋转

举一个“左右”的例子：

红黑树

---

红黑树本质上就是一棵二叉搜索树，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证红黑树的查找，插入，删除时间复杂度最坏为O(log n)。

红黑树具有5个性质：

• 每个节点要么是红的，要么是黑的；
• 根节点是黑的；
• 每个叶节点（NULL节点）都是黑的；
• 如果一个节点是红色的，那么它的两个子节点都是黑的；
• 对于任一节点而言，其到叶子节点的每一条路径都包含相同数量的黑节点。

上面的5个性质使得一棵n个节点的红黑树始终保持log n 的高度，从而使得红黑树的查找，删除，插入的时间复杂度最坏为O(log n)。下面是一棵红黑树的例子：

红黑树的旋转

---

为了保证红黑树的相对平衡，经常需要进行重新着色，旋转（左旋和右旋就是前面提到的单旋）操作：

1.左旋
例如要对节点2进行左旋：

具体过程如下：

左旋完毕之后，仍然满足二叉查找树的性质。

2.右旋
与左旋差不多：

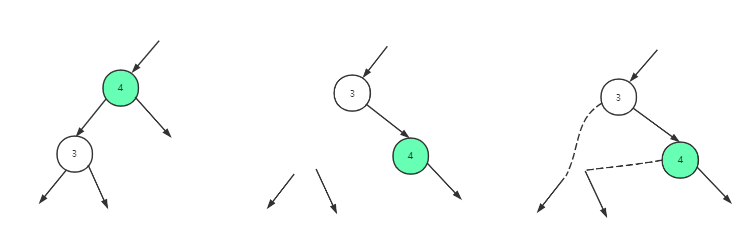
红黑树的插入

假设新节点为X，其父节点为P，祖父节点为G，伯父节点（父节点的兄弟）为S，曾祖父节点为GG。现在，根据二叉查找树的规则，新节点X必须是叶子节点。根据红黑树规则5，X必须是红色的。若P是黑色的，那么将不会违反规则。若P也是红色的，就会违反规则4。而P为红色意味着G一定是黑色的（由规则4）。于是，根据X的插入位置及外围节点（S和GG）的颜色，有以下四种考虑：

1. 状况1：S为黑且X为外侧插入。对此情况，我们先对P，G做一次单旋转，再改变P，G颜色，即可重新满足红黑树的规则4：
   
2. 状况2：S为黑且X为内侧插入。对此情况，我们需要1）先对P，X做一次单旋转；2）更改G，X的颜色；3）再对G做一次单旋转：
   
   
   

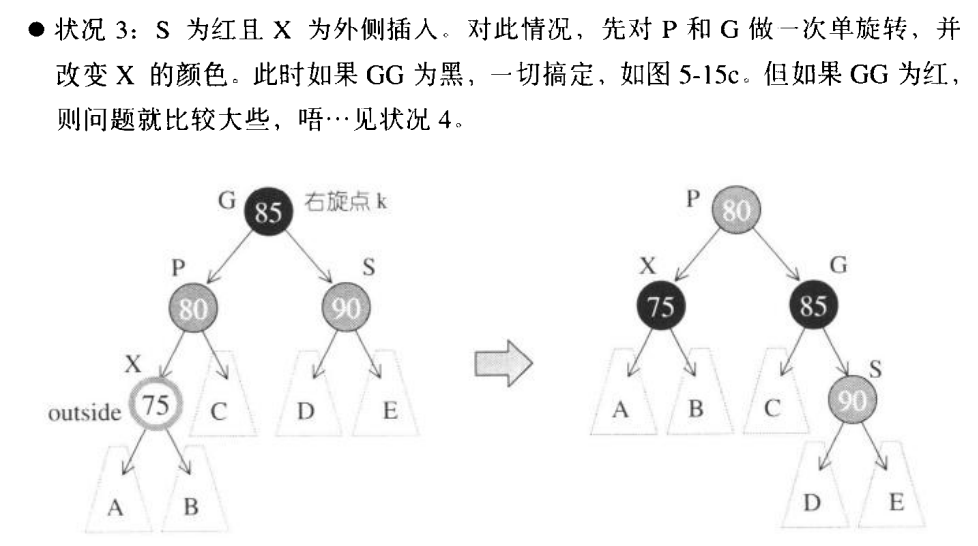
红黑树的删除

红黑树的迭代器

红黑树的实现

一棵红黑树初始化的时候只有一个header：

header结点(root的父节点)，同时也是end()节点：
parent: root
right: 最大的节点
left: 最小的节点

https://www.cnblogs.com/wangjzh/p/4049598.html

//寻找node节点的下一个节点
void increment()
{

}