浅析动态规划-leetcode最大子序和，买卖股票的最佳时间

自言自语

昨天在leetcode上遇到两个难度为简单的题，但是花了很长时间都没做出来，极度的郁闷怀疑自己的智商。看到题解后又感叹这种巧妙的办法是怎么想出来的。其实这两个问题都是用大名鼎鼎的“动态规划”破解的，要是掌握了动态规划的通式方法，其实也并不难。

动态规划

在知乎上看到一个很有意思的解释，大概是这么个意思：
请求出1+1+1+1+1+1+1+1=？数了数8个1，等于8。那么再+1等于多少呢，很快你就可以得出9。为什么这么快呢，因为后面这个问题是前面问题的答案+1。
这就是动态规划最重要的思想，有点像高中数学求数列的通式，动态规划也是要发掘出”当前阶段的状态如何通过之前计算过的阶段状态得到“。数学的角度就是，f(n) 和f(n-1) 之间的关系。
这种关系，我们称之为：状态转移方程;
而且依据问题的复杂程度，状态转移方程的维度也会增加，一般一个状态一个维度

最大子序和

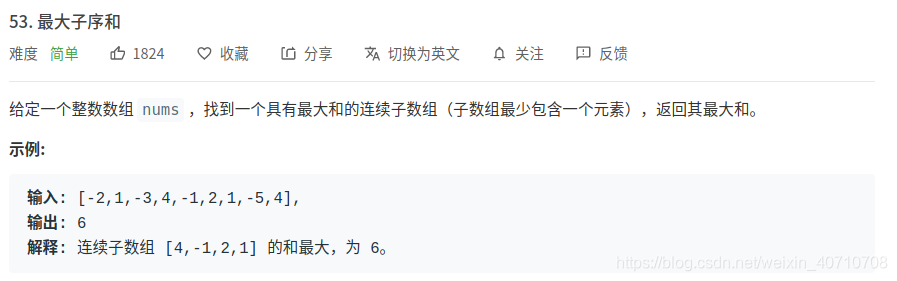找出状态转移方程：
当前位置的最大子序和，是”上一个位置的最大子序和+当前位置的大小的和，和当前位置的大小“更大的那个：
f(i) = max(f(i-1)+nums[i],nums[i])
这样得出的f(i)是经过i这个位置的最大子序和，而我们要的是全局的最大子序和，因此要挑出所有f(i)中最大的;

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int len = nums.size();
        int dp0[len];
        dp0[0]=nums[0];
        int maxx = nums[0];
        for(int i=1;i<len;i++)
        {
            dp0[i]=max(dp0[i-1]+nums[i],nums[i]);
            cout<<dp0[i];
            maxx = max(maxx,dp0[i]);     
        }
        return maxx;
        
    }
};

买卖股票的最佳时机

当前的最大收益，取决于前一天能达到的最大收益和今天的最大收益（今天的价格减去前面最小的价格）哪个更大：
f(i) = max(f(i-1),prices[i]-min)

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if(len == 0)
        return 0;
        int minx = prices[0];
        int dp[len];
        dp[0]=0;
        for(int i=1;i<len;i++)
        {
            minx = min(prices[i],minx);
            dp[i] = max(dp[i-1],prices[i]-minx);
        }
        return dp[len-1];
    }
};