采用硬限幅函数时单个神经元的分类功能

代码

import numpy as np
from matplotlib import pyplot as plt
import random
plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文标签
plt.rcParams['axes.unicode_minus'] = False

def yxf(x):
    if x >= 0:
        return 1
    else:
        return 0


def juzheng(a,b):
    sum = 0
    for i in range(len(a)):
        sum = sum + a[i]*b[i]
    return sum


w = [0.0, 0.0, 1.0]
x0_r = []
x1_r = []
label = []
for i in range(200):
    x0 = random.randint(-10, 10)
    x1 = random.randint(-10, 10)
    if 0.5*x0 + x1 - 1 < 0:
        x0_r.append(x0)
        label.append(0)
        x1_r.append(x1)
    elif 0.5*x0 + x1 - 1 > 0:
        x0_r.append(x0)
        label.append(1)
        x1_r.append(x1)
plt.figure()
xx = np.linspace(-10, 10, 100)
err = 1
k = 0
while err > 0:
    tj = []
    for i in range(len(label)):
        X1 = [x0_r[i], x1_r[i], 1]
        I1 = juzheng(X1, w)
        y = yxf(I1)
        dui = label[i] - y
        w[0] = w[0] + 0.01 * dui * X1[0]
        w[1] = w[1] + 0.01 * dui * X1[1]
        w[2] = w[2] + 0.01 * dui * X1[2]
        tj.append(abs(dui))
    plt.clf()
    plt.ylim([-15, 15])
    for j in range(len(label)):
        if label[j] == 1:
            plt.plot(x0_r[j], x1_r[j], 'g*')
        elif label[j] == 0:
            plt.plot(x0_r[j], x1_r[j], 'ks')
    # plt.plot(X1[0], X1[1], '1', markersize=10)
    if w[1] != 0:
        yy = -w[2] / w[1] - w[0] / w[1] * xx
        plt.plot(xx, yy, label='当前曲线')
        yy1 = 1 - 0.5 * xx
        plt.plot(xx, yy1, label='理想曲线')
        # plt.pause(0.001)
        plt.legend()
    k = k + 1
    err = sum(tj)
    sss = '第'+str(k)+'次迭代.jpg'
    sss1 = '有'+str(err)+'个点不满足条件'
    plt.title(sss1)
    plt.savefig(sss)
    print('第{}次迭代不满足条件的点有{}个'.format(k, err))

求解结果

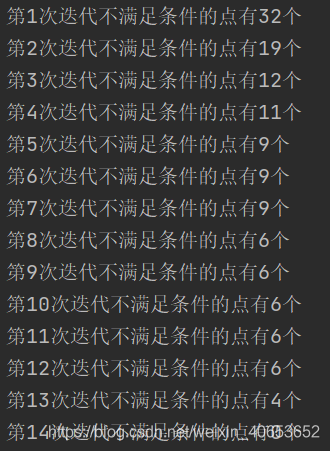
结论

对于线性可分的问题，采用硬限幅函数的学习算法是收敛的。若l(k)已经很接近最佳分界线 ，那么步幅α必须选得非常小，否则可能矫枉过正，使W(k+1)转过了头，但如果步幅选得很小，学习速度将变得很慢，为了解决这个矛盾，可以采取变步幅的方案。