KTzhu算法第一届第一期（线性拟合）

自我研究内容

1.线性拟合定义

取自百度词条：已知某函数的若干离散函数值{f1,f2,…,fn}，通过调整该函数中若干待定系数f(λ1, λ2,…,λm), 使得该函数与已知点集的差别(最小二乘意义)最小。如果待定函数是线性，就叫线性拟合或者线性回归。

2.线性拟合定义理解

根据百度知道：线性拟合和线性回归的的区别是什么？
拟合是国内的传统讲法，用一条直线代替样本点，以达到预测的作用
举例：比如拟合每天学习时间和高考成绩，可能就是线性的。
但若拟合收入高低和幸福指数，那很可能就不是了，因为不是说赚的越高越高兴，而且可能到了很高的水平，收入增加了很多，却幸福不起来，数据有可能是指数，有可能是二次函数，这些都归为非线性。

3.一类问题的基本描述

已知一系列的离散数据点（X,Y）X,求，当x=xq时，所对应的Y值Y=Yq？

X1	X2	X3	…	Xn
Y1	Y2	Y3	…	Yn

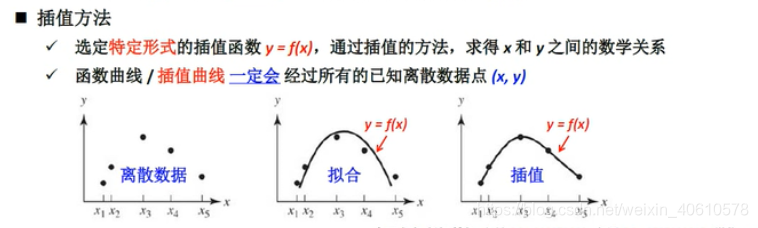
构造出一个函数y=f(x)来逼近/近似代替离散数据点（X,Y）所对应的数学关系：
数据拟合（fitting）
数据差值（interpolation）

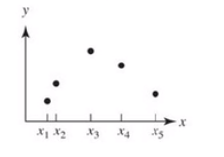
离散数据点

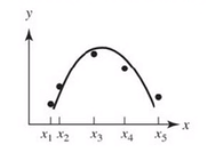
数据拟合

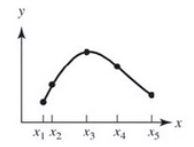
数据插值

拟合与插值的区别

来自上下求索博主教学视频

概念一：最小二乘法

百度百科定义：最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

线性最小二乘的基本公式

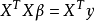
自我疑问

1. 最小二乘法的求解方式
2. 线性拟合与曲线拟合的关系

疑问解答

总结