支持向量机学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
1、线性可分支持向量机学习算法------最大间隔法(硬间隔)

函数间隔y‘的取值对上面的不等式约束没有影响,对目标函数的优化也无影响。

至于等价问题为什么要是平方乘以1/2的系数是因为要将问题转化为凸2次优化问题,便于求解。
如此,就将问题转为成了一个凸2次优化问题。

最终求解可以得到w、b,以及超平面。
在决定分离超平面时只有支持向量起作用,其他实例点并不起作用。支持向量的个数一般很少,所以支持向量机由很少的“重要”的训练样本确定。
2、学习的对偶算法
在约束优化问题中,常常利用拉格朗日对偶性将原始问题转化成对偶问题。通过解对偶问题的解得到原始问题的解。
1)首先需要搞清原始问题与对偶问题的关系:
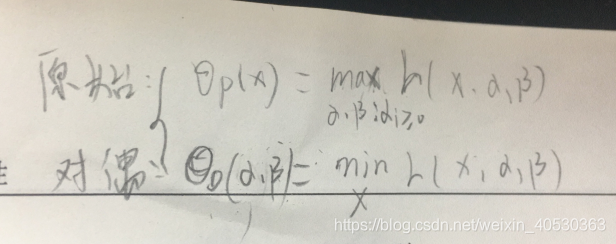

2)前提:满足定理C.3的假设部分称为凸优化问题,(这是原始问题与对偶问题有相同解的条件)。
KKT条件:
求取x*、a*、b*时该满足的条件


3)求解线性可分支持向量机的最优化问题(使用对偶算法)
至于为什么求解对偶问题会便于计算,手动解一下就能明白了。
首先原始最优化问题是(7.13~7.14),从式子可以看出需要求解的目标函数有w、b两个参数。当为了求解带有约束的它(凸优化问题)时需要构建拉格朗日函数(7.18),并引入拉格朗日乘子式,此时原始最优化问题是一个极小极大问题(最后求的仍然是以w、b为参数的函数,所以是7.13时的原问题)此时若是先求极大后求极小的话很难得到解,如下图。
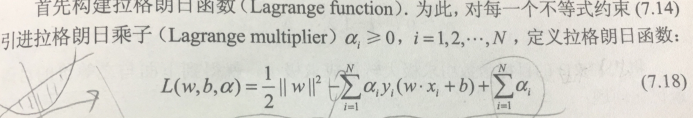
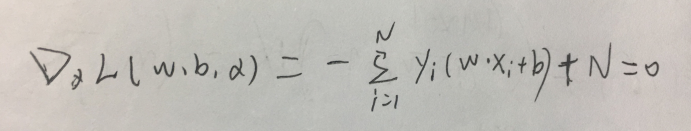
一个式子两个未知数。如此将其转化为对偶问题(极大极小问题)尤显重要了,这样的话先对w、b求偏导得到两个式子两个未知数,如图:

所以是否将原始问题要转化为对偶问题,一是,需要先查看它的参数分布情况。二是,求解过程中将其转化为对偶问题是因为要将其转化为满足凸优化问题的条件的情况,这样便于求解,也就是之前说过的凸优化函数更好求解(凸优化为何利于求解这里不作介绍)。(个人见解,请自行借鉴和思考)
之后将(7.19、7.20)带入(7.18)得到:
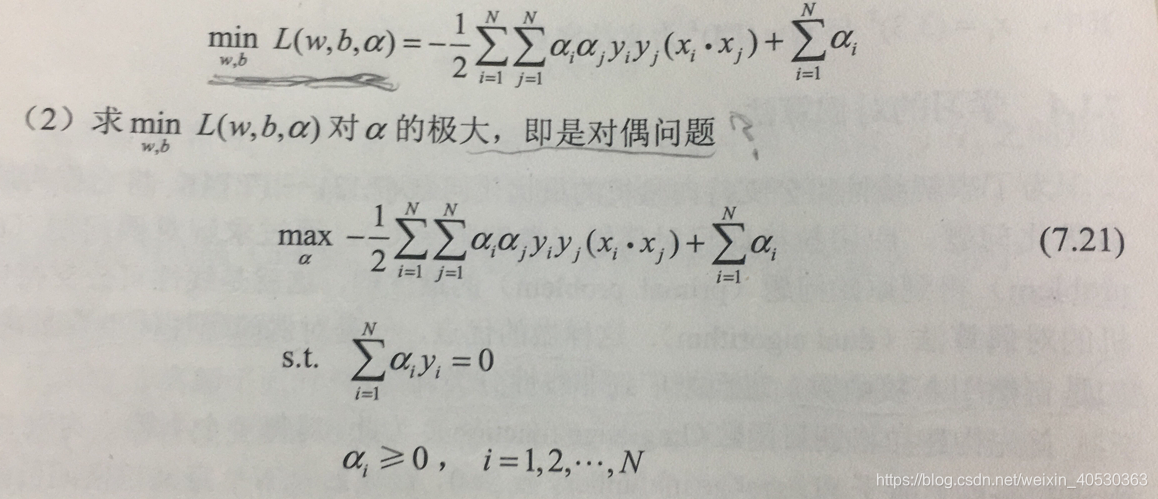
之后再将(7.21)的求极大转化为求极小(为了满足凸优化条件),得到下面与之等价的对偶问题
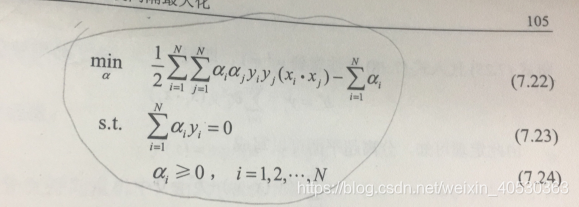
最后求得对偶问题的解a*,从而得到原始最优化问题的解w*、b*,如图:
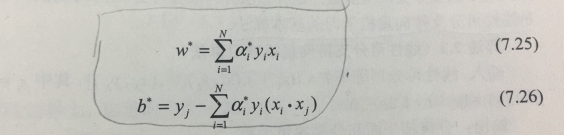
根据KKT条件所得(7.25、7.26)。

从而分离超平面可以写成:
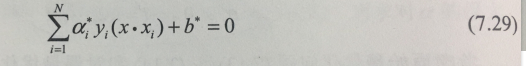
之后可以从KKT互补条件知道支持向量所在的超平面如下:
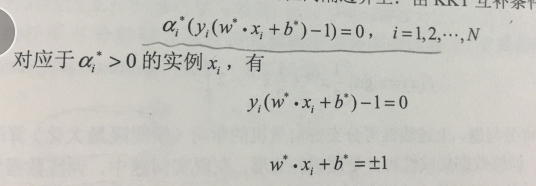





















 350
350

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








