本文详细介绍了树的基本概念，包括树的定义、术语和性质。接着探讨了树的存储结构，如双亲表示法、孩子表示法和二叉链表表示法。还讲解了树的遍历方法，如先根遍历和后根遍历。此外，重点阐述了二叉树的特性，包括满二叉树和完全二叉树，以及二叉树的遍历方法，如先序、中序、后序和层次遍历。文章还涉及了线索二叉树、森林转换为二叉树以及哈夫曼树的构造和编码。最后提到了并查集的概念及其基本操作。
目录
5.1 树的基本概念
5.1.1 树的定义
树是n个结点的有限集。当n=0时，称为空树。在任意一棵非空树中应满足：
- 有且仅有一个特定的称为根的结点。
- 当n>1时，其余结点可分为m个互不相交的有限集{T}，集合本身又是一棵树，并且称为根的子树。
显然，树的定义是递归的，即在树的定义中又用到了其自身，树是一种递归的数据结构。书作为一种逻辑结构，同时也是一种分层结构，具有以下两个特点：
- 树的根结点没有前驱，除根结点外的所有结点有且仅有一个前驱。
- 树中所有结点可以有零个或多个后继。
5.1.2 树的几种术语
- 树中一个结点的孩子个数称为该结点的度，树中最大度数称为树的度。
- 结点的深度是从根结点开始自顶向下逐层累加。
- 结点的高度是从叶结点开始自底向上逐层累加。
- 树的高度/深度是树中最大的深度/高度。
- 树的路径长度是指树根到每个结点的路径长的总和。
5.1.3 树的性质
- 树中结点数n等于所有结点的度数之和加1。
- 度为m的树(即m叉树)中第i层上至多有
个结点。
- 高度为h的m叉树至多有
个。
- 具有n个结点的m叉树最小高度为
。
5.2 树的表示
5.2.1 树的存储结构
1. 树的顺序存储---双亲表示法
//树的顺序存储法(双亲表示法)
#define MAX_Tree_Size 100//树的最多结点数
typedef struct{ //树的结点定义
Elemtype data;
int parent;
}PTNode;
typedef struct {// 树的类型定义
PTNode nodes[MAX_Tree_Size];
int n;//树的结点数
}PTree;
2. 孩子表示法
3. 二叉链表表示法---树的兄弟表示法
//树的兄弟表示法--二叉链表表示法
typedef struct CSNode {
Elemtype data;
struct CSNode* firstchild, * nextibling;//第一个孩子和右兄弟指针
}CSNode, * CSTree;
5.3 树的遍历
5.3.1 先根遍历
- 若树非空，访问根结点。
- 依次遍历子树并遵循先根后结点的原则。
对应二叉树的先序遍历：
- 先访问完根结点再依次访问左结点(树的孩子结点)和右结点(树的根结点)。
//树的先根遍历
void PreOrder(TreeNode* R)
{
if (R != NULL)
visit(R);
while (R还有下一个子树T)
PreOrder(T);
}5.3.2 后根遍历
- 先遍历同一结点不同孩子。
- 再访问双亲结点
对应二叉树中序遍历为：
- 访问完根结点(树双亲结点)再问右孩子(树的兄弟结点为根结点)。
- 访问完左子树(树的孩子结点)访问根结点。
//树的后根遍历
void PostOrder(TreeNode* R)
{
if (R != NULL) {
while (R还有下一个子树)
PostOrder(T);
visit(R);
}
}
5.4 二叉树
5.4.1 二叉树的定义
m=2的树即为二叉树，它有着所有有关树的定义；二叉树是有序树，若将左右子树颠倒，则成为另一颗完全不同的二叉树。即使树中的结点只有一棵子树，也要区分它是左子树还是右子树。二叉树可以为一颗空树。
满二叉树
一棵高度为h，且含有2^h-1个结点的树称为满二叉树。对于编号为i的结点，若有双亲，则其双亲若有左孩子，则左孩子为2i，右孩子为2i+1。
完全二叉树
每个结点在二叉树中的编号与满二叉树一一对应，则该树为完全二叉树。
- 若
，则结点i为分支结点，否则为叶子结点。
- 叶子结点只可能在层次最大的两层存在。
- 若n为奇数，则每个分支结点都有左孩子和右孩子；若n为偶数，则编号最大的分支结点只有左孩子没有右孩子。
5.4.2 二叉树的性质
- 非空二叉树上的叶子结点数等于度为2的结点数加1。
- 非空二叉树上第k层至多有
个结点。
- 高度为h的二叉树至多有
个结点。
5.5 二叉树的存储结构
5.5.1 二叉树的顺序存储结构
#define MAX_Size 100
typedef int Elemtype;
//二叉树的顺序存储结构
struct Tree_Node_1 {
Elemtype value;
bool isEmpty;
}Sqt[MAX_Size] ;
struct Tree_Node_2 {
Elemtype value;
bool isEmpty;
};
Tree_Node_2 Sqt[MAX_Size];//与上方等价
//初始化顺序树
void InitSqTree(Tree_Node_1 Sqt[])
{
for (int i = 0; i < MAX_Size; i++){
Sqt[i].value = 0;
Sqt[i].isEmpty = true;
}
}5.5.2 二叉树链式存储结构
//二叉树的链式存储结构
typedef struct BiTNode {
Elemtype data;
struct BiTNode* lchild, * rchild;
}BiTNode, * BiTree;
5.6 二叉树的遍历
二叉树的先序遍历(NLR)，中序遍历(LNR)，后序遍历(LRN)。其中序指的是根结点何时被访问。
5.6.1 先序遍历
//先序遍历(递归)
void preOrder_1(BiTree T)
{
visit(T);
preOrder_1(T->lchild);
preOrder_1(T->rchild);
}
//先序遍历(非递归)
void preOrder_2(BiTree T)
{
InitStack(S);
BiTNode* p = T;
while (p || isEmpty(S)) {
if (p) {
visit(p);
Push(S, p);
p = p->lchild;
}
else {
Pop(S);
p = p->rchild;
}
}
}
5.6.2 中序遍历
//中序遍历(递归)
void InOrder_1(BiTree T)
{
InOrder_1(T->lchild);
visit(T);
InOrder_1(T->rchild);
}
//中序遍历(非递归)
void InOrder_2(BiTree T)
{
InitStack(S);
BiTNode* p=T;
while (p || !isEmpty(S)) {
if (p) {//相当于InOrder_1(T->lchild)；
Push(S, p);
p = p->lchild;
}
//入栈到最后一个左结点，访问T后出栈并且入栈右结点
else {
Pop(S, p);
visit(p);
p = p->rchild;//相当于InOrder_1(T->rchild);
}
}
}
5.6.3 后序遍历
//后序遍历(递归)
void PostOrder_1(BiTree T)
{
PostOrder_1(T->lchild);
PostOrder_1(T->rchild);
visit(T);
}
5.6.4 层次遍历
//层次遍历
void LevelOrder(BiTree T)
{
InitQueue(Q);//辅助队列
BiTNode* p;//将要访问的结点
EnQueue(Q, T);
while (p)
{
DeQueue(Q,p);
visit(p);
if (p->lchild != NULL)
EnQueue(Q, p->lchild);
if(p->rchild!=NULL)
EnQueue(Q, p->rchild);
}
}5.6.5 由遍历序列构造二叉树
由二叉树的前序遍历和中序遍历可以唯一确定一棵二叉树。在前序遍历中第一个结点一定是二叉树的根结点；而在中序遍历中，根结点必然将中序序列分割成两个子序列；根据这两个子序列，在前序遍历中，左子序列的第一个结点是左子树的根结点；右子树同理；如此递归下去，便能唯一的确定这棵二叉树。
同理，由二叉树的后序序列和中序序列也可以唯一的确定一棵二叉树。
由二叉树的层次遍历和中序遍历也可以唯一确定一棵二叉树。层次遍历与前序或者后序不可以。
若只知道前序遍历和后序遍历，则无法确定一棵二叉树。
5.6.6 线索二叉树
规定：若无左子树，令lchild指向前驱；若无右子树，令rchild指向后继。下面以中序线索二叉树为例。
1. 线索二叉树结点结构
//线索二叉树结点结构
typedef struct ThreadNode {
Elemtype data;
struct ThreadNode* lchild, * rchild;//lchild指向前驱，rchild指向后继
int ltag, rtag;
}ThreadNode,* ThreadTree;
-
ltag=0时，lchild域指示结点的左孩子。
- ltag=1时，lchild域指示结点的前驱。
-
ltag=0时，lchild域指示结点的右孩子。
- ltag=1时，lchild域指示结点的后继。
2. 通过中序遍历对二叉树进行线索化
void InThread(ThreadTree &p,ThreadTree &pre)
{
if (p != NULL) {
InThread(p->lchild, pre);//遍历左子树
if (p->lchild == NULL) {
p->lchild = pre;
p->ltag = 1;
}
if (pre != NULL && pre->rchild == NULL) {
pre->rchild = p;
pre->rtag = 1;
}
pre = p;
InThread(p->rchild, pre);//遍历右子树
}
}
//通过中序遍历建立中序线索二叉树
void CreatInThread(ThreadTree T)
{
ThreadTree pre = NULL;
if (T != NULL) {
InThread(T, pre);
pre->rchild = NULL;//线索处理最后一个结点；
pre->rtag = 1;
}
}
3. 中序线索二叉树的遍历
//中序线索二叉树的遍历
//求中序序列下第一个结点
ThreadNode* Firstnode(ThreadNode* p)
{
while (p->ltag == 0)//最左下的结点
p = p->lchild;
return p;
}
//求中序线索二叉树结点p在中序序列下的后继
//根据rchild检索
ThreadNode* Nextnode(ThreadNode* p)
{
if (p->rtag == 0)
return Firstnode(p->lchild);
else
return p->rchild;
}
//不含头结点的中序线索二叉树的中序遍历
void InOrder(ThreadTree T)
{
for (ThreadNode* p = Firstnode(T); p != NULL; p = Nextnode(p))
visit(p);
}5.7 森林
森林是一颗或者多棵树的集合。
5.7.1 森林转换为二叉树
规则为左孩子右兄弟。由于根结点没有兄弟，所以对应的二叉树没有右子树。
5.8 哈夫曼树
5.8.1 哈夫曼树的定义
在许多应用中，树中结点被赋予一个表示某种意义的数值，称为结点的权值。从树根到任意结点的路径长度*该结点上权值的乘积，称为该结点的带权路径长度(WPL)，而WPL最小的二叉树称为哈夫曼树。
5.8.2 哈夫曼树的构造
- 将n个结点分别作为n棵仅含有一个结点的二叉树，构成森林F。
- 构造一个新结点，从F中选取两棵权值最小的结点作为新结点的左右子树，将新结点的权值置为两子树之和。
- 从F中删除刚才选出的两棵树，同时将新得到的树加入到F之中。
- 重复2.和3.步骤，直至剩下一棵树为止。
上述构造过程中可以看出哈夫曼树的特点：
- 每个初始结点最终都成为叶子结点。
- 构造过程中新建了n-1个结点，因此哈夫曼树的结点数为2n-1。
- 不存在度为1的结点。
5.8.3 哈夫曼编码
在数据通信中，若对每个字符用相等长度的二进制位表示，则称这种编码方式为固定长度编码。若允许对不同字符用不等长的二进制位表示，则成为可变长度编码。可变长度编码比固定长度编码要好得多，其特点是对频率高的字符赋以短编码，对频率低的字符赋以长编码，从而使字符的平均编码长度减短。
若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码。
由哈夫曼树的到哈夫曼编码是很自然的过程。首先构造出对应的哈夫曼树；此时所有字符结点都出现在叶子结点中。将字符编码解释为从根至该字符的路径上边标记的序列，边标记为0表示“转向左孩子”，标记为1表示“转向右孩子”。
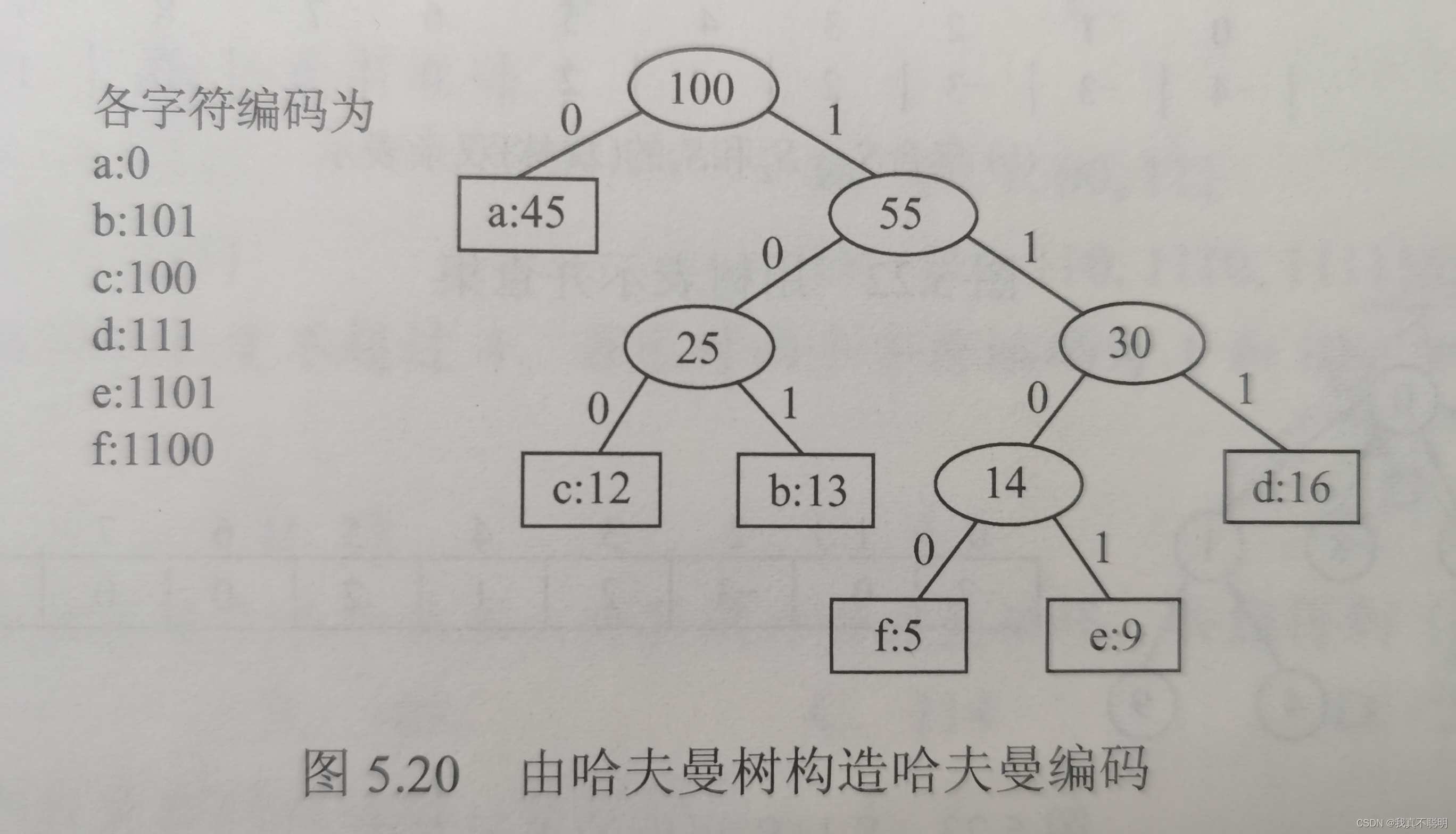
注意：0和1表示左孩子亦或右孩子没有明确规定；左右孩子的顺序是任意的。所以构造出的哈夫曼树并不唯一，但各哈夫曼树的WPL都是相同的。
5.8.4 并查集
并查集是一种简单的集合表示。通常用树或森林的双亲表示作为并查集的存储结构，每个子集合以一棵树表示。所有表示子集合的树，构成表示全集合的森林。通常用数组元素的下标代表元素名，用根结点的下标代表子集合名，根结点的双亲为负数。
1. 并查集的结构定义
/并查集的结构定义
#define Size 100
int UFSets[Size]; //集合元素数组
2. 并查集的初始化操作
//并查集的初始化操作
void Inital(int S[])
{
for (int i; i < Size; i++)
S[i] = -1;
}
3. Find操作
//并查集的Find操作
int Find(int S[],int x)//查找S中元素为x的所属集合并返回x的所属根结点
{
while (S[x] >= 0)
x = S[x];
return x;
}4. Union操作
//并查集的Union操作
int Union(int S[], int Root1, int Root2)//将ROOT1与ROOT2给Union成一个
{
if (Root1 == Root2)
return -9999;
S[Root2] = Root1;//将ROOT2连到ROOT1上
}
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
