matlab 矩阵除法简单记忆和使用

matlab 矩阵分左除右除,
先用一个小技巧记住两个除法符号 “”, “/”,
我称之为「除法棒」, 除法棒指向哪边, 哪边就是「除数矩阵」.
手持除法棒的始终是「被除数矩阵」, 这点在记忆时重要.

左除右除, 分别是左乘或右乘未知数的逆运算, 指向谁, 就等价于对哪一边求逆.
这个看起来混乱,
假如

A·B  =    C  

那么

B     =   A\C;   %(B =  inv(A)*C)
A     =   C/B;   %(A =  C*inv(A))

可以看到, C一会儿在左一会儿在右. 想要写代码时思路流畅, 其实掌握一个技巧就行:总是先写被除数 !!!
例:
求 (A·[?]=C): C 总是被除的那个不会变的, 只是矩阵中被除矩阵在除号的左边和右边意义不同.
因此,

1. 敲键盘 B= C
2. C 由未知数合成, 已知的值在左侧, 要除掉它. 除法棒指向未知数左侧, A\·
   3.B=A\C
   

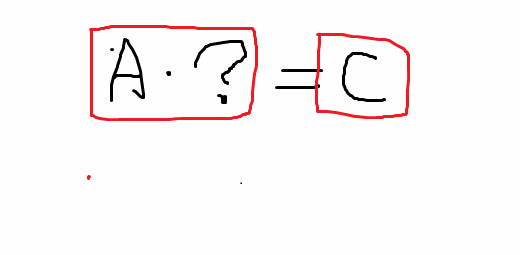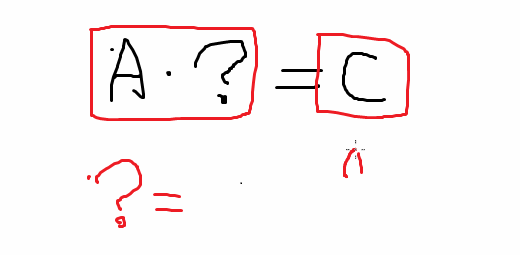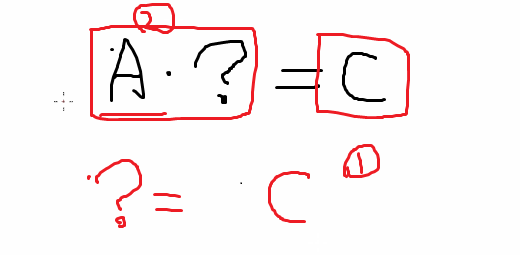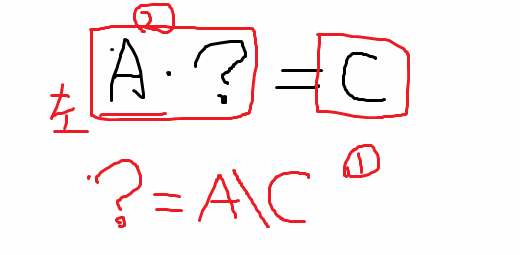
同样, 求 [?]*B=C:

1. 敲下 A= C
2. [?]*B就是C,C就是 [?]*B, 现在C要除掉已知的部分,就可以剩下未知的部分了.
3. A=C/B
   

说白了, 矩阵的除法就是做分解. C由左右两个矩阵合成而来, 要分解左边, 就用左除, 想除右边,就用右除.
矩阵的维度在整个过程中也保持一致. 在分解是什么样的, 分解之后还是什么样的.

matlab 中, 称上述的运算为 “分解”, 要比 “乘法的逆运算” 更为真实.
逆运算需要严格意义上的可逆, 而分解是可以不满秩的.

=====
最小二乘法:

matlab 中的除法可以在解有多个的时候用最小二乘法求解.
即「除数矩阵 B 」不可逆的时候. 猜一个值A, A*B 和 C 之间的差值最接近; (min(||xB-C||))或者(min(||Ax-C||))
第二种表述: 假如过定的情况下, 需要确定一个矩阵变换 B, 有无数种解, 求的是增加微小扰动, 却依然最能稳定输出的那个
这时候就要考虑维度的影响.

假设ABC三个矩阵维度分别是 4xN·Nx5=4x5

那么:

4xN \ (4x5) = Nx5
(4x5) / Nx5 = 4xN

可以看到, 除法棒指向哪侧, 哪侧就是维度, 是必须要对齐的那部分.
注意, 这里的 “维度” 和信号向量的 “维度” 的语义和而不同, 它只是计算时的一个定义.
假如你求过定时的传输矩阵 T , 搜集了很多 4 通道的数据,有 4xSamples 大小的的矩阵, 输出矩阵是 1xSamples, 那么 Samples 是做除法时的矩阵维度. T = 4 x Samples \ 1 x Samples

最后, 在左除右除不够用的时候, 再推荐lsq家族

x_b = lsqminnorm(A,b) %在 A\b的基础上增加了正则, 不仅使得使得 norm(Ax_b-b) 最小, 也 norm(X_b)最小. //最小 norm 某种意义上意味着条件数较小,秩更低, 不那么奇异.

图解:

为了使得优化工具也能为右除(系统识别)所用, 额外需要做一些转置:
对于xA=b
转置的定理: A'·x'=b'
因此求 A 就等价于(A'\b')', 或者 lsqminorm(A',b')', 可以看到, 被除数永远在第二个参数位置上.;